Average velocity

Average velocity

If a particle moves in one dimension, say for example along the x direction, then

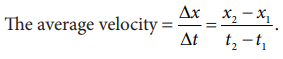
The average velocity is also a vector quantity. But in one dimension we have only two directions (positive and negative x direction), hence we use positive and negative signs to denote the direction.

The instantaneous velocity or velocity is defined as

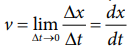
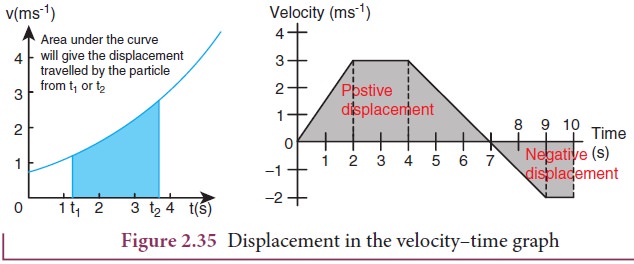
Graphically the slope of the position-time graph will give the velocity of the particle. At the same time, if velocity time graph is given, the distance and displacement are determined by calculating the area under the curve. This is explained below.

Since the left hand side of the integration represents the displacement travelled by the particle from time t1 to t2, the area under the velocity time graph will give the displacement of the particle. If the area is negative, it means that displacement is negative, so the particle has travelled in the negative direction. This is shown in the Figure 2.35 below.