Differential Calculus

DIFFERENTIAL CALCULUS

The Concept of a function

1) Any physical quantity is represented by a “function” in mathematics. Take the example of temperature T. We know that the temperature of the surroundings is changing throughout the day. It increases till noon and decreases in the evening. At any time “t” the temperature T has a unique value. Mathematically this variation can be represented by the notation ‘T(t)’ and it should be called “temperature as a function of time”. It implies that if the value of ‘t’ is given, then the function “T(t)” will give the value of the temperature at that time‘t’. Similarly, the position of a bus in motion along the x direction can be represented by x(t) and this is called ‘x' as a function of time’. Here ‘x’ denotes the x coordinate.

Example

Consider a function f(x) = x². Sometimes it is also represented as y = x². Here y is called the dependent variable and x is called independent variable. It means as x changes, y also changes. Once a physical quantity is represented by a function, one can study the variation of the function over time or over the independent variable on which the quantity depends. Calculus is the branch of mathematics used to analyse the change of any quantity.

If a function is represented by y = f(x), then dy/dx represents the derivative of y with respect to x. Mathematically this represents the variation of y with respect to change in x, for various continuous values of x.

Mathematically the derivative dy/dx is defined as follows

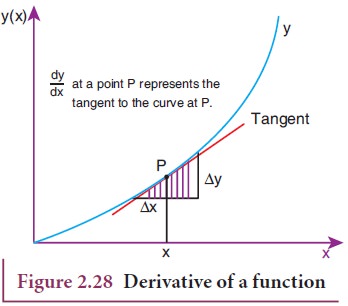
Graphically this is represented as shown in Figure 2.28.

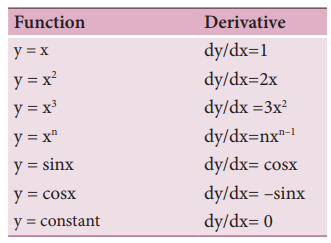
The table below shows the derivatives of some common functions used in physics

In physics, velocity, speed and acceleration are all derivatives with respect to time‘t’. This will be dealt with in the next section.

Solved Example Problems for Differential Calculus

Example 2.18

Consider the function y = x 2 . Calculate the derivative dy/dx using the concept of limit.

Solution

Let us take two points given by

These results are tabulated as shown below:

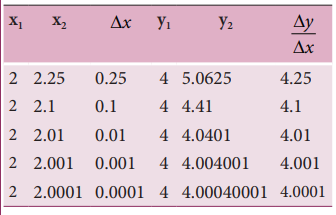
From the above table, the following inferences can be made.

Example 2.19

Find the derivative with respect to t, of the function x= A0 + A1t + A2 t2 where A0, A1 and A2 are constants.

Solution

Note that here the independent variable is ‘t’ and the dependent variable is ‘x’

The requived derivative is dx/dt = 0+ A1+2A2t

The second derivative is d2x/d2t = 2A2