Chapter: 11th Physics : UNIT 2 : Kinematics
Circular Motion
Circular
Motion
When
a point object is moving on a circular path with a constant speed, it covers
equal distances on the circumference of the circle in equal intervals of time.
Then the object is said to be in uniform circular motion. This is shown in
Figure 2.49.
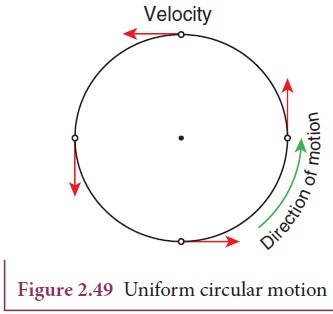
In
uniform circular motion, the velocity is always changing but speed remains the
same. Physically it implies that magnitude of velocity vector remains constant
and only the direction changes continuously.
If
the velocity changes in both speed and direction during the circular motion, we
get non uniform circular motion .
Centripetal acceleration
As
seen already, in uniform circular motion the velocity vector turns continuously
without changing its magnitude (speed), as shown in Figure 2.50.
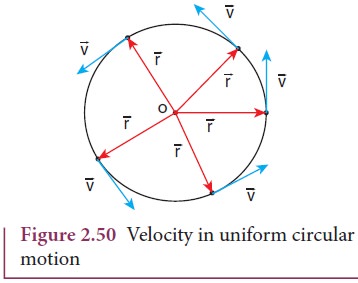
Note
that the length of the velocity vector (blue) is not changed during the motion,
implying that the speed remains constant. Even though the velocity is
tangential at every point in the circle, the acceleration is acting towards the
center of the circle. This is called centripetal acceleration. It always points
towards the center of the circle. This is shown in the Figure 2.51.

The
centripetal acceleration is derived from a simple geometrical relationship
between position and velocity vectors (Figure
2.48 or Figure 2.52).
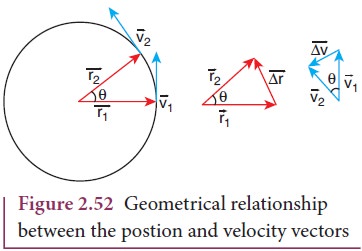

Here
the negative sign implies that ∆v
points radially inward, towards the center of the circle.
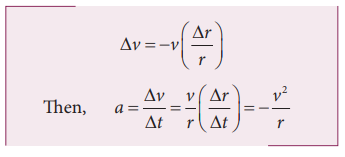
For
uniform circular motion v = ωr, where ω is the angular velocity of the particle about the center.
Then the centripetal acceleration can be written as

Non uniform circular motion
If
the speed of the object in circular motion is not constant, then we have
non-uniform circular motion. For example, when the bob attached to a string
moves in vertical circle, the speed of the bob is not the same at all time.
Whenever the speed is not same in circular motion, the particle will have both
centripetal and tangential acceleration as shown in the Figure 2.53.
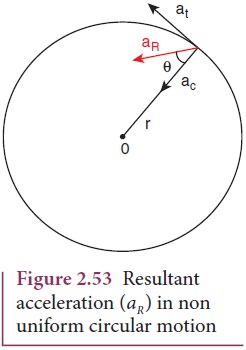
The
resultant acceleration is obtained by vector sum of centripetal and tangential
acceleration.

This
resultant acceleration makes an angle θ with the radius vector as shown in Figure 2.53.
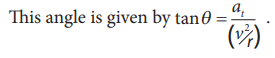
Kinematic Equations of circular motion
If
an object is in circular motion with constant angular acceleration α, we can
derive kinematic equations for this motion, analogous to those for linear
motion.
Let
us consider a particle executing circular motion with initial angular velocity ω0 . After a time interval t it attains a final angular velocity ω. During this time, it covers an angular displacement θ . Because of the change in angular
velocity there is an angular acceleration α.
The
kinematic equations for circular motion are easily written by following the
kinematic equations for linear motion in section 2.4.3
The
linear displacement (s) is replaced by the angular displacement (θ ).
The
velocity (v) is replaced by angular velocity (ω).
The
acceleration (a) is replaced by angular acceleration (α).
The
initial velocity (u) is replaced by the initial angular velocity (ω0 ).
By
following this convention, kinematic equations for circular motion are as in
the table given below .

Solved Example Problems for Circular Motion
Example 2.40
A particle moves in a circle of radius 10 m. Its linear speed is given by v = 3t where t is in second and v is in m s-1.
a) Find the centripetal and tangential acceleration at t = 2 s.
b) Calculate the angle between the resultant acceleration and the radius vector.
Solution
The linear speed at t = 2 s
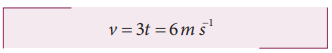
The centripetal acceleration at t = 2 s is
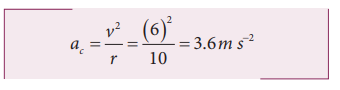
The angle between the radius vector with resultant acceleration is given by
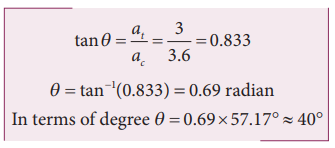
Example 2.41
A particle is in circular motion with an acceleration α = 0.2 rad s−2.
a) What is the angular displacement made by the particle after 5 s?
b) What is the angular velocity at t = 5 s?. Assume the initial angular velocity is zero.
Solution
Since the initial angular velocity is zero (ω0 = 0).
The angular displacement made by the particle is given by
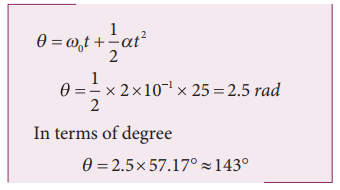
Related Topics