Chapter: 11th Physics : UNIT 2 : Kinematics
Equations of Uniformly Accelerated Motion by Calculus Method
Equations of Uniformly Accelerated Motion by Calculus Method
Consider an object moving in a straight line with uniform or constant acceleration ‘a’.
Let u be the velocity of the object at time t = 0, and v be velocity of the body at a later time t.
Velocity - time relation
(i) The acceleration of the body at any instant is given by the first derivative of the velocity with respect to time,
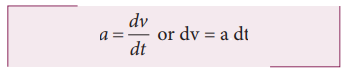
Integrating both sides with the condition that as time changes from 0 to t, the velocity changes from u to v. For the constant acceleration,

Displacement - time relation
(ii) The velocity of the body is given by the first derivative of the displacement with respect to time.
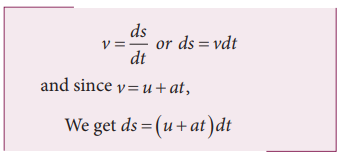
Assume that initially at time t = 0, the particle started from the origin. At a later time t, the particle displacement is s. Further assuming that acceleration is time-independent, we have
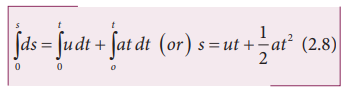
Velocity - displacement relation
(iii) The acceleration is given by the first derivative of velocity with respect to time.

Integrating the above equation, using the fact when the velocity changes from u2 to v2, displacement changes from 0 to s, we get
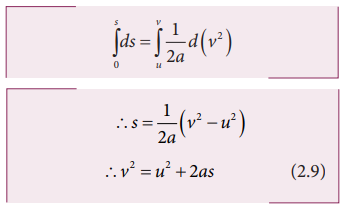
We can also derive the displacement s in terms of initial velocity u and final velocity v.
From the equation (2.7) we can write,
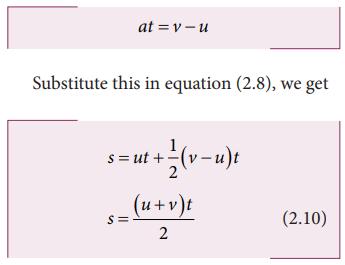
The equations (2.7), (2.8), (2.9) and (2.10) are called kinematic equations of motion, and have a wide variety of practical applications.
Kinematic equations
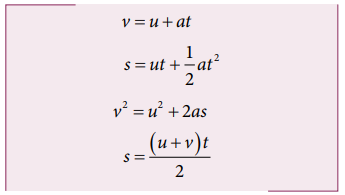
It is to be noted that all these kinematic equations are valid only if the motion is in a straight line with constant acceleration. For circular motion and oscillatory motion these equations are not applicable.
Solved Example Problems for Accelerated Motion
Example 2.31
A velocity–time graph is given for a particle moving in x direction, as below
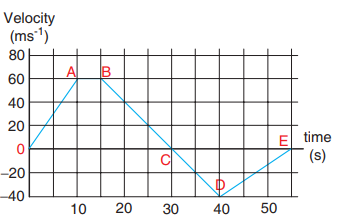
a) Describe the motion qualitatively in the interval 0 to 55 s .
b) Find the distance and displacement travelled from 0 s to 40 s .
c) Find the acceleration at t = 5 s and at t = 20 s
Solution
a) From O to A: (0 s to 10 s )
At t = 0 s the particle has zero velocity.
At t > 0, particle has positive velocity and moves in the positive x direction.
From 0 s to 10 s the slope (dv/dt) positive, implying the particle is accelerating. Thus the velocity increases during this time interval.
From A to B: (10 s to 15 s )
From 10 s to 15 s the velocity stays constant at 60 m s-1. The acceleration is 0 during this period. But the particle continues to travel in the positive x-direction.
From B to C : (15 s to 30 s )
From the 15 s to 30 s the slope is negative, implying the velocity is decreasing. But the particle is moving in the positive x direction. At t = 30 s the velocity becomes zero, and the particle comes to rest momentarily at t = 30 s .
From C to D: (30 s to 40 s )
From 30 s to 40 s the velocity is negative. It implies that the particle starts to move in the negative x direction. The magnitude of velocity increases to a maximum 40 m s-1
From D to E: (40 s to 55 s )
From 40 s to 55 s the velocity is still negative, but starts increasing from –40 m s-1 At t = 55 s the velocity of the particle is zero and particle comes to rest.
(b) The total area under the curve from 0 s to 40 s will give the displacement. Here the area from O to C represents motion along positive x–direction and the area under the graph from C to D represents the particle's motion along negative x–direction.
The displacement travelled by the particle from 0 s to 10 s = 1/2 × 10 × 60 = 300m
The displacement travelled from 10 s to 15 s = 60 × 5 = 300 m
The displacement travelled from 15 s to 30 s =1/2 × 15 × 60 = 450m
The displacement travelled from 30 s to 40 s = 1/2 × 10 × (-40) = -200m.
Here the negative sign implies that the particle travels 200 m in the negative x direction.

300 m + 300 m + 450 m − 200 m = +850 m.
Thus the particle's net displacement is along the positive x-direction.
The total distance travelled by the
particle from 0 s to 40 s = 300 + 300 + 450 + 200 = 1250 m.
(c) The acceleration is given by the slope in the velocity-time graph. In the first 10 seconds the velocity has constant slope (constant acceleration). It implies that the acceleration a is from v1 = 0 to v2 = 60 m s-1.
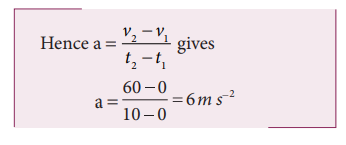
Next, the particle has constant negative slope from 15 s to 30 s . In this case v2=0 and v1=60m s-1. Thus the acceleration at t = 20 s is given by a = (0-60)/(30-15) = 4 m s-2. Here the negative sign implies that the particle has negative acceleration.
Example 2.32
If the position vector of the particle is given by 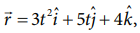 Find the
Find the
a. The velocity of the particle at t = 3 s
b. Speed of the particle at t = 3 s
c. acceleration of the particle at time t = 3 s
Solution

Example 2.33
An object is thrown vertically downward. What is the acceleration experienced by the object?
Solution
We know that when the object falls towards the Earth, it experiences acceleration due to gravity g = 9.8 m s-2 downward. We can choose the coordinate system as shown in the figure.
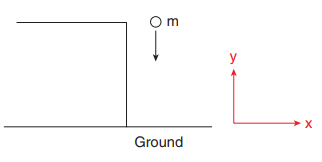
The acceleration is along the negative y direction.
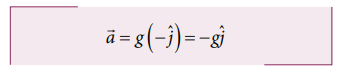
Related Topics