Solved Example Problem for Motion along One Dimension

Solved Example Problems for Average velocity

Example 2.25

A particle moves along the x-axis in such a way that its coordinates x varies with time 't' according to the equation x = 2 - 5t + 6t2. What is the initial velocity of the particle?

Solution

The negative sign implies that at t = 0 the velocity of the particle is along negative x direction.

Solved Example Problems for Relative Velocity in One and Two Dimensional Motion

Example 2.26

Suppose two cars A and B are moving with uniform velocities with respect to ground along parallel tracks and in the same direction. Let the velocities of A and B be 35 km h-1 due east and 40 km h-1 due east respectively. What is the relative velocity of car B with respect to A?

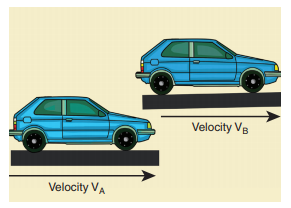
Solution

The relative velocity of B with respect to A, 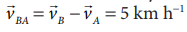due east

Similarly, the relative velocity of A with respect to B i.e., 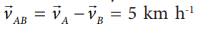due west.

Example 2.27

Suppose two trains A and B are moving with uniform velocities along parallel tracks but in opposite directions. Let the velocity of train A be 40 km h-1 due east and that of train B be 40 km h-1 due west. Calculate the relative velocities of the trains

Solution

Relative velocity of A with respect to B, vAB = 80 km h−1 due east

Thus to a passenger in train B, the train A will appear to move east with a velocity  of 80 km h−1

The relative velocity of B with respect to A, VBA = 80 km h−1  due west

To a passenger in train A, the train B will appear to move westwards with a velocity of 80 km h−1

Example 2.28

Consider two trains A and B moving along parallel tracks with the same velocity in the same direction. Let the velocity of each train be 50 km h-1 due east. Calculate the relative velocities of the trains

Solution

Similarly, relative velocity of A with respect to B i.e., vAB is also zero.

Thus each train will appear to be at rest with respect to the other.

Example 2.29

How long will a boy sitting near the window of a train travelling at 36 km h-1 see a train passing by in the opposite direction with a speed of 18 km h-1. The length of the slow-moving train is 90 m.

Solution

The relative velocity of the slow-moving train with respect to the boy is = (36 + 18) km h-1 = 54 km h-1 = = 54 × 5/18 ms-1 = 15 m s-1

Since the boy will watch the full length of the other train, to find the time taken to watch the full train:

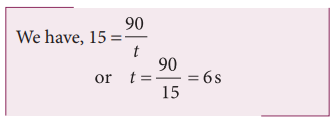
Example 2.30

A swimmer’s speed in the direction of flow of a river is 12 km h-1. Against the direction of flow of the river the swimmer’s speed is 6 km h-1. Calculate the swimmer’s speed in still water and the velocity of the river flow.

Solution

Let vs and vr , represent the velocities of the swimmer and river respectively with respect to ground.

When the river flow and swimmer move in the same direction, the net velocity of swimmer is 12 km p h-1.

Solved Example Problems for Accelerated Motion

Example 2.31

A velocity–time graph is given for a particle moving in x direction, as below

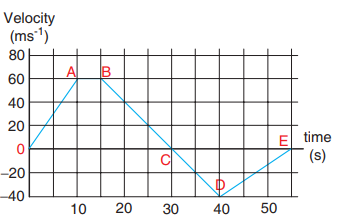
a) Describe the motion qualitatively in the interval 0 to 55 s .

b) Find the distance and displacement travelled from 0 s  to 40 s .

c) Find the acceleration at t = 5 s  and at t = 20 s

Solution

a) From O to A: (0 s  to 10 s )

At t = 0 s  the particle has zero velocity.

At t > 0, particle has positive velocity and moves in the positive x direction.

From 0 s   to 10 s   the slope (dv/dt) positive, implying the particle is accelerating. Thus the velocity increases during this time interval.

From A to B: (10 s  to 15 s )

From 10 s   to 15 s   the velocity stays constant at 60 m s-1. The acceleration is 0 during this period. But the particle continues to travel in the positive x-direction.

From B to C : (15 s  to 30 s )

From the 15 s   to 30 s   the slope is negative, implying the velocity is decreasing. But the particle is moving in the positive x direction. At t = 30 s   the velocity becomes zero, and the particle comes to rest momentarily at t = 30 s .

From C to D: (30 s  to 40 s )

From 30 s  to 40 s  the velocity is negative. It implies that the particle starts to move in the negative x direction. The magnitude of velocity increases to a maximum 40 m s-1

From D to E: (40 s  to 55 s )

From 40 s   to 55 s   the velocity is still negative, but starts increasing from –40 m s-1 At t = 55 s  the velocity of the particle is zero and particle comes to rest.

(b) The total area under the curve from 0 s  to 40 s  will give the displacement. Here the area from O to C represents motion along positive x–direction and the area under the graph from C to D represents the particle's motion along negative x–direction.

The displacement travelled by the particle from 0 s to 10 s = 1/2 × 10 × 60 = 300m

The displacement travelled from 10 s to 15 s = 60 × 5 = 300 m

The displacement travelled from 15 s to 30 s =1/2 × 15 × 60 = 450m

The displacement travelled from 30 s to 40 s = 1/2 × 10 × (-40) = -200m.

Here the negative sign implies that the particle travels 200 m in the negative x direction.

300 m + 300 m + 450 m − 200 m = +850 m.

Thus the particle's net displacement is along the positive x-direction.

The total distance travelled by the

particle from 0 s to 40 s = 300 + 300 + 450 + 200 = 1250 m.

(c) The acceleration is given by the slope in the velocity-time graph. In the first 10 seconds the velocity has constant slope (constant acceleration). It implies that the acceleration a is from v1 = 0 to v2 = 60 m s-1.

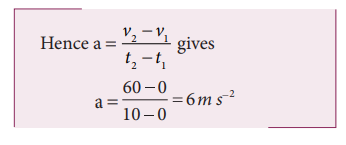
Next, the particle has constant negative  slope from 15 s to 30 s . In this case v2=0 and v1=60m s-1. Thus the acceleration at t = 20 s is given by a = (0-60)/(30-15) = 4 m s-2. Here the negative sign implies that the particle has negative acceleration.

Example 2.32

If the position vector of the particle is given by 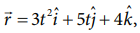Find the

a. The velocity of the particle at t = 3 s 

b. Speed of the particle at t = 3 s

c. acceleration of the particle at time t = 3 s

Solution

Example 2.33

An object is thrown vertically downward. What is the acceleration experienced by the object?

Solution

We know that when the object falls towards the Earth, it experiences acceleration due to gravity g = 9.8 m s-2 downward. We can choose the coordinate system as shown in the figure.

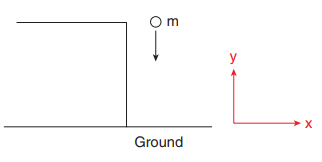
The acceleration is along the negative y direction.

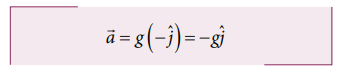
Solved Example Problems for motion under gravity: Case (1): A body falling from a height h

Example 2.34

An iron ball and a feather are both falling from a height of 10 m.

a) What are the time taken by the iron ball and feather to reach the ground?

b) What are the velocities of iron ball and feather when they reach the ground?

(Ignore air resistance and take g = 10 m s-2)

Solution

Since kinematic equations are independent of mass of the object, according to equation (2.8) the time taken by both iron ball and feather to reach the ground are the same. This is given by

Thus, both feather and iron ball reach ground at the same time.

By following equation (2.19) both iron ball and feather reach the Earth with the same speed. It is given by

Example 2.35

Is it possible to measure the depth of a well using kinematic equations?

Consider a well without water, of some depth d. Take a small object (for example lemon) and a stopwatch. When you drop the lemon, start the stop watch. As soon as the lemon touches the bottom of the well, stop the watch. Note the time taken by the lemon to reach the bottom and denote the time as t.

Since the initial velocity of lemon u = 0 and the acceleration due to gravity g is constant over the well, we can use the equations of motion for constant acceleration.

Since u = 0, s = d, a = g (Since we choose the y axis downwards), Then

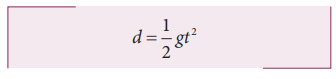
Substituting g = 9.8 m s-2 we get the depth of the well.

To estimate the error in our calculation we can use another method to measure the depth of the well. Take a long rope and hang the rope inside the well till it touches the bottom. Measure the length of the rope which is the correct depth of the well (dcorrect ). Then

What would be the reason for an error, if any?

Repeat  the  experiment  for  different masses and compare the result with dcorrect every time.

Solved Example Problems for motion under gravity: Case (2): A body thrown vertically upwards

Example 2.36

A train was moving at the rate of 54 km h-1 when brakes were applied. It came to rest within a distance of 225 m. Calculate the retardation produced in the train.

Solution

The final velocity of the particle v = 0

The initial velocity of the particle

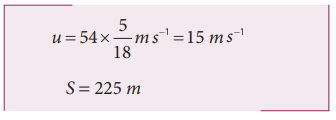
Retardation is always against the velocity of the particle.