Elementary Concepts of Vector Algebra

ELEMENTARY CONCEPTS OF VECTOR ALGEBRA

In physics, some quantities possess only magnitude and some quantities possess both magnitude and direction. To understand these physical quantities, it is very important to know the properties of vectors and scalars.

Scalar

It is a property which can be described only by magnitude. In physics a number of quantities can be described by scalars.

Examples

Distance, mass, temperature, speed and energy

Vector

It is a quantity which is described by both magnitude and direction. Geometrically a vector is a directed line segment which is shown in Figure 2.10. In physics certain quantities can be described only by vectors.

Examples

Force, velocity, displacement, position vector, acceleration, linear momentum and angular momentum

Magnitude of a Vector

The length of a vector is called magnitude of the vector. It is always a positive quantity. Sometimes the magnitude of a vector is also called ‘norm’ of the vector. For a vector , the magnitude or norm is denoted by || or simply ‘A’ (Figure 2.11).

Different types of Vectors

1. Equal vectors: Two vectors  and  are said to be equal when they have equal magnitude and same direction and represent the same physical quantity (Figure 2.12.).

a. Collinear vectors: Collinear vectors are those which act along the same line. The angle between them can be 0° or 180°.

i. Parallel Vectors: If two vectors  and  act  in the same direction along the same line or on parallel line, then the angle between them is 0⁰ (Figure 2.13).

ii. Anti-parallel vectors: Two vectors  and  are said to be anti-parallel when they are in opposite directions along the same line or on parallel lines. Then the angle between them is 180^o (Figure 2.14).

2. Unit vector: A vector divided by its magnitude is a unit vector. The unit vector for  is denoted by Aˆ (read as A cap or A hat). It has a magnitude equal to unity or one.

Thus, we can say that the unit vector specifies only the direction of the vector quantity.

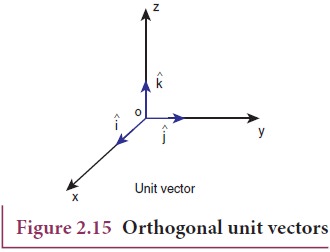
3. Orthogonal unit vectors: Let iˆ , jˆ and kˆ be three unit vectors which specify the directions along positive x-axis, positive y-axis and positive z-axis respectively. These three unit vectors are directed perpendicular to each other, the angle between any two of them is 90°. iˆ , jˆ and kˆ are examples of orthogonal vectors. Two vectors which are perpendicular to each other are called orthogonal vectors as is shown in the Figure 2.15

Addition of Vectors

Since vectors have both magnitude and direction they cannot be added by the method of ordinary algebra. Thus, vectors can be added geometrically or analytically using certain rules called ‘vector algebra’. In order to find the sum (resultant) of two vectors, which are inclined to each other, we use (i) Triangular law of addition method or (ii) Parallelogram law of vectors.

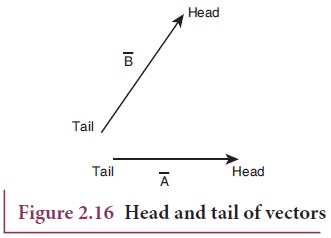
Triangular Law of a͢ddition method

Let us consider two vectors  and  as shown in Figure 2.16.

To find the resultant of the two vectors we apply the triangular law of addition as follows:

Represent the vectors  and  by the two adjacent sides of a triangle taken in the same order. Then the resultant is given by the third side of the triangle as shown in Figure 2.17.

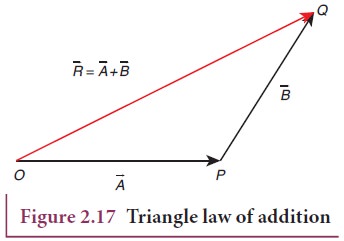
To explain further, the head of the first vector  is connected to the tail of the second vector . Let θ be the angle between  and . Then  is the resultant vector connecting the tail of the first vector  to the head of the second vector . The magnitude of  (resultant) is given geometrically by the length of  (OQ) and the direction of the resultant vector is the angle between  and . Thus we write = .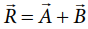

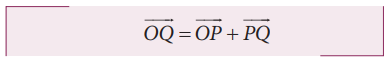
1. Magnitude of resultant vector

The magnitude and angle of the resultant vector are determined as follows.

From Figure 2.18, consider the triangle ABN, which is obtained by extending the side OA to ON. ABN is a right angled triangle.

From Figure 2.18

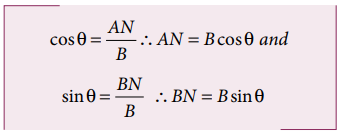
For ∆OBN, we have OB² = ON ² + BN ²

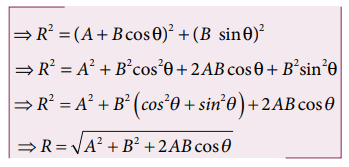
which is the magnitude of the resultant of  and 

2. Direction of resultant vectors:

If θ is the angle between  and  , then

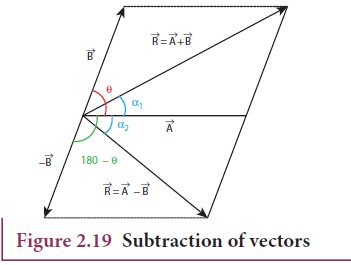
Subtraction of vectors

Since vectors have both magnitude and direction two vectors cannot be subtracted from each other by the method of ordinary algebra. Thus, this subtraction can be done either geometrically or analytically. We shall now discuss subtraction of two vectors geometrically using the Figure 2.19

For two non-zero vectors  and  which are inclined to each other at an angle θ, the difference  −  is obtained as follows. First obtain −  as in Figure 2.19. The angle between  and −  is 180-θ.

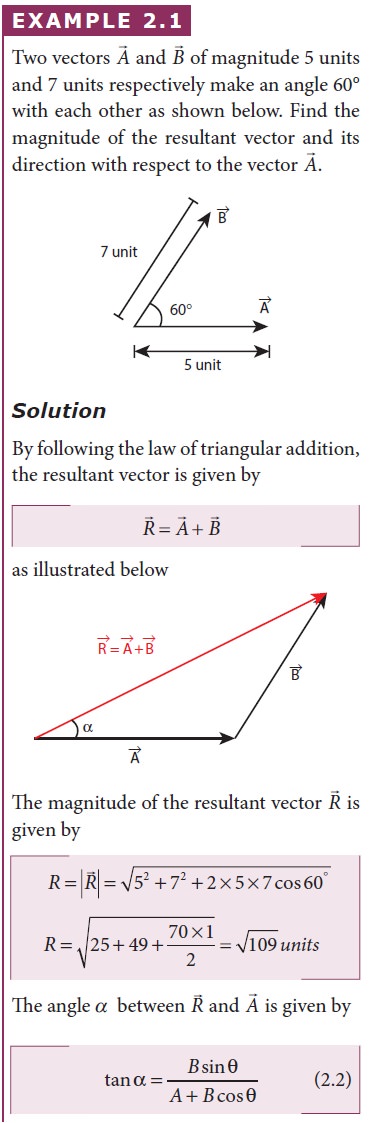
Solved Example Problem for Addition of Vectors

Solved Example Problem for Subtraction of vectors