Components of a Vector

COMPONENTS OF A VECTOR

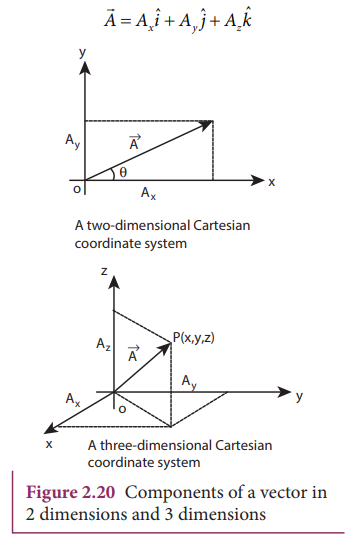
In the Cartesian coordinate system any vector  can be resolved into three components along x, y and z directions. This is shown in Figure 2.20.

Consider a 3-dimensional coordinate system. With respect to this a vector can be written in component form as

EXAMPLE 2.3

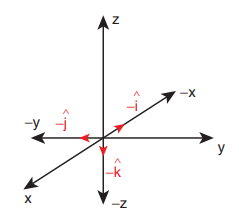
What are the unit vectors along the negative x–direction, negative y–direction, and negative z– direction?

Solution

The unit vectors along the negative directions can be shown as in the following figure.

Then we have:

The unit vector along the negative x direction = -iˆ

The unit vector along the negative y direction = -jˆ.

The unit vector along the negative z direction = -kˆ.

Vector addition using components

In the previous section we have learnt about addition and subtraction of two vectors using geometric methods. But once we choose a coordinate system, the addition and subtraction of vectors becomes much easier to perform.

The two vectors  and  in a Cartesian coordinate system can be expressed as

Then the addition of two vectors is equivalent to adding their corresponding x, y and z components.

Similarly the subtraction of two vectors is equivalent to subtracting the corresponding x, y and z components.

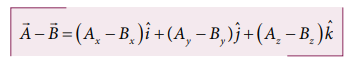
The above rules form an analytical way of adding and subtracting two vectors.