Introduction to Degrees and Radians

Introduction to Degrees and Radians

In measuring angles, there are several possible units used, but the most common units are degrees and radians. Radians are used in measuring area, volume, and circumference of circles and surface area of spheres.

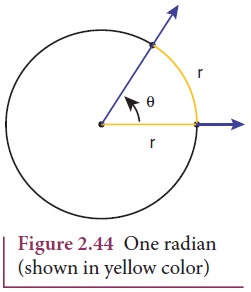
Radian describes the planar angle subtended by a circular arc at the center of a circle. It is defined as the length of the arc divided by the radius of the arc. One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. This is shown in the Figure 2.44.

Degree is the unit of measurement which is used to determine the size of an angle. When an angle goes all the way around in a circle, the total angle covered is equivalent to 360°. Thus, a circle has 360°. In terms of radians, the full circle has 2π radian.

Solved Example Problems for Degrees and Radians

Example 2.39

Calculate the angle θ subtended by the two adjacent wooden spokes of a bullock cart wheel is shown in the figure. Express the angle in both radian and degree.

Solution

The full wheel subtends 2π radians at the center of the wheel. The wheel is divided into 12 parts (arcs).

The angle subtended by two adjacent wooden spokes is 30 degree at the center.