with Solved Example Problems - Multiplication of Vector by a Scalar | 11th Physics : UNIT 2 : Kinematics
Chapter: 11th Physics : UNIT 2 : Kinematics
Multiplication of Vector by a Scalar
MULTIPLICATION OF VECTOR BY A SCALAR
A vector 
multiplied by a scalar λ results in another vector, λ. If λ is a
positive number then λ is also in the direction of . If λ
is a negative number, λ is in the opposite direction to the vector .
Scalar Product of Two Vectors
Definition
The
scalar product (or dot product) of two vectors is defined as the product of the
magnitudes of both the vectors and the cosine of the angle between them.
Thus
if there are two vectors and 
having an angle θ
between them, then their scalar product is defined as ⋅ = AB
cos θ. Here, A and B are magnitudes of and .
Properties
The
product quantity ⋅ is
always a scalar. It is positive if the angle between the vectors is acute
(i.e., < 90°) and negative if the angle between them is obtuse (i.e.
90°<θ< 180°).
The
work done is basically a scalar product between the force vector and the
displacement vector. Apart from work done, there are other physical quantities
which are also defined through scalar products.
The Vector Product of Two Vectors
Definition
The vector product or cross product
of two vectors is defined as another vector having a magnitude equal to the
product of the magnitudes of two vectors and the sine of the angle between
them. The direction of the product vector is perpendicular to the plane
containing the two vectors, in accordance with the right hand screw rule or
right hand thumb rule (Figure
2.22).
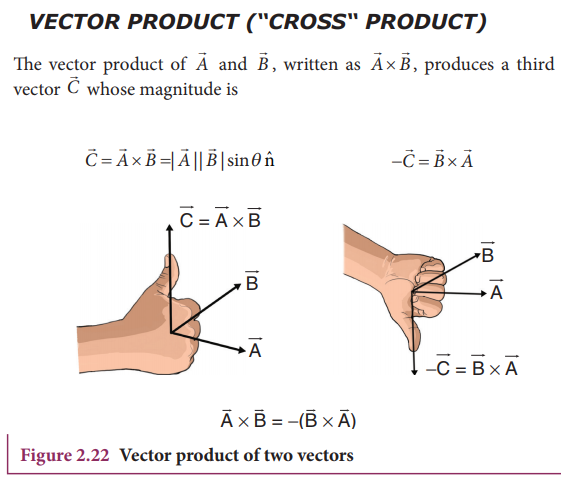
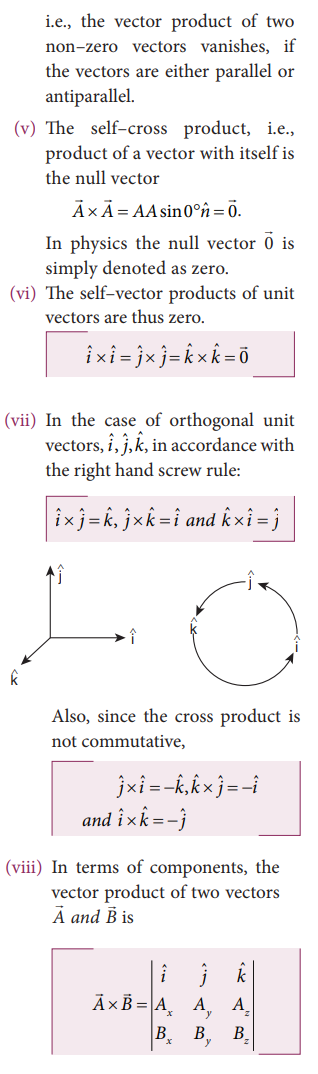
Properties of vector (cross) product.
A
number of quantities used in Physics are defined through vector products.
Particularly physical quantities representing rotational effects like torque,
angular momentum, are defined through vector products.
Properties of the components of vectors
If two vectors and are equal, then their individual components are also equal.
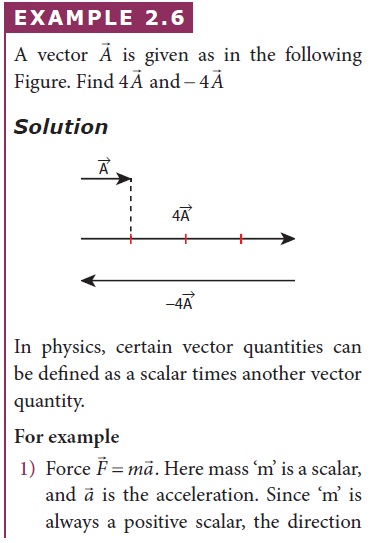
Solved Example Problems for Multiplication Of Vector By A Scalar
Solved Example Problems for Scalar Product of Two Vectors
Solved Example Problems for The Vector Product of Two Vectors
Solved Example Problems for Properties of the components of vectors
Related Topics