Quantitative and Qualitative Aspects of Voltammetry

Quantitative and Qualitative Aspects of Voltammetry

Earlier we described a voltammogram as the electrochemical equivalent of a spec- trum in spectroscopy. In this section we consider how quantitative and qualitative information may be extracted from a voltammogram. Quantitative information is obtained by relating current to the concentration of analyte in the bulk solution. Qualitative information is obtained from the voltammogram by extracting the standard-state potential for the redox reaction. For simplicity we only consider voltammograms similar to that shown in Figure 11.33a.

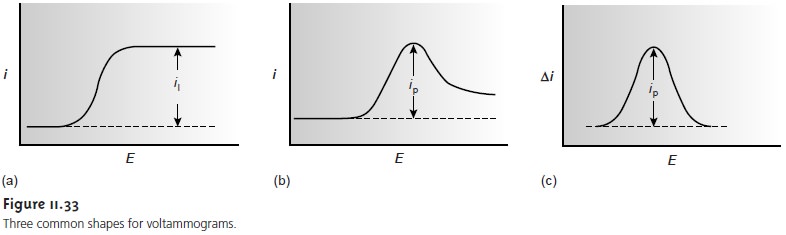
Determining Concentration 

Let’s assume that the redox reaction at the working electrode is

O+ ne– < = = = = > R    ……………11.34

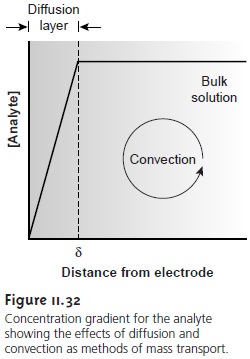
and that initially only O is present in the bulk solution. The current is determined by the rate at which O diffuses through the fixed diffusion layer (see Figure 11.32), and is given by equation 11.33, or

i = K_O([O]_bulk – [O]_x=0)    ……………11.35

where K_O is a constant equal to nFAD_O/ δ. When the limiting current is reached, the concentration of O at the electrode surface is zero, and this equation simplifies to

i_lim = K_O[O]_bulk    ……………11.36

Thus, the limiting current, i_lim, is a linear function of the concentration of O in bulk solution, and a quantitative analysis is possible using any of the standardization methods. Equations similar to equation 11.35 can be devel- oped for other forms of voltammetry, in which peak currents are related to the ana- lyte’s concentration in bulk solution.

Determining the Standard-State Potential 

To extract the standard-state potential, or formal potential, for reaction 11.34 from a voltammogram, it is necessary to rewrite the Nernst equation

                         11.37

in terms of current instead of the concentration of O and R. Substituting equation 11.36 into equation 11.35 and rearranging gives

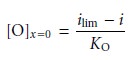                                                   11.38

To derive a similar equation for the concentration of R at the electrode surface we note that

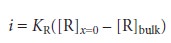
Since the concentration of R in bulk solution is zero, this equation simplifies to

i = K_R[R]_x=0

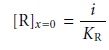                 11.38

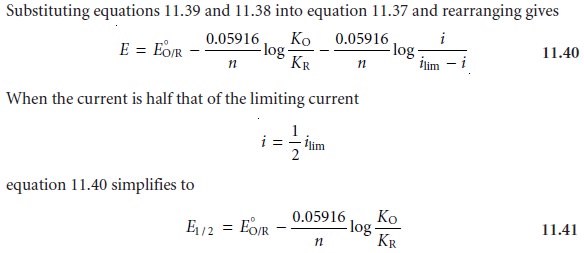
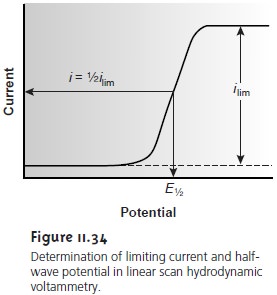
where E_1/2 is the half-wave potential (Figure 11.34). If K_O is approximately equal to K_R, which is often the case, then the half-wave potential is equal to the standard-state potential. Note that equation 11.41 is only valid if the redox reaction is electrochemically reversible. Voltammetric techniques giv- ing peak potentials also can be used to determine a redox reaction’s standard- state potential.