Current in Voltammetry

Current in Voltammetry

When an analyte is oxidized at the working electrode, a current passes electrons through the external electric circuitry to the auxiliary electrode, where reduc- tion of the solvent or other components of the solution matrix occurs. Reducing an analyte at the working electrode requires a source of electrons, generating a current that flows from the auxiliary electrode to the cathode. In either case, a current resulting from redox reactions at the working and auxiliary electrodes is called a faradaic current. In this section we consider the factors affecting the magnitude of this faradaic current, as well as the source of any nonfaradaic currents.

Sign Conventions 

Since the reaction of interest occurs at the working electrode, the classification of current is based on this reaction. A current due to the analyte’s reduction is called a cathodic current and, by convention, is considered positive. Anodic currents are due to oxidation reactions and carry a negative value.

Influence of Applied Potential on the Faradaic Current 

As an example, let’s con- sider the faradaic current when a solution of Fe(CN) ₆3– is reduced to Fe(CN) ₆ 4– at

the working electrode. The relationship between the concentrations of Fe(CN) ₆3–,

Fe(CN) ₆4–, and the potential of the working electrode is given by the Nernst equa- tion; thus

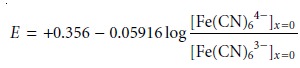
where +0.356 is the standard-state potential for the Fe(CN)₆3–/Fe(CN)₆4– redox couple, and x = 0 indicates that the concentrations of Fe(CN)₆3– and Fe(CN)₆4– are those at the surface of the electrode. Surface concentrations are used instead of bulk concentrations since the equilibrium position for the redox reaction

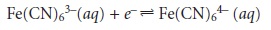
can only be established electrochemically at the electrode’s surface.

Let’s assume that we have a solution for which the concentration of Fe(CN)₆3– is 1.0 mM and in which Fe(CN) ₆4– is absent. A ladder diagram for this redox example is shown in Figure 11.29. If a potential of +0.530 V is applied to the working electrode, the concentrations of Fe(CN)₆3– and Fe(CN)₆4– at the surface of the elec- trode are unaffected, and no faradaic current is observed. Switching the potential to +0.356 V, however, requires that

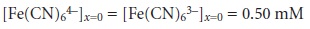
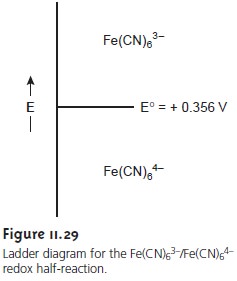
Which is only possible if a portion of the Fe(CN)₆³– at the electrode surface is re- duced to Fe(CN)₆⁴–. If this was all that occurred after the potential was applied, the result would be a brief surge of faradaic current that would quickly return to zero. However, although the concentration of Fe(CN)₆4– at the electrode surface is 0.50 mM, its concentration in the bulk of solution is zero. As a result, a concentration gradient exists between the solution at the electrode surface and the bulk solution. This concentration gradient creates a driving force that transports Fe(CN)₆4– away from the electrode surface (Figure 11.30). The subsequent decrease in the concen- tration of Fe(CN)₆4– at the electrode surface requires the further reductionof E

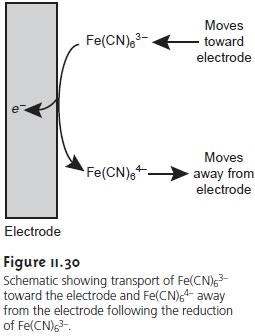
 Fe(CN) ₆3–, as well as its transport from bulk solution to the electrode surface. Thus, a faradaic current continues to flow until there is no difference between the concen- trations of Fe(CN) ₆3– and Fe(CN) ₆4– at the electrode surface and their concentrations in the bulk of solution.*

Although the applied potential at the working electrode determines if a faradaic current flows, the magnitude of the current is determined by the rate of the result- ing oxidation or reduction reaction at the electrode surface. Two factors contribute to the rate of the electrochemical reaction: the rate at which the reactants and prod- ucts are transported to and from the surface of the electrode, and the rate at which electrons pass between the electrode and the reactants and products in solution.

Influence of Mass Transport on the Faradaic Current 

There are three modes of mass transport that influence the rate at which reactants and products are trans- ported to and from the electrode surface: diffusion, migration, and convection. Dif- fusion from a region of high concentration to a region of low concentration occurs whenever the concentration of an ion or molecule at the surface of the electrode is different from that in bulk solution. 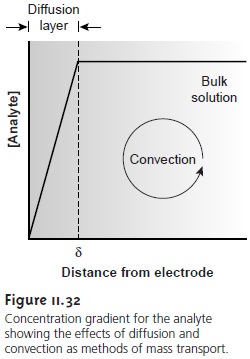When the potential applied to the working electrode is sufficient to reduce or oxidize the analyte at the electrode surface, a con- centration gradient similar to that shown in Figure 11.31 is established. The volume of solution in which the concentration gradient exists is called the diffusion layer. Without other modes of mass transport, the width of the diffusion layer, δ, in- creases with time as the concentration of reactants near the electrode surface de- creases. The contribution of diffusion to the rate of mass transport, therefore, is time-dependent.

Convection occurs when a mechanical means is used to carry reactants toward the electrode and to remove products from the electrode. The most common means of convection is to stir the solution using a stir bar. Other methods include rotating the electrode and incorporating the electrode into a flow cell.

The final mode of mass transport is migration, which occurs when charged particles in solution are attracted or repelled from an electrode that has a positive or negative surface charge. Thus, when the electrode is positively charged, negatively charged particles move toward the electrode, while positively charged particles move toward the bulk solution. Unlike diffusion and convection, migration only af- fects the mass transport of charged particles.

The flux of material to and from the electrode surface is a complex function of all three modes of mass transport. In the limit in which diffusion is the only signifi- cant means for the mass transport of the reactants and products, the current in a voltammetric cell is given by

                             11.33

where n is the number of electrons transferred in the redox reaction, F is Faraday’s constant, A is the area of the electrode, D is the diffusion coefficient for the reactant or product, C_bulk and C_x=0 are the concentration of the analyte in bulk solution and at the electrode surface, and δ is the thickness of the diffusion layer.

For equation 11.33 to be valid, convection and migration must not interfere with the formation of a diffusion layer between the electrode and the bulk of solu- tion. Migration is eliminated by adding a high concentration of an inert supporting electrolyte to the analytical solution. Ions of similar charge are equally attracted or repelled from the surface of the electrode and, therefore, have an equal probability of undergoing migration. The large excess of inert ions, however, ensures that few reactant and product ions will move as a result of migration. Although convection may be easily eliminated by not physically agitating the solution, in some situations it is desirable either to stir the solution or to push the solution through an electro- chemical flow cell. Fortunately, the dynamics of a fluid moving past an electrode re- sults in a small diffusion layer, typically of 0.001 – 0.01-cm thickness, in which the rate of mass transport by convection drops to zero (Figure 11.32).

Influence of the Kinetics of Electron Transfer on the Faradaic Current 

The rate of mass transport is one factor influencing the current in a voltammetric experiment. The ease with which electrons are transferred between the electrode and the reac- tants and products in solution also affects the current. When electron transfer ki- netics are fast, the redox reaction is at equilibrium, and the concentrations of reac- tants and products at the electrode are those specified by the Nernst equation. Such systems are considered electrochemically reversible. In other systems, when electron transfer kinetics are sufficiently slow, the concentration of reactants and products at the electrode surface, and thus the current, differ from that predicted by the Nernst equation. In this case the system is electrochemically irreversible.

Nonfaradaic Currents 

Faradaic currents result from a redox reaction at the elec- trode surface. Other currents may also exist in an electrochemical cell that are unre- lated to any redox reaction. These currents are called nonfaradaic currents and must be accounted for if the faradaic component of the measured current is to be determined.

The most important example of a nonfaradaic current occurs whenever the electrode’s potential is changed. In discussing migration as a means of mass trans- port, we noted that negatively charged particles in solution migrate toward a posi- tively charged electrode, and positively charged particles move away from the same electrode. When an inert electrolyte is responsible for migration, the result is a structured electrode–surface interface called the electrical double layer, or EDL, the exact structure of which is of no concern in the context of this text. The movement of charged particles in solution, however, gives rise to a short-lived, nonfaradaic charging current. Changing the potential of an electrode causes a change in the structure of the EDL, producing a small charging current.

Residual Current 

Even in the absence of analyte, a small current inevitably flows through an electrochemical cell. This current, which is called the residual current, consists of two components: a faradaic current due to the oxidation or reduction of trace impurities, and the charging current.