Chapter: Modern Analytical Chemistry: Electrochemical Methods of Analysis
Quantitative Applications - Potentiometric Methods of Analysis
Quantitative
Applications
The potentiometric determination of an analyte’s concentration is one of the most
common quantitative analytical techniques. Perhaps the
most frequently employed, routine quantitative
measurement is the potentiometric determination of a solu- tion’s pH, a technique
considered in more detail in the following
discussion. Other areas in which potentiometric applications are important include clinical chemistry, environmental chemistry, and
potentiometric titrations. Before considering these applications, however, we must first
examine more closely
the relationship between cell potential and the analyte’s concentration, as well as methods for standardizing
potentiometric measurements.
Activity Versus Concentration
In describing metallic and membrane indicator elec-
trodes, the Nernst equation relates
the measured cell
potential to the
concentration of analyte. In writing the
Nernst equation, we often ignore
an important detail—the potential of an electrochemical cell is a function of activity, not concen-
tration. Thus, the
Nernst equation for a metallic
electrode of the first
kind is more appropriately written
as
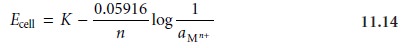
where aMn+ is the activity of the metal
ion. As described, the activity
of an ion is equal to the product of its concentration,
[Mn+], and a matrix-dependent activity coefficient, γMn+.

Substituting equation 11.15 into equation 11.14 and rearranging
gives
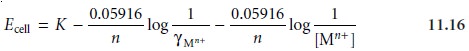
Equation 11.16 can
be solved for
the metal ion’s
concentration if its
ac- tivity coefficient is known. This presents a serious complication since the activity coefficient may be difficult to determine. If,
however, the standards and samples have an identical matrix, then γMn+ remains constant, and equation 11.16
simplifies to
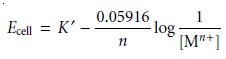
where K’ includes the
activity coefficient.
Quantitative Analysis Using External Standards
To determine the concentration of analyte in a sample, it is necessary to standardize the electrode. If the electrode’s response obeys the Nernst equation, then only the constant K need be determined, and standardizing with a single ex- ternal standard is possible. Since small deviations from the ideal “Nerstian” slope of ±RT/nF or ±RT/zF are frequently observed, standardization is usually accom- plished using two or more external standards.
In most quantitative analyses we are
interested in determining the concen-
tration, not the activity, of the analyte. As noted earlier, however, the electrode’s response is a function of the analyte’s activity. In the absence of interferents,
a calibration curve
of potential versus
activity is a straight line.
A plot of poten- tial versus concentration, however, may be curved at higher concentrations
of analyte due to changes
in the analyte’s activity coefficient. A curved calibra- tion curve may still
be used to determine the
analyte’s concentration if the stan- dard’s matrix matches that of the sample. When the exact composition of the sample matrix is unknown,
which often is the case, matrix matching becomes
impossible.
Another
approach
to
matrix
matching, which does not rely on knowing
the
exact
composition of the sample’s matrix, is to add a high concentration
of inert electrolyte to all samples and standards. If the concentration of added
electrolyte is sufficient, any difference between the sample’s matrix and that of the standards
becomes trivial, and the activity coefficient remains essentially constant. The solution
of inert electrolyte added to the sample and standards
is called a total ionic strength adjustment buffer (TISAB).

Quantitative Analysis Using the Method of Standard Additions
Because of the dif- ficulty of maintaining a constant matrix
for samples and standards, many quantita-
tive potentiometric methods
use the method of standard
additions. A sample of vol- ume,
VX, and
analyte concentration, CX, is transferred to a sample
cell, and the potential, (Ecell)X, measured. A standard addition
is made by adding a small volume, VS, of a standard containing a known concentration of analyte, CS, to the sample, and the potential, (Ecell)S, measured. Provided that VS is significantly smaller
than VX, the change in sample matrix is ignored,
and the analyte’s activity coefficient re- mains constant. Example
11.7 shows how a one-point standard addition can be
used to determine the concentration of an analyte.


Free Ions Versus Complexed Ions
In discussing the F– ion-selective electrode, we noted that the membrane potential
is influenced by the concentration of F–, but not
the concentration of HF. An analysis
for fluoride, therefore,
is pH-dependent. Below a pH of approximately 4, fluoride is present predominantly as HF, and a
quantitative analysis for
total fluoride is impossible. If the pH is increased to greater than 4, however, the equilibrium
HF(aq)+ H2O(l) < = = = = > H3O+(aq)+ F–(aq)
shifts to the right, and a quantitative analysis for total
fluoride is possible.
Most potentiometric electrodes are selective for
only the free,
uncomplexed analyte and do not respond
to complexed forms of the analyte. Solution
condi- tions, therefore, must be carefully
controlled if the purpose of the analysis
is to de- termine the analyte’s total concentration. On the other
hand, this selectivity pro- vides a significant advantage over other quantitative methods
of analysis when it is necessary to determine the concentration of free ions. For example,
calcium is present in urine both
as free Ca2+ ions and
as protein-bound Ca2+ ions. If a urine sample is analyzed by atomic absorption spectroscopy, the signal is proportional to the total concentration of Ca2+, since
both free and bound calcium
are atomized. Analysis with a Ca2+ ISE, however,
gives a signal
that is a function of only free Ca2+ ions since
the protein-bound ions cannot interact
with the electrode’s membrane.
Representative Method
Ion-selective electrodes find application in numerous quantitative analyses, each of which has its own unique considerations. The following pro- cedure for the analysis of fluoride in toothpaste provides an instructive example.
Measurement of pH
With the
availability of inexpensive glass pH electrodes and pH meters, the determination of pH has become one of the most frequent
quantita- tive analytical measurements. The potentiometric determination of pH, however,
is not without complications, several of which
are discussed in this section.
One complication is the meaning
of pH.
The conventional definition of pH as presented in most introductory texts is
pH = –log [H+] ………..11.17
The pH of a solution, however, is defined
by the response of an electrode to the H+ ion
and, therefore, is a measure
of its activity.
pH = –log(aH+)
………..11.18
Calculating the pH of a solution using
equation 11.17 only approximates the true
pH. Thus, a solution of 0.1 M HCl has a calculated pH of 1.00 using equation
11.17, but an actual
pH of 1.1 as defined
by equation 11.18.8 The difference between the two values
occurs because the activity coefficient for H+ is not unity in a matrix
of 0.1 M HCl. Obviously the true pH of a solution is affected by the composition of its matrix. As an extreme
example, the pH of 0.01
M HCl in 5 m LiCl is 0.8, a value
that is more acidic than
that of 0.1
M HCl!
A second complication in measuring pH results from uncertainties in the rela- tionship between potential and
activity. For a glass membrane electrode, the cell
po- tential, EX, for a solution
of unknown pH is given
as
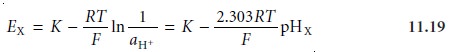
where K includes the potential of the reference
electrode, the asymmetry
potential of the glass
membrane and any liquid junction
potentials in the electrochemical cell. All the contributions to K are subject
to uncertainty and
may change from
day to day, as well as between electrodes. For this reason
a pH electrode must be calibrated
using a standard buffer of known pH. The cell potential for the standard, ES, is
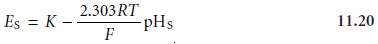
where pHS is the pH of the standard. Subtracting
equation 11.20 from equation 11.19 and
solving for pH gives
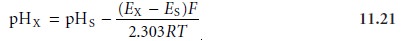
which is the operational definition of pH adopted
by the International Union of Pure
and Applied Chemistry.*
Calibrating the electrode presents a third
complication since a standard with
an accurately known activity
for H+ needs to be used.
Unfortunately, it is not possible to calculate rigorously the activity of a single
ion. For this reason pH electrodes are calibrated using a standard
buffer whose composition is chosen such that the de-
fined pH is as close as possible
to that given by equation
11.18. Table 11.6 gives pH values
for several primary
standard buffer solutions accepted by the National Insti- tute of Standards and Technology.

A pH electrode is normally standardized using two buffers: one near a pH of 7
and one that is more
acidic or basic
depending on the
sample’s expected pH.
The pH electrode is immersed in the first
buffer, and the
“standardize” or “calibrate” control is adjusted until
the meter reads
the correct pH. The electrode is placed in the
second buffer, and the “slope”
or “temperature” control
is adjusted to the-
buffer’s pH. Some pH meters are equipped with a temperature compensation fea- ture, allowing the pH meter to correct the measured pH for any change in tempera-
ture. In this case a thermistor is placed in the sample and connected
to the pH meter. The “temperature” control is set to the solution’s temperature, and the pH meter
is calibrated using
the “calibrate” and “slope” controls. If a change
in the sample’s temperature is indicated by the thermistor, the pH meter
adjusts the slope of the calibration based
on an assumed Nerstian response of 2.303RT/F.
Clinical Applications
Perhaps the area in which ion-selective electrodes receive the widest use is in clinical analysis, where their selectivity for the analyte in a complex matrix provides a significant advantage over many other analytical methods. The most common analytes are electrolytes, such as Na+, K+, Ca2+, H+, and Cl–, and dis- solved gases, such as CO2. For extracellular fluids, such as blood and urine, the analy- sis can be made in vitro with conventional electrodes, provided that sufficient sample is available. Some clinical analyzers place a series of ion-selective electrodes in a flow cell, allowing several analytes to be monitored simultaneously.
Standards, samples,
and rinse solutions are pumped through the flow cell and across the surface
of the electrodes. For smaller volumes
of sample the analysis can be conducted
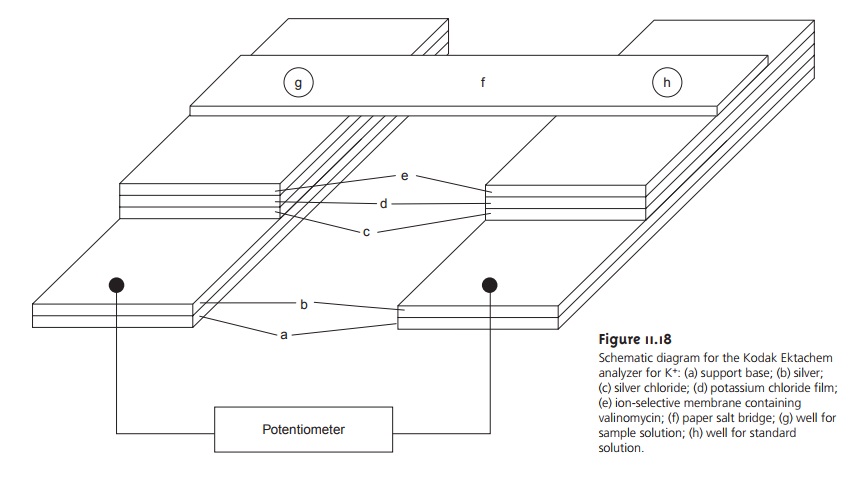
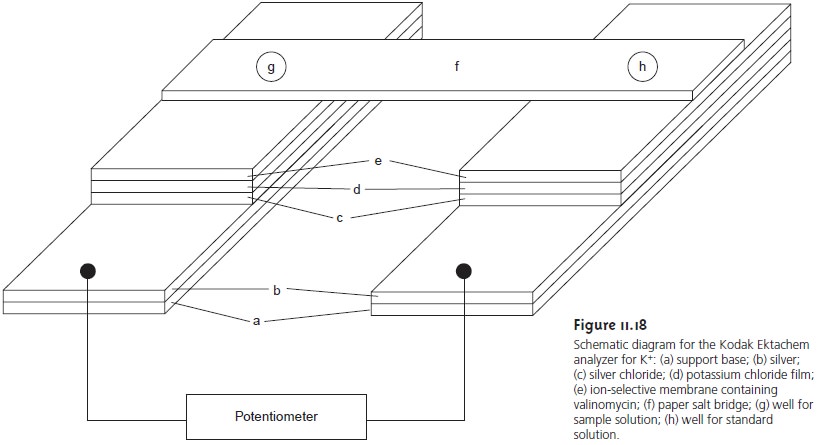
using dis- posable ion-selective systems, such as the Kodak
Ektachem analyzer for K+ shown in Figure 11.18. The analyzer consists
of separate electrodes for the sample and refer- ence solutions. Each electrode is constructed from
several thin films,
consisting of a Ag/AgCl reference electrode, a salt bridge
and an ion-selective membrane, deposited on a support base.
The two electrodes are connected by a paper
salt bridge saturated with the sample and reference solutions. The overall dimensions of the analyzer
are 2.8 cm x 2.4
cm with a thickness of 150 μm and
require only 10 μL each
of sample and reference solution. Similar analyzers are available for the determination of Na+, Cl–, and CO2.
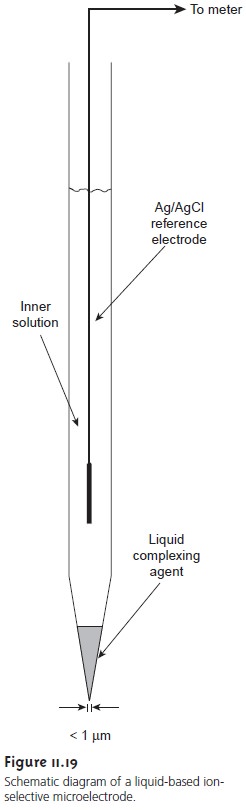
The analysis
of intercellular fluids requires
an ion-selective electrode
that can be inserted directly
into the desired
cell. Liquid-based membrane
microelec- trodes with tip
diameters of less
than 1 μm are constructed by heating and
draw- ing out a hard-glass
capillary tube with an initial diameter of approximately
1–2 mm (Figure
11.19). The tip
of the microelectrode is made hydrophobic by dipping in dichlorodimethyl silane. An inner
solution appropriate for the desired analyte and a Ag/AgCl
wire reference electrode are placed within
the microelec- trode. The tip of the microelectrode is then dipped
into a solution containing the liquid complexing agent. The small
volume of liquid
complexing agent entering the microelectrode is retained within the tip
by capillary action,
eliminating the need
for a solid membrane. Potentiometric microelectrodes have been
developed for a number of clinically important analytes, including
H+, K+, Na+, Ca2+, Cl–, and I–.
Environmental Applications
Although ion-selective electrodes find
use in envi- ronmental analysis, their
application is not as widespread as in clinical analysis. Standard methods
have been developed for the analysis
of CN–, F–, NH3, and NO3– in
water and wastewater. Except for F–, however, other analytical methods
are con- sidered superior. By incorporating the ion-selective electrode into a flow cell, the continuous monitoring of wastewater streams and other flow systems
is possible. Such applications are limited, however,
by the electrode’s response to the analyte’s activity, rather than its concentration. Considerable interest has been shown in the
development of biosensors for the field screening
and monitoring of environmental
samples for a number of priority pollutants.
|
3 |
Potentiometric Titrations
Related Topics