Chapter: Modern Analytical Chemistry: Electrochemical Methods of Analysis
Membrane Potentials - Potentiometric Methods of Analysis
Membrane Potentials
Ion-selective electrodes, such as the glass pH electrode,
function by using a membrane that reacts selectively with a single
ion. Figure 11.10 shows a generic diagram
for a potentiometric electrochemical cell equipped with an
ion-selective electrode. The shorthand notation
for this cell is
Ref(samp) || [A]samp | [A]int || Ref(int)
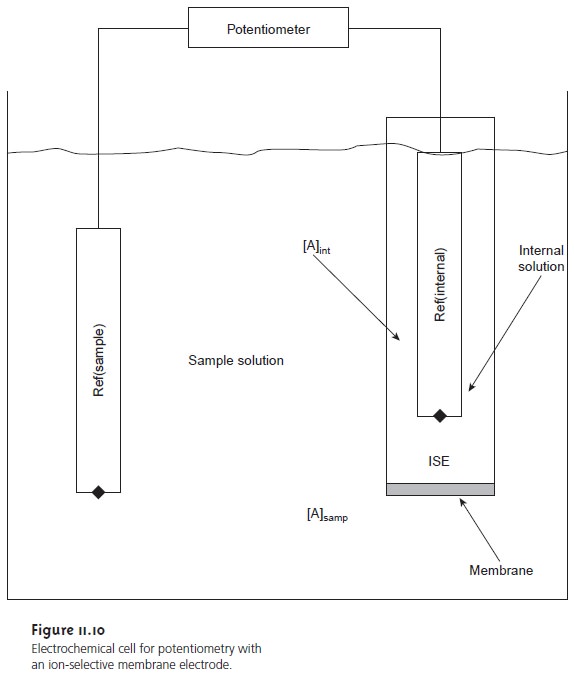
where the membrane is represented by the vertical slash (|) separating the two solu- tions containing analyte. Two reference electrodes are used; one positioned within the internal solution, and
one in the
sample solution. The
cell potential, therefore, is
Ecell = ERef(int) – ERef(samp) + Emem + Elj ……….11.6
where Emem is the potential across the membrane. Since the liquid
junction poten- tial and reference electrode potentials are constant, any change in the cell’s
potential is attributed to the membrane
potential.
Interaction of the analyte with the membrane
results in a membrane potential if there is a difference in the analyte’s concentration on opposite sides of the
mem- brane. One side of the membrane is in contact
with an internal
solution containing a fixed
concentration of analyte,
while the other
side of the membrane is in contact with the sample. Current
is carried through
the membrane by the movement
of ei- ther the
analyte or an ion already
present in the
membrane’s matrix. The
membrane potential is given
by a Nernst-like equation
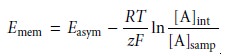 11.7
11.7
where
[A]samp and [A]int are the concentrations of analyte
in the sample and the internal solution, respectively, and z is the analyte’s
charge. Ideally, Emem should be zero when the concentrations of analyte
on both sides of the membrane
are equal. The term Easym, which is called an asymmetry potential, accounts for the fact that the
membrane potential is usually
not zero under these conditions.
Substituting equation 11.7 into equation
11.6, assuming a temperature of 25 °C and rearranging gives
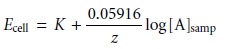 11.8
11.8
where K is a constant accounting for the potentials of the reference electrodes, any
liquid junction potentials, the asymmetry potential, and the concentration of ana- lyte in the internal
solution. Equation 11.8 is a general equation,
and applies to all
types of ion-selective electrodes.
Related Topics