Characterization Applications - Voltammetric Methods of Analysis

Characterization Applications

In the previous section we saw how voltammetry can be used to determine the con- centration of an analyte. Voltammetry also can be used to obtain additional infor- mation, including verifying electrochemical reversibility, determining the number of electrons transferred in a redox reaction, and determining equilibrium constants for coupled chemical reactions. Our discussion of these applications is limited to the use of voltammetric techniques that give limiting currents, although other voltammetric techniques also can be used to obtain the same information.

Electrochemical Reversibility and Determination of n 

In deriving a relationship between E_1/2 and the standard-state potential for a redox couple (11.41), we noted that the redox reaction must be reversible. How can we tell if a redox reaction is re- versible from its voltammogram? For a reversible reaction, equation 11.40 describes the voltammogram.

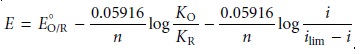
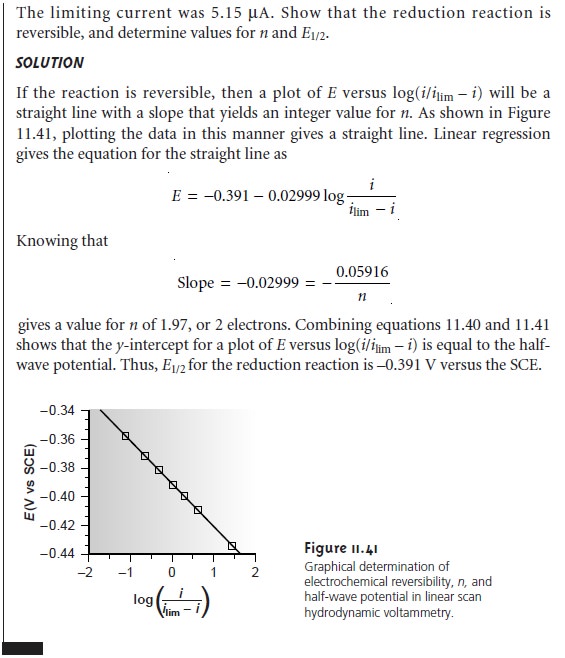
A plot of E versus log(i/i_lim – i) for a reversible reaction, therefore, should be a straight line with a slope of –0.05916/n. In addition, the slope should yield an inte- ger value for n.

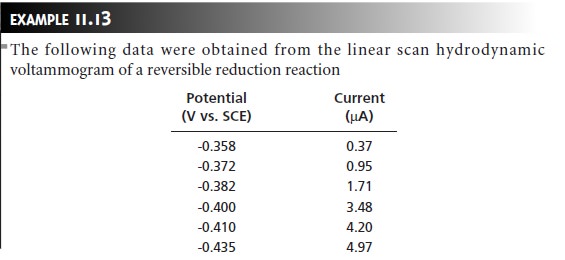
Determining Equilibrium Constants for Coupled Chemical Reactions 

An- other important application of voltammetry is the determination of equilib- rium constants for solution reactions that are coupled to a redox reaction oc- curring at the electrode. The presence of the solution reaction affects the ease of electron transfer, shifting the potential to more negative or more positive potentials. Consider, for example, the reduction of O to R

O+ ne– < = = = = > R

the voltammogram for which is shown in Figure 11.42. If a ligand, L, capable of forming a strong complex with O, is present, then the reaction

O + pL < = = = = > OL_p

also must be considered. The overall reaction, therefore, is

OL_p + ne– < = = = = > R+ pL

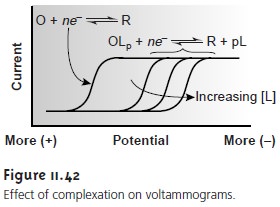
Because of its stability, reduction of the OL_p complex is less favorable than the re- duction of O. As shown in Figure 11.42, the voltammograms for OL_p occur at po- tentials more negative than those for O. Furthermore, the shift in the voltammo- gram depends on the ligand’s concentration.

The shift in the voltammogram for a metal ion in the presence of a ligand may be used to determine both the metal–ligand complex’s stoichiometry and its forma- tion constant. To derive a relationship between the relevant variables we begin with two equations: the Nernst equation for the reduction of O

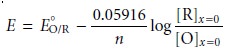
and the stability constant for the complex at the electrode surface

                                   11.42

In the absence of ligand the half-wave potential occurs when [R]_x=0 and [O]_x=0 are equal; thus, from the Nernst equation we have

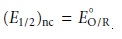                        11.43

where the subscript “nc” signifies that no complex is present.

When ligand is present we must account for its effect on the concentration of O. Solving equation 11.42 for [O]_x=0 and substituting into the Nernst equation gives

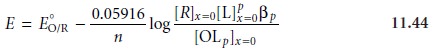
If the ligand is present in excess and the formation constant is sufficiently large, such that all of O is present as the complex, then [R]_x=0 and [OL_p]_x=0 are equal at the half-wave potential, and equation 11.44 simplifies to

where the subscript “c” indicates that the complex is present. Defining ∆E_1/2 as

∆E_1/2 = (E_1/2)_c – (E_1/2)_nc   ……….. 11.46

and substituting equations 11.44 and 11.45 gives, after rearranging

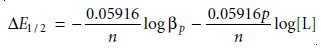
A plot of ∆E_1/2 versus log [L], therefore, gives a straight line. The slope of the line is used to determine the stoichiometric coefficient, p, and the y-intercept gives the value for the formation constant β_p