Potentiometric Measurements - Potentiometric Methods of Analysis

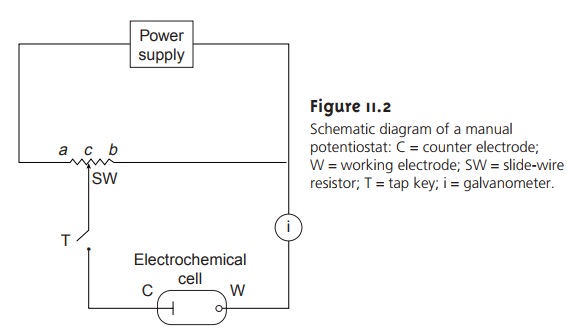
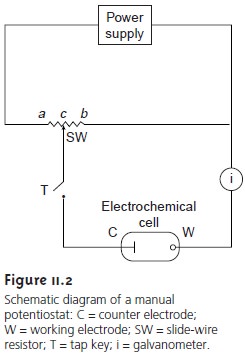
Potentiometric Measurements

Potentiometric measurements are made using a potentiometer to determine the dif- ference in potential between a working or, indicator, electrode and a counter elec- trode (see Figure 11.2). Since no significant current flows in potentiometry, the role of the counter electrode is reduced to that of supplying a reference potential; thus, the counter electrode is usually called the reference electrode. In this section we in- troduce the conventions used in describing potentiometric electrochemical cells and the relationship between the measured potential and concentration.

Potentiometric Electrochemical Cells 

A schematic diagram of a typical potentio- metric electrochemical cell is shown in Figure 11.5. Note that the electrochemical cell is divided into two half-cells, each containing an electrode immersed in a solu- tion containing ions whose concentrations determine the electrode’s potential. This separation of electrodes is necessary to prevent the redox reaction from occurring spontaneously on the surface of one of the electrodes, short-circuiting the electro- chemical cell and making the measurement of cell potential impossible. A salt bridge containing an inert electrolyte, such as KCl, connects the two half-cells. The ends of the salt bridge are fixed with porous frits, allowing ions to move freely be- tween the half-cells and the salt bridge, while preventing the contents of the salt bridge from draining into the half-cells. This movement of ions in the salt bridge completes the electric circuit.

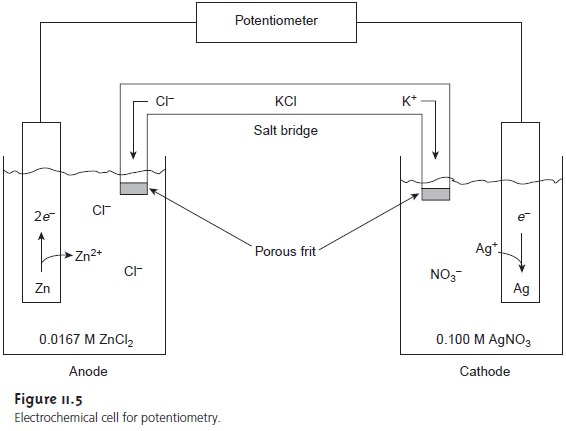
By convention, the electrode on the left is considered to be the anode, where oxidation occurs

Zn(s) < = = = = > Zn2+(aq)+ 2e–

and the electrode on the right is the cathode, where reduction occurs

Ag+(aq)+ e– < = = = = > Ag(s)

The electrochemical cell’s potential, therefore, is for the reaction

Zn(s) + 2Ag+(aq) < = = = = > 2Ag(s)+ Zn2+(aq)

Also, by convention, potentiometric electrochemical cells are defined such that the indicator electrode is the cathode (right half-cell) and the reference electrode is the anode (left half-cell).

Shorthand Notation for Electrochemical Cells 

Although Figure 11.5 provides a useful picture of an electrochemical cell, it does not provide a convenient repre- sentation. A more useful representation is a shorthand, or schematic, notation that uses symbols to indicate the different phases present in the electrochemical cell, as well as the composition of each phase. A vertical slash (|) indicates a phase boundary where a potential develops, and a comma (,) separates species in the same phase, or two phases where no potential develops. Shorthand cell nota- tions begin with the anode and continue to the cathode. The electrochemical cell in Figure 11.5, for example, is described in shorthand notation as

Zn(s) | ZnCl₂ (aq, 0.0167 M) || AgNO₃ (aq, 0.100 M) | Ag(s)

The double vertical slash (||) indicates the salt bridge, the contents of which are nor- mally not indicated. Note that the double vertical slash implies that there is a poten- tial difference between the salt bridge and each half-cell.

Potential and Concentration—The Nernst Equation 

The potential of a potentio- metric electrochemical cell is given as

E_cell = E_c – E_a              ……………………….11.1

where E_c and E_a are reduction potentials for the reactions occurring at the cathode and anode. These reduction potentials are a function of the concentrations of those species responsible for the electrode potentials, as given by the Nernst equation

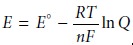
where E° is the standard-state reduction potential, R is the gas constant, T is the temperature in Kelvins, n is the number of electrons involved in the reduction reaction, F is Faraday’s constant, and Q is the reaction quotient.* Under typical laboratory conditions (temperature of 25 °C or 298 K) the Nernst equation becomes

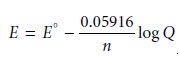                      11.2

where E is given in volts.

Using equation 11.2 the potential of the anode and cathode in Figure 11.5 are

Note, again, that the Nernst equations for both E_c and E_a are written for reduction reactions. The cell potential, therefore, is

Substituting known values for the standard-state reduction potentials (see Appen- dix 3D) and the concentrations of Ag+ and Zn2+, gives a potential for the electro- chemical cell in Figure 11.5 of

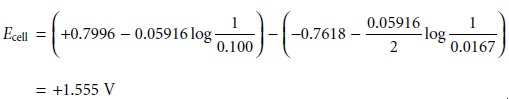
In potentiometry, the concentration of analyte in the cathodic half-cell is gen- erally unknown, and the measured cell potential is used to determine its concentra- tion. Thus, if the potential for the cell in Figure 11.5 is measured at +1.50 V, and the concentration of Zn2+ remains at 0.0167 M, then the concentration of Ag+ is deter- mined by making appropriate substitutions to equation 11.3

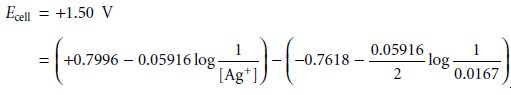
Solving for [Ag+] gives its concentration as 0.0118 M.

Despite the apparent ease of determining an analyte’s concentration using the Nernst equation, several problems make this approach impractical. One problem is that standard-state potentials are temperature-dependent, and most values listed in reference tables are for a temperature of 25 °C. This difficulty can be overcome by maintaining the electrochemical cell at a temperature of 25 °C or by measuring the standard-state potential at the desired temperature.

Another problem is that the Nernst equation is a function of activities, not con- centrations.* As a result, cell potentials may show significant matrix effects. This problem is compounded when the analyte participates in additional equilibria. For example, the standard-state potential for the Fe3+/Fe2+ redox couple is +0.767 V in 1 M HClO₄, +0.70 V in 1 M HCl, and +0.53 in 10 M HCl. The shift toward more negative potentials with an increasing concentration of HCl is due to chloride’s ability to form stronger complexes with Fe3+ than with Fe2+. This problem can be minimized by replacing the standard-state potential with a matrix-dependent for- mal potential. Most tables of standard-state potentials also include a list of selected formal potentials (see Appendix 3D).

A more serious problem is the presence of additional potentials in the electro- chemical cell, not accounted for by equation 11.1. In writing the shorthand nota- tion for the electrochemical cell in Figure 11.5, for example, we use a double slash (||) for the salt bridge, indicating that a potential difference exists at the interface between each end of the salt bridge and the solution in which it is immersed. The origin of this potential, which is called a liquid junction potential, and its signifi- cance are discussed in the following section.

Liquid Junction Potentials 

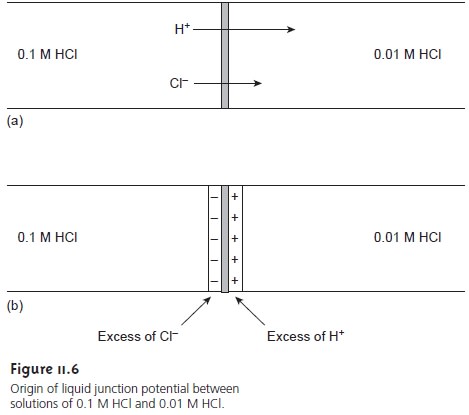
A liquid junction potential develops at the interface between any two ionic solutions that differ in composition and for which the mo- bility of the ions differs. Consider, for example, solutions of 0.1 M HCl and 0.01 M HCl separated by a porous membrane (Figure 11.6a). Since the concentration of HCl on the left side of the membrane is greater than that on the right side of the membrane, there is a net diffusion of H+ and Cl– in the direction of the arrows. The mobility of H+, however, is greater than that for Cl–, as shown by the difference in the lengths of their respective arrows. As a result, the solution on the right side of the membrane develops an excess of H+ and has a positive charge (Figure 11.6b). Simul- taneously, the solution on the left side of the membrane develops a negative charge due to the greater concentration of Cl–. The difference in potential across the mem- brane is called a liquid junction potential, E_lj.

The magnitude of the liquid junction potential is determined by the ionic com- position of the solutions on the two sides of the interface and may be as large as 30–40 mV. For example, a liquid junction potential of 33.09 mV has been measured at the interface between solutions of 0.1 M HCl and 0.1 M NaCl.2 The magnitude of a salt bridge’s liquid junction potential is minimized by using a salt, such as KCl, for which the mobilities of the cation and anion are approximately equal. The magni- tude of the liquid junction potential also is minimized by incorporating a high con- centration of the salt in the salt bridge. For this reason salt bridges are frequently constructed using solutions that are saturated with KCl. Nevertheless, a small liquid junction potential, generally of unknown magnitude, is always present.

When the potential of an electrochemical cell is measured, the contribution of the liquid junction potential must be included. Thus, equation 11.1 is rewritten as

Ecell = Ec – Ea + Elj

Since the junction potential is usually of unknown value, it is normally impossible to directly calculate the analyte’s concentration using the Nernst equation. Quanti- tative analytical work is possible.