Physics - Laws of Motion: Important Questions | 11th Physics : UNIT 3 : Laws of Motion
Chapter: 11th Physics : UNIT 3 : Laws of Motion
Laws of Motion: Important Questions
Laws of Motion - Physics
Short Answer
Questions
1.
Explain the concept of inertia. Write two examples each for inertia of motion,
inertia of rest and inertia of direction.
2.
State Newton’s second law.
3.
Define one newton.
4.
Show that impulse is the change of momentum.
5.
Using free body diagram, show that it is easy to pull an object than to push
it.
6.
Explain various types of friction. Suggest a few methods to reduce friction.
7.
What is the meaning by ‘pseudo force’?
8.
State the empirical laws of static and kinetic friction.
9.
State Newton’s third law.
10.
What are inertial frames?
11.
Under what condition will a car skid on a leveled circular road?
Long Answer
Questions
1.
Prove the law of conservation of linear momentum. Use it to find the recoil
velocity of a gun when a bullet is fired from it.
2.
What are concurrent forces? State Lami’s theorem.
3.
Explain the motion of blocks connected by a string in i) Vertical motion ii)
Horizontal motion.
4.
Briefly explain the origin of friction. Show that in an inclined plane, angle
of friction is equal to angle of repose.
5.
State Newton’s three laws and discuss their significance.
6.
Explain the similarities and differences of centripetal and centrifugal forces.
7.
Briefly explain ‘centrifugal force’ with suitable examples.
8.
Briefly explain ‘rolling friction’.
9.
Describe the method of measuring angle of repose.
10.
Explain the need for banking of tracks.
11.
Calculate the centripetal acceleration of Moon towards the Earth.
Numerical Problems
1. A force of 50N act on the object of mass 20 kg. shown in the figure. Calculate the acceleration of the object in x and y directions.
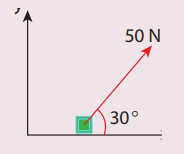
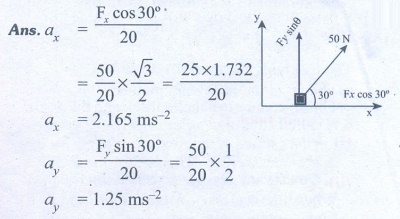
Ans: ax=2.165 ms-2; ay=1.25 ms-2
2. A spider of mass 50 g is hanging on a string of a cob web as shown in the figure. What is the tension in the string?

Answer:
T = mg
Mass (m) = 50g = 0.050 kg
g = 9.8 ms-2
T = 0.050 × 9.8
= 0.49 N.
Ans: T=0.49N
3. What is the reading shown in spring balance?
Answer:
Zero, 9.8 N. The weight of the body is equal to the acceleration due to gravity.
Ans: Zero, 9.8 N
4. The physics books are stacked on each other in the sequence: +1 volumes 1 and 2; +2 volumes 1 and 2 on a table.
a. Identify the forces acting on each book and draw the free body diagram.
b. Identify the forces exerted by each book on the other.
Answer:
(i) Gravitation force mg acting downwards on the books +1 vol. 1, vol. 2, +2. vol. 1, +2 vol. 2.
(ii) Upward normal force (NB) exerted by book B(NB).
(iii) Normal contact force (N) exerted by the vol. 2 on the book vol. 1 and so on.
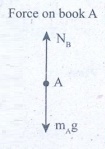
Forces on book A:
(i) Downward gravitational force exerted by the Earth (mAg)
(ii) Upward normal force (NB) exerted by book B (NB)
The free body diagram for book A is as shown in the following picture.
Force on book B
(i) Downward gravitational force exerted by Earth (mBg)
(ii) Downward force exerted by book A (NA)
(iii)Upward normal force exerted by book C (Nc)

Forces oil book C:
(i) Downward gravitational force exerted by Earth (mcg)
(ii) Downward force exerted by book B(NB)
(iii) Upward normal force exerted by the book (ND)
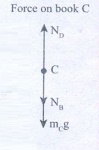
Forces on book D:
(i) Downward gravitational force exerted by Earth (mDg)
(ii) Downward force exerted by book C (Nc)
(iii) Upward force exerted by the table (Ntable)

5. A bob attached to the string oscillates back and forth. Resolve the forces acting on the bob in to components. What is the acceleration experience by the bob at an angle θ.
Answer:
(i) The radial force = T - mg cos θ provides centripetal force but no torque about support O.
(ii) The tangential force mg sin θ provide the restoring torque.
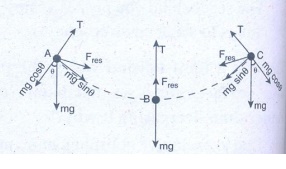
Tangential acceleration α = tangential force/ m
= g sin θ
Centripetal acceleration = T – mg cos θ / m
Ans: Tangential acceleration = g sinθ ; centripetal acceleration = (T−mg cosθ)/m
6. Two masses m1 and m2 are connected with a string passing over a frictionless pulley fixed at the corner of the table as shown in the figure. The coefficient of static friction of mass m1 with the table is μs. Calculate the minimum mass m3 that may be placed on m1to prevent it from sliding. Check if m1=15 kg, m2=10 kg, m3=25 and μs =0.2
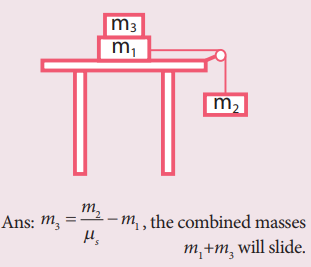
Answer:

7. Calculate the acceleration of the bicycle of mass 25 kg as shown in Figures 1 and 2.
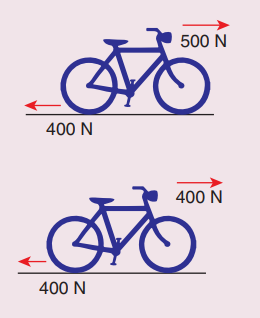
Answer
(i) Net force F1 = 500 - 400 = 100 N
Mass m = 25 kg; a = ?
Acceleration a = F/ m
a = 100/ 25 = 4 ms-2
(ii) Net force acting on cycle F2 = 400 - 400 = 0.
a = 0.
Ans: a=4 ms-2, zero
8. Apply Lami’s theorem on sling shot and calculate the tension in each string ?
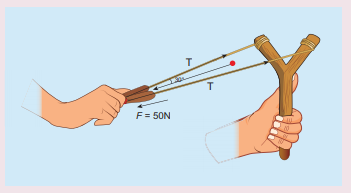
Answer:
Force F = mg = 50 N;
θ = 30 °
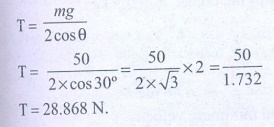
T= 28.868 N.
Ans: T= 28.868N.
9. A football player kicks a 0.8 kg ball and imparts it a velocity 12 ms-1. The contact between the foot and ball is only for one- sixtieth of a second. Find the average kicking force.
Answer:
Time of contact = 1/60 s
Mass of ball = 0.8 kg.
Velocity v = 12 ms-1
Average force = Δp/Δt
Favg = 0.8x12 / (1/60)
= 0.8 × 12 × 60 = 576 N .
Average kicking force = 576 N.
Ans: 576N.
10. A stone of mass 2 kg is attached to a string of length 1 meter. The string can withstand maximum tension 200 N. What is the maximum speed that stone can have during the whirling motion?
Answer:
Length, r = 1 m
Mass = 2 kg

Ans: vmax=10ms-1
11. Imagine that the gravitational force between Earth and Moon is provided by an invisible between the Moon and Earth. What is the tension that exists in this invisible string due to Earth’s centripetal force?
(Mass of the Moon = 7.34 × 1022 kg, Distance between Moon and Earth = 3.84 × 108 m)
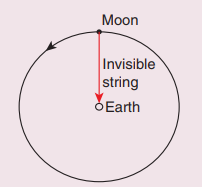
Answer
Tension T = Centripetal force
Centripetal force F = m × Centripetal acceleration
F = m × 0.00272
= 7.34 × 1022 × 0.00272 = 0.0199 × 1022
= 1.99 × 1020 = 2 × 1020N.
(i) The centripetal acceleration is given by a = v2/r. This expression explicitly depends on Moon’s speed which is non-trivial. We can work with the formula
ω2Rm = am
(ii) am is centripetal acceleration of the Moon due to Earth’s gravity,
ω is angular velocity.
(iii) Rm is the distance between Earth and the Moon, which is 60 times the radius of the Earth
Rm = 60R = 60 × 6.4 × 106 = 384 × 106 m.
(iv) As we know the angular velocity ω = 2π/T and T = 27.3 days = 27.3 × 24 × 60 × 60 second = 2.358 × 106 sec. By substituting these values in the formula for acceleration
am = (4π2)(384×106) / (2.358×106)2 = 0.00272 ms-2.
The centripetal acceleration of Moon towards the Earth is 0.00272 ms-2.
T ~ 2 × 1020N
Ans: T = 2 x 1020 N.
12. Two bodies of masses 15 kg and 10 kg are connected with light string kept on a smooth surface. A horizontal force F=500 N is applied to a 15 kg as shown in the figure. Calculate the tension acting in the string
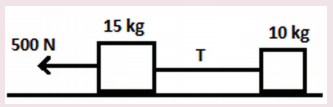
Answer:

Ans: T = 200N .
13. People often say “For every action there is an equivalent opposite reaction”. Here they meant ‘action of a human’. Is it correct to apply Newton’s third law to human actions? What is mean by ‘action’ in Newton third law? Give your arguments based on Newton’s laws.
Answer:
Newton’s third law is applicable to only human’s actions which involves physical force. Third law is not applicable to human’s psychological! actions or thoughts.
Ans: Newton’s third law is applicable to only human’s actions which involves physical force. Third law is not applicable to human’s psychological actions or thoughts
14. A car takes a turn with velocity 50 m s-1 on the circular road of radius of curvature 10 m. calculate the centrifugal force experienced by a person of mass 60kg inside the car?
Answer:
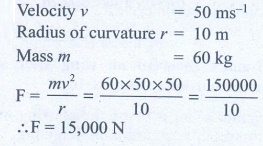
Ans: 15,000 N
15. A long stick rests on the surface. A person standing 10 m away from the stick. With what minimum speed an object of mass 0.5 kg should he thrown so that it hits the stick. (Assume the coefficient of kinetic friction is 0.7).
Ans: 11.71 m s-1

Conceptual Questions
1. Why it is not possible to push a car from inside?
Answer:
(i) When you push a car from inside, the reaction force of your pushing is balanced out by your body moving backward.
(ii) The seat behind you pushes against to bring things to static equilibrium.
2. There is a limit beyond which the polishing of a surface increases frictional resistance rather than decreasing it why?
Answer:
(i) Due to excessive polishing, more molecules of the two surfaces come closer. Thus they form more bonds and offer great resistances.
(ii) Because friction arises due to molecular adhesion i.e. due to electrostatic forces.
3. Can a single isolated force exist in nature? Explain your answer.
Answer:
No, a single isolated force cannot exist in nature because it violates the Newton's third law.
4. Why does a parachute descend slowly?
Answer:
A parachute is a device used to slow down on object that is falling towards the ground. When the parachute opens, the air resistance increases. So the person can land safely.
5. When walking on ice one should take short steps. Why?
Answer:
It is to avoid slipping. Smaller step causes more normal force and thereby more friction.
6. When a person walks on a surface, the frictional force exerted by the surface on the person is opposite to the direction of motion. True or false?
Answer:
False. The frictional force exerted by the surface is not opposite to the direction of motion.
7. Can the coefficient of friction be more than one?
Answer:
Yes, μ > 1, friction is stronger than normal force.
8. Can we predict the direction of motion of a body from the direction of force on it?
Answer
In free body diagrams, the force of friction is always parallel to the surface of contact. The force of kinetic friction is always opposite the direction of motion.
9. The momentum of a system of particles is always conserved. True or false?
Answer:
True. The momentum of a system of particles is always conserved.
Related Topics