Application of Newton’s Laws: Particle Moving in an Inclined Plane

Particle Moving in an Inclined Plane

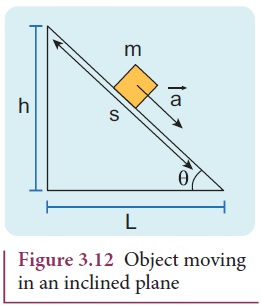
When an object of mass m slides on a frictionless surface inclined at an angle Î¸ as shown in the Figure 3.12, the forces acting on it decides the

a.        acceleration of the object

b.        speed of the object when it reaches the bottom

The force acting on the object is

(i)  Downward gravitational force (mg)

(ii)  Normal force perpendicular to inclined surface (N)

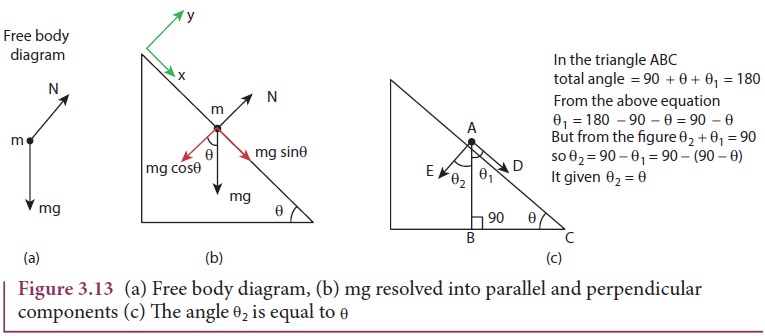
To draw the free body diagram, the block is assumed to be a point mass (Figure 3.13 (a)). Since the motion is on the inclined surface, we have to choose the coordinate system parallel to the inclined surface as shown in Figure 3.13 (b).

The gravitational force mg is resolved in to parallel component mg sinθ along the inclined plane and perpendicular component mg cosθ perpendicular to the inclined surface (Figure 3.13 (b)).

Note that the angle made by the gravitational force (mg) with the perpendicular to the surface is equal to the angle of inclination Î¸ as shown in Figure 3.13 (c).

There is no motion(acceleration) along the y axis. Applying Newton’s second law in the y direction

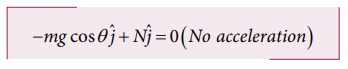
By comparing the components on both sides, N âˆ’ mg cosθ = 0

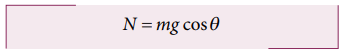
The magnitude of normal force (N) exerted by the surface is equivalent to mg cosθ .

The object slides (with an acceleration) along the x direction. Applying Newton’s second law in the x direction

Note that the acceleration depends on the angle of inclination Î¸ . If the angle Î¸ is 90 degree, the block will move vertically with acceleration a = g.

Newton’s kinematic equation is used to find the speed of the object when it reaches the bottom. The acceleration is constant throughout the motion.

The acceleration a is equal to mg sinθ. The initial speed (u) is equal to zero as it starts from rest. Here s is the length of the inclined surface.

The speed (v) when it reaches the bottom is (using equation (3.3))