Chapter: 11th Physics : UNIT 3 : Laws of Motion
Application of Newton’s Laws: Motion of Connected Bodies
Motion of Connected Bodies
When objects are connected by strings and a force F is applied either vertically or horizontally or along an inclined plane, it produces a tension T in the string, which affects the acceleration to an extent. Let us discuss various cases for the same.
Case 1: Vertical motion
Consider two blocks of masses m1 and m2 (m1> m2) connected by a light and inextensible string that passes over a pulley as shown in Figure 3.15.
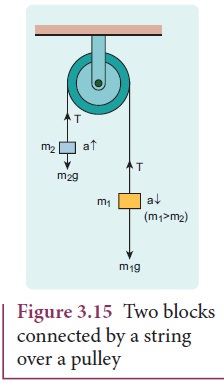
Let the tension in the string be T and acceleration a. When the system is released, both the blocks start moving, m2 vertically upward and m1 downward with same acceleration a. The gravitational force m1g on mass m1 is used in lifting the mass m2.
The upward direction is chosen as y direction. The free body diagrams of both masses are shown in Figure 3.16.
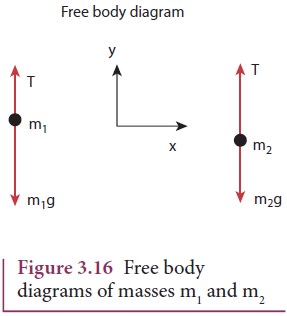
Applying Newton’s second law for mass m2
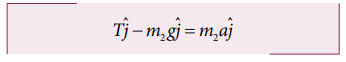
The left hand side of the above equation is the total force that acts on m2 and the right hand side is the product of mass and acceleration of m2 in y direction.
By comparing the components on both sides, we get

By comparing the components on both sides, we get

This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest.
To find the tension acting on the string, substitute the acceleration from the equation (3.12) into the equation (3.9).

By taking m2g common in the RHS of equation (3.13)
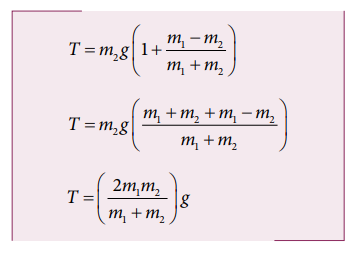
Equation (3.12) gives only magnitude of acceleration.

Case 2: Horizontal motion
In this case, mass m2 is kept on a horizontal table and mass m1 is hanging through a small pulley as shown in Figure 3.17. Assume that there is no friction on the surface.
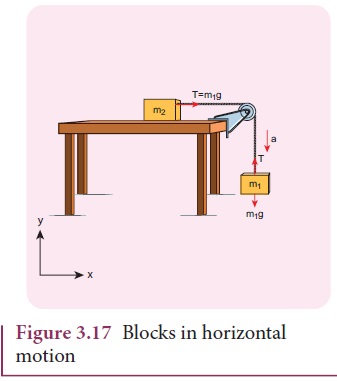
As both the blocks are connected to the unstretchable string, if m1 moves with an acceleration a downward then m2 also moves with the same acceleration a horizontally.
The forces acting on mass m2 are
i. Downward gravitational force (m2g)
ii. Upward normal force (N) exerted by the surface
iii. Horizontal tension (T) exerted by the string
The forces acting on mass m1 are
i. Downward gravitational force (m1g)
ii. Tension (T) acting upwards
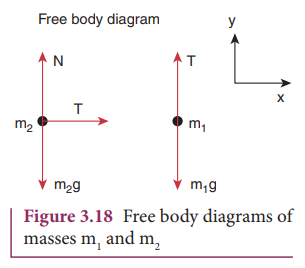
The free body diagrams for both the masses is shown in Figure 3.18.
Applying Newton’s second law for m1
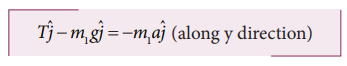
By comparing the components on both sides of above equation,

By comparing the components on both sides of above equation,

Tension in the string can be obtained by substituting equation (3.17) in equation (3.15)
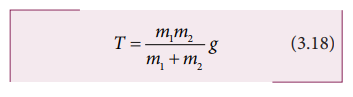
Comparing motion in both cases, it is clear that the tension in the string for horizontal motion is half of the tension for vertical motion for same set of masses and strings.
This result has an important application in industries. The ropes used in conveyor belts (horizontal motion) work for longer duration than those of cranes and lifts (vertical motion).
Related Topics