Long Questions and Answer

Laws of Motion | Physics

Long Answer Questions

1. Prove the law of conservation of linear momentum. Use it to find the recoil velocity of a gun when a bullet is fired from it.

● When two particles interact with each other, they exert equal and opposite forces on each other. The particle 1 exerts force  on particle 2 and particle 2 exerts an exactly equal and opposite force  on particle 1.

● According to Newton's third law.

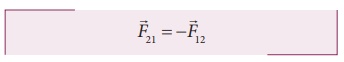               ………..(1)

● In terms of momentum of particles, the force on each particle (Newton's II law) can be written as

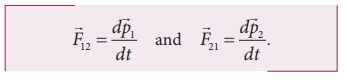         ………(2)

●  Here  is the momentum of particle 1 which change due to Force  exerted by particle 2 and  is the momentum of particle 2.

● This changes due to  exerted by particle

1. Substitute equation 2 in equation 1.

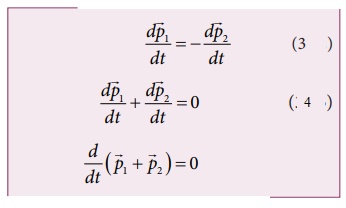
● It implies that + = constant vector +  is the total 

● linear momentum of the two particles ( =+)

● It is also called as total linear momentum of the system.

● "If there are no enternal forces acting on the system, then the total linear momentum of the system (). is always a constant vector".

● The total linear momentum of the system is conserved in time.

Rewil velocity of a gun when bullet is fired from it:

● Let 'M' be the mass of gun and m be, the mass of the bullet.

● Initially both the gun and bullet are at rest on firing the gun,

● Suppose the bullet moves with velocity V and the gun moves with velocity v. According to the principle of conservation of momentum,

● Total momentum of gun and bullet before firing = Total momentum of gun and bullet after firing.

(ie)  (Total momentum before firing is zero because of both are in rest)

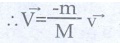
● The negative sign shows that 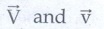 are in opposite direction (ie) as the bullet moves forward, the gun will move in backward direction. The backward motion of the gun is called recoil of the gun and this velocity is recoil velocity.

2. What are concurrent forces? State Lami’s theorem.

Concurrent forces:

● A collection of forces is said to be concurrent, it the line of forces act at a common point.

● Cocurrent forces not be in the same plane. If they are in the same plane, they are concurrent as well as coplanar forces.

Lami's Theorem:

● If the system of three concurrent and coplanar forces are in equilibrium, Lami's theorem states that the magnitude of each force of the system is proportional to sine of the angle between other two forces. The constant of proportionality is same for all three forces.

● Consider three coplanar and concurrent forces,  which act at a common point.

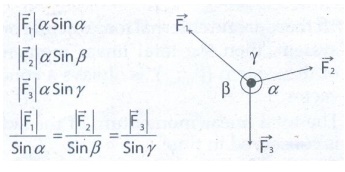
● Lami's theorem is useful to analyse the forces acting on objects which are in static equilibrium

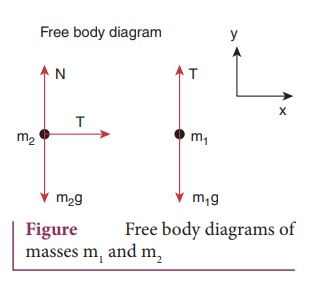
3. Explain the motion of blocks connected by a string in i) Vertical motion ii) Horizontal motion.

i) Vertical motion:

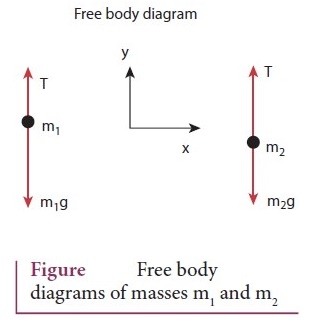
● Consider two blocks of masses m₁ and m₂ (m₁ > m₂) connected by a light and in extensible string that passes over a pulley as shown in figure.

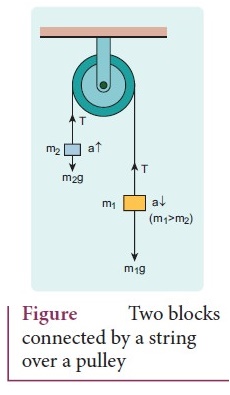
● Let the tension in the string be T and acceleration a.

● When the system is released, both the blocks start moving, m₂ vertically upward and m₂ downward with same acceleration

a. The gravitational force m₁ g on mass m₁ is used in lifting the mass m₂.

● The upward direction is chosen as Y direction

Free body diagram shown in figure

● Applying Newton’s second law for mass m₂,

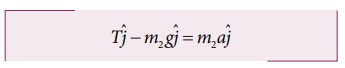
● By comparing the components on both sides

we get, T − m₂g = m₂a    ………….(1)

Similarly for mass m₁ 

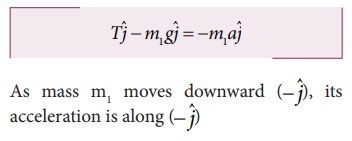
● By comparing the component on both sides we get m₁g - T = m₁a  ………… (2)

● Adding equation (1) and (2)

we get (m₁ - m₂) g = (m₁ + m₂)a         ………. (3)

● From the equation (3), the acceleration of both the masses is

a = (m₁−m₂ / m₁+m₂)g        ……….. (4)

● If both the masses are equal (m₁ − m₂) from equation (4) a = 0

● Tension on the string can be obtained by substituting the acceleration from the eqn. (4) in to eqn (1)

 T = m₂g + m₂(m₁−m₂ / m₁+m₂)g        ……….. (5)

● By taking m₂ g common in the RHS of eqn (5) we get

T = ( 2m₁m₂ / m₁+m₂ )g

● Equation (4) gives only magnitude of acceleration for mass m₁, the acceleration vector is

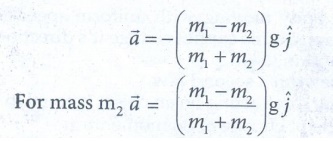
ii) Horizontal motion:

In this case, mass m₂ is kept on a horizontal table and mass m₁ is hanging through a small pulley.

The forces acting on a mass m₂, and m₁ are shown in free body diagram

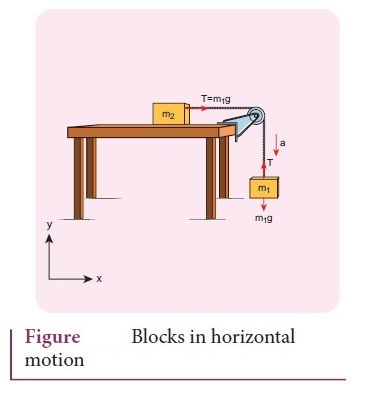
Applying Newton's second law for m₁

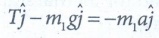 (along y direction)

By comparing the components on both side,

T – m₁g = -m₁a     …………… (6)

Similarly for m₂

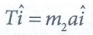(along x direction)

By comparing the components on both side,

T − m₂a    ………… (7)

There is no acceleration along Y direction for m₂

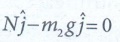
N - m₂g = 0

(ie) N = m₂g    …………… (8)

Substituting equation (7) in eqn. (6), we get

a = ( m₁ / [m₁+m₂] ) g         …………… (9)

Substituting equation (9) in equation (7) we get, Tension in the string

T = ( m₁m₂ / [m₁+m₂] ) g        …………… (10)

Comparing motion in both cases, it is clear that the tension in the string for horizontal motion is half of the tension for vertical motion for same set of masses and strings.

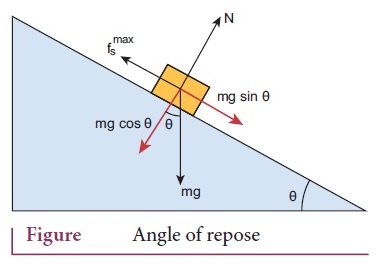
4. Briefly explain the origin of friction. Show that in an inclined plane, angle of friction is equal to angle of repose.

● The force of friction is due to the atomic or molecular forces of attraction between the two surfaces at the points of actual contacts.

● Due to the surface irregularities, the actual area of contact is much smaller than the apparent area of contact.

● The pressure at the point of contact is very large, molecular bonds are formed at these points.

● When one body is pulled over the other, the bonds breaks, the material is deformed and new bond are formed.

● The local determation sends vibration waves into the bodies. These vibrations finally damp out and energy appears as heat. Hence a force is needed to start or maintain the motion.

Angle of friction is equal to angle of repose:

● Consider an inclined plane on which an object is placed.

● Let the angle which this plane make with the horizontal be θ.

● As θ is increased for a particular value of θ the object begins slide down. This value is called angle of repose.

● The component of force perpendicular to the inclined plane (mg cosθ) is balanced by the normal force (N)

(ie.) N = mg cosθ  ………… (1)

● When the object just begins to move, the static friction affairs its maximum value

 ƒ_s = ƒ_s^max = μ_sN = μ_s mgcosθ ……….. (2)

● This friction also satisfies the relation

ƒ_s^max = mg sinθ       ……………. (3)

dividing eqn. (2 and 1) ƒ_s^max

ƒ_s^max / N= sinθ / cosθ = tanθ

μ_s = sinθ / cosθ

μ_s = tanθ        ……………. (4)

● From the definition θ is angle of friction. States that the co efficient of static friction is equal to tangent of the angle of friction.

● Thus the angle of repose is the same as angle of friction.

5. State Newton’s three laws and discuss their significance.

Newton's first law:

Every object continues to be in the state of rest (or) of uniform motion (constant velocity) unless there is external force acting on it.

● A body at rest continues in its state of rest.

● A body in motion continues moving in a straight line with a uniform speed.

● A body moving with uniform speed in a straight line cannot change it's direction of motion itself.

Newton's second law:

● The force acting on an object is equal to the rate of change of its momentum

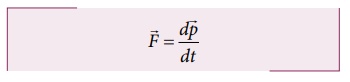
● Whenever the momentum of the body changes there must be a force acting on it.

● The momentum of the object is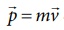 

● In most cases the mass of the object remains constant during the motion.

● This implies that it there is a change in velocity then there must be a force acting on it.

● The force and acceleration are always in same direction.

● This Law only valid for inertial frames.

Newton's third law:

● In this law, action and reaction pair of forces do not act on the same body.

But on two different bodies.

● Any one of the forces can be called as an action force and the other the reaction force.

● An isolated force (or) single force cannot exist is nature.

● Newton's third law is valid in both inertial and non-inertial frames

6. Explain the similarities and differences of centripetal and centrifugal forces.

Centripetal force

1. It is real force which is exerted on the body by the external agencies like gravitational force, tension in the string, normal force etc.

2. Acts in both inertial and non-inertial frames

3. It acts towards the axis of rotation (or) centre of the circle in circular motion.

| F_cp | = mω²r = mv² / r

4. Real force and has real effects

5. Origin of centripetal forces is interaction between two objects.

6. In inertial frames centripetal force has to be included when free body diagrams are drawn.

Centrifugal force

1. It is pseudo force (or) fictitious force which cannot arise from gravitational force, tension force, normal force etc

2. Acts only in rotating frames (non-inertial frame)

3. It acts outwards from the axis of rotation (or) radially outwards from the center of circular motion.

| F_cf | = mω²r = mv² / r

4. Pseudo force but has real effects

5. Origin of centrifugal force is inertia. It does not arise from interaction.

6. In rotating frames, both centripetal and centrifugal force have to be included when free body diagrams are drawn.

7. Briefly explain ‘centrifugal force’ with suitable examples.

● Consider the case of whirling motion of a stone tied to a string.

● Assume that the stone has angular velocity 'ω' in the inertial frame (at rest)

● If the motion of the stone is observed from frame which is also rotating along with the stone with same angular velocity ω, then, the stone appears to be at rest.

● This imples that in addition to the inward centripetal force - mω²r, there must be an equal and opposite force that acts on the stone outward with value + mω²r.

● So the total force acting on the stone in rotating frame is equal to zero (−mω²r + + mω²r = 0). This outward force + mω²r is called centrifugal force.

● The word centrifugal means 'flee from centre'. Note that the centrifugal force appears to act on the particle, only when we analyse the motion from a rotating frame.

● With respect to an inertial frame there is only centripetal force which is given by tension in the string. For this reason centrifugal force is called 'Pseudo force'

● A Pseudo force has no origin. It arises due to non-inertial nature of frame considered.

8. Briefly explain ‘rolling friction’.

● The force of friction that comes into play when a body rolls over the surface of another body is called rolling friction.

● When a wheel rolls over a road, rolling friction comes into play.

● In rolling motion when a wheel moves on a surface, the point of contact with surface is always at rest. Since the point of contact is at rest, there is no relative motion between the wheel and surface. Hence the frictional force is very less.

● If an object moves with out wheel, there is a relative motion between the object and the surface. As a result frictional force is large. This makes it difficult to move the object.

● Ideally in pure rolling, motion of the point of contact with the surface should be at rest, but in practice it is not so.

● Due to elastic nature of the surface at the point of contact there will be some deformation on the object at this point on the wheel or surface.

● Due to this deformation, there will be minimal friction between wheel and surface. It is called rolling friction.

● In fact 'rolling friction' is much smaller than kinetic friction.

9. Describe the method of measuring angle of repose.

Consider an inclined plane on which an object is place. Let the angle which this plane makes with the horizontal be θ.

● For small angle of θ the object may not slide down. As θ is increased, for particular value of θ, the object begins to slide down. This value is called angle of repose.

● Hence, the angle of repose is the angle of inclined plane with the horizontal such that on object placed on it begins to slide.

● Let us consider the various forces. The gravitational force mg is resolved into component parallel (mg Sinθ) and perpendicular (mg cosθ) to the inclined Plane.

● The component of force parallel to the inclined plane (mg sinθ) tries to move the object down.

● The component of force perpendicular to the inclined plane (mg cosθ) is balanced by the normal force (N)

N = mg cosθ          ……………….. (1)

● When the object just begins to move, the static friction attains its maximum value.

ƒ_s^max = μ_sN = μ_s mg cosθ       …………(2)

This friction also satisfies the relation

ƒ_s^max = mg sinθ           ………………(3)

Dividing equations (2) by 1, we get. ƒ_s^max / N = sinθ / cosθ

● From the definition of angle of friction, we also know that, tanθ = μ_s in which θ is the angle of friction. Thus the angle of repose is the same as angle of friction.

10. Explain the need for banking of tracks.

● In a leveled circular road, skidding mainly depends on the co efficient of static friction μ_s

● To avoid this problem usually the outer edge of the road is slightly raised compared to inner edge. This is called banking of road (or) tracks. This introduces an inclination and the angle is called banking angle.

● Let the surface of the road make angle θ with horizontal surface. Then the normal force makes the same angle θ with the vertical.

● When the car takes a turn, there are two forces acting on the car.

1. Gravitational force mg (downwards)

2. Normal force N (perpendicular to surface)

● We can resolve the normal force into two components. Ncosθ and Nsinθ.

● The component Ncos0 balances the downward gravitational force, 'mg' and component Nsinθ will provide the necessary centripetal acceleration.

● By using Newton's Second law.

N cos θ = mg             ………..(1)

N sin θ = mv² / r     ……….. (2)

dividing equation (2) and (1), We get

tan θ = v² / rg

∴ v = √[rg tanθ]

Thus,

● The banking angle θ and radius of curvature of the road (or) track determines the safe speed of car at the turning.

● If the speed of car exceed this safe speed, then it starts to skid out ward but frictional force comes into effect and provides an additional centripetal force to prevent the outward skidding.

● At the same time, if the speed of the car is little lesser than safe speed, it starts to skid inward and frictional force comes into effect, which reduces centripetal force to prevent inward skidding.

● However if the speed of the vehicle is sufficiently greater than the correct speed, then frictional force cannot stop the car from skidding.

11. Calculate the centripetal acceleration of Moon towards the Earth.

● The centripetal acceleration is given by a = v² / r . This expression explicitly depends on moon's speed which is Non trivial.

ω² R_m = a_m

a_m is centripetal acceleration of the moon due to Earth's gravity. ω is angular velocity.

R_m is the distance between earth and the moon, which is 60 times the radius of the earth.

R_m = 60R = 60×6.4×10⁶ = 384×10⁶m

The angular velocity ω = 2π / T

Here T = 27.3 days = 27.3 × 24 × 60 × 60 sec

= 2.358 × 10⁶ sec

By substituting these values in the formula for acceleration. a_m = ω² R_m

 = ω² R_m

 = (2π / T)² R_m

 = [4π² / T² ] R_m

 a_m = [ (4 π²) (384 × 10⁶) ] / [ (2.358 × 10⁶)² ]

 = 0.00272 ms^-2

The centripetal acceleration of moon towards the earth 0.00272 ms^-2