Chapter: 11th Physics : UNIT 3 : Laws of Motion
Dynamics of Circular Motion
DYNAMICS OF CIRCULAR
MOTION
In
the previous sections we have studied how to analyse linear motion using
Newton’s laws. It is also important to know how to apply Newton’s laws to
circular motion, since circular motion is one of the very common types of
motion that we come across in our daily life. A particle can be in linear
motion with or without any external force. But when circular motion occurs
there must necessarily be some force acting on the object. There is no Newton’s
first law for circular motion. In other words without a force, circular motion
cannot occur in nature. A force can change the velocity of a particle in three
different ways.
1.
The magnitude of the velocity can be changed without changing the direction of
the velocity. In this case the particle will move in the same direction but
with acceleration.
Examples
1.
Particle falling down vertically, bike moving in a straight road with
acceleration.
2.
The direction of motion alone can be changed without changing the magnitude
(speed). If this happens continuously then we call it ‘uniform circular
motion’.
3.
Both the direction and magnitude (speed) of velocity can be changed. If this
happens non circular motion occurs. For example oscillation of a swing or
simple pendulum, elliptical motion of planets around the Sun.
In
this section we will deal with uniform circular motion and non-circular motion.
Centripetal force
If
a particle is in uniform circular motion, there must be centripetal
acceleration towards the center of the circle. If there is acceleration then
there must be some force acting on it with respect to an inertial frame. This
force is called centripetal force.
As
we have seen in chapter 2, the centripetal acceleration of a particle in the
circular motion is given by a = v2/r and
it acts r towards center of the
circle. According to Newton’s second law, the centripetal force is given by
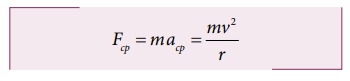
The
word Centripetal force means center seeking force.
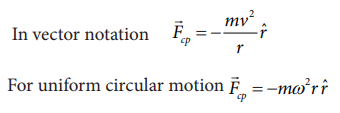
The
direction -rˆ points towards the center of the circle which is the direction of
centripetal force as shown in Figure 3.38.

It
should be noted that ‘centripetal force’ is not other forces like gravitational
force or spring force. It can be said as ‘force towards center’. The origin of
the centripetal force can be gravitational force, tension in the string,
frictional force, Coulomb force etc. Any of these forces can act as a
centripetal force.
1.
In the case of whirling motion of a stone tied to a string, the centripetal
force on the particle is provided by the tensional force on the string. In
circular motion in an amusement park, the centripetal force is provided by the
tension in the iron ropes.
2.
In motion of satellites around the Earth, the centripetal force is given by
Earth’s gravitational force on the satellites. Newton’s second law for
satellite motion is

Where
r- distance of the planet from the
center of the Earth.

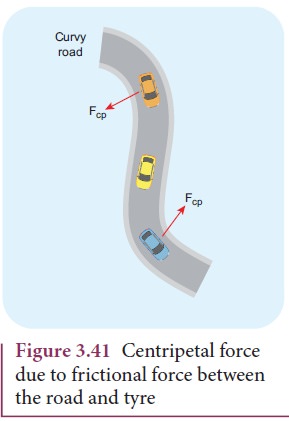
3.
When a car is moving on a circular track the centripetal force is given by the
frictional force between the road and the tyres.
Newton’s
second law for this case is

Even
when the car moves on a curved track, the car experiences the centripetal force
which is provided by frictional force between the surface and the tyre of the
car. This is shown in the Figure 3.41.
4. When the planets orbit around the Sun, they experience centripetal force
towards the center of the Sun. Here gravitational force of the Sun acts as
centripetal force on the planets as shown in Figure 3.42.
Newton’s
second law for this motion
Gravitational
force of Sun on the planet = mv2/r
Vehicle on a leveled circular road
When
a vehicle travels in a curved path, there must be a centripetal force acting on
it. This centripetal force is provided by the frictional force between tyre and
surface of the road. Consider a vehicle of mass ‘m’ moving at a speed ‘v’ in
the circular track of radius ‘r’. There are three forces acting on the vehicle
when it moves as shown in the Figure 3.43
1.
Gravitational
force (mg) acting downwards
2.
Normal
force (mg) acting upwards
3.
Frictional
force (Fs) acting horizontally inwards along the road

Suppose
the road is horizontal then the normal force and gravitational force are
exactly equal and opposite. The centripetal force is provided by the force of
static friction Fs between the tyre and surface of the road which
acts towards the center of the circular track,
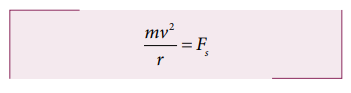
As
we have already seen in the previous section, the static friction can increase
from zero to a maximum value

The
static friction would be able to provide necessary centripetal force to bend
the car on the road. So the coefficient of static friction between the tyre and
the surface of the road determines what maximum speed the car can have for safe
turn.
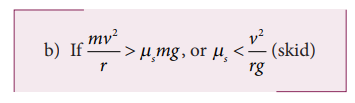
If
the static friction is not able to provide enough centripetal force to turn,
the vehicle will start to skid.
Banking of Tracks
In
a leveled circular road, skidding mainly depends on the coefficient of static
friction μs The coefficient of static friction
depends on the nature of the surface
which has a maximum limiting value. To avoid this problem, usually the outer
edge of the road is slightly raised compared to inner edge as shown in the
Figure 3.44. This is called banking of roads or tracks. This introduces an
inclination, and the angle is called banking angle.
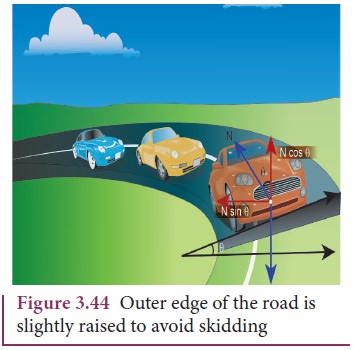
Let
the surface of the road make angle θ with horizontal surface. Then the normal force makes the
same angle θ with the
vertical. When the car takes a turn, there are two forces acting on the car:
a.
Gravitational
force mg (downwards)
b.
Normal
force N (perpendicular to surface)
We
can resolve the normal force into two components. N cosθ and N sinθ as shown in Figure 3.46. The
component N cosθ balances the downward gravitational
force ‘mg’ and component N sinθ will provide the necessary
centripetal acceleration. By using Newton second law
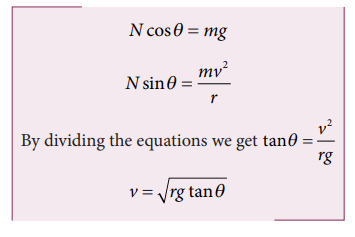
The
banking angle θ and radius of curvature of the road or track determines the
safe speed of the car at the turning. If the speed of car exceeds this safe
speed, then it starts to skid outward but frictional force comes into effect
and provides an additional centripetal force to prevent the outward skidding.
At the same time, if the speed of the car is little lesser than safe speed, it
starts to skid inward and frictional force comes into effect, which reduces
centripetal force to prevent inward skidding. However if the speed of the
vehicle is sufficiently greater than the correct speed, then frictional force
cannot stop the car from skidding.
Centrifugal Force
Circular
motion can be analysed from two different frames of reference. One is the
inertial frame (which is either at rest or in uniform motion) where Newton’s
laws are obeyed. The other is the rotating frame of reference which is a
non-inertial frame of reference as it is accelerating. When we examine the
circular motion from these frames of reference the situations are entirely
different. To use Newton’s first and second laws in the rotational frame of
reference, we need to include a pseudo force called ‘centrifugal force’. This
‘centrifugal force’ appears to act on the object with respect to rotating
frames. To understand the concept of centrifugal force, we can take a specific
case and discuss as done below.
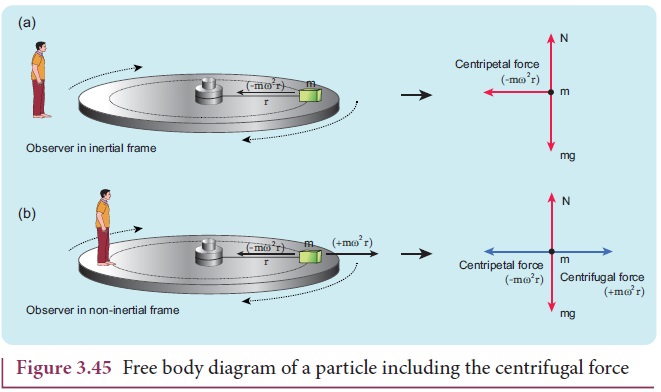
Consider
the case of a whirling motion of a stone tied to a string. Assume that the
stone has angular velocity ω in the inertial frame (at rest). If the motion of the stone
is observed from a frame which is also rotating along with the stone with same
angular velocity ω then, the stone appears to be at rest. This implies that in
addition to the inward centripetal force −mω2r there must be an equal and opposite force that acts on the
stone outward with value + mω2 r.
So the total force acting on the stone in a rotating frame is equal to zero (−mω 2 r + mω2r = 0). This outward force +mω2r is called the centrifugal force. The word ‘centrifugal’
means ‘flee from center’. Note that the ‘centrifugal force’ appears to act on
the particle, only when we analyse the motion from a rotating frame. With
respect to an inertial frame there is only centripetal force which is given by
the tension in the string. For this reason centrifugal force is called as a
‘pseudo force’. A pseudo force has no origin. It arises due to the non inertial
nature of the frame considered. When circular motion problems are solved from a
rotating frame of reference, while drawing free body diagram of a particle, the
centrifugal force should necessarily be included as shown in the Figure 3.45.
Effects of Centrifugal Force
Although
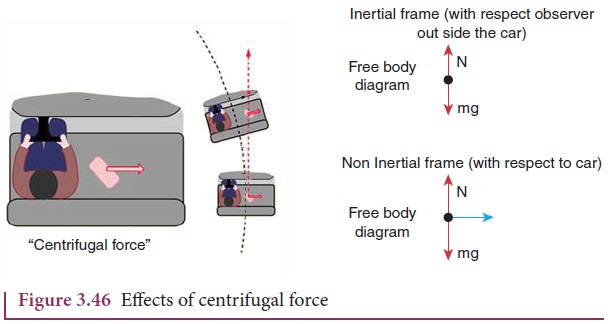
centrifugal force is a pseudo force, its effects are real. When a car takes a
turn in a curved road, person inside the car feels an outward force which
pushes the person away. This outward force is also called centrifugal force. If
there is sufficient friction between the person and the seat, it will prevent
the person from moving outwards. When a car moving in a straight line suddenly
takes a turn, the objects not fixed to the car try to continue in linear motion
due to their inertia of direction. While observing this motion from an inertial
frame, it appears as a straight line as shown in Figure 3.46. But, when it is
observed from the rotating frame it appears to move outwards.
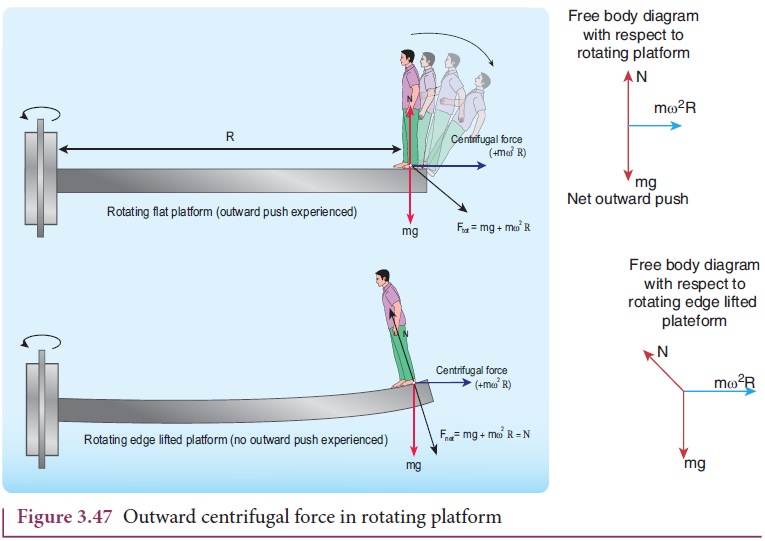
A
person standing on a rotating platform feels an outward centrifugal force and
is likely to be pushed away from the platform. Many a time the frictional force
between the platform and the person is not sufficient to overcome outward push.
To avoid this, usually the outer edge of the platform is little inclined
upwards which exerts a normal force on the person which prevents the person
from falling as illustrated in Figures 3.47.
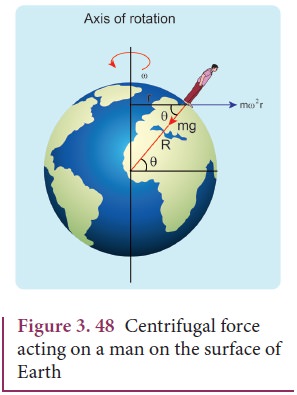
Centrifugal Force due to Rotation of the Earth
Even
though Earth is treated as an inertial frame, it is actually not so. Earth
spins about its own axis with an angular velocity ω. Any object on the surface of Earth (rotational frame)
experiences a centrifugal force. The centrifugal force appears to act exactly
in opposite direction from the axis of rotation. It is shown in the Figure
3.48.
The
centrifugal force on a man standing on the surface of the Earth is Fc = mω2r
where
r is perpendicular distance of the man from the axis of rotation. By using
right angle triangle as shown in the Figure 3.48, the distance r = R cos θ
Here
R = radius of the Earth
and
θ = latitude of the Earth where the man is standing.
Centripetal Force Versus Centrifugal Force
Salient
features of centripetal and centrifugal forces are compared in Table 3.4.

Solved Example Problems for Centripetal force
Example 3.22
If a stone of mass 0.25 kg tied to a string executes uniform circular motion with a speed of 2 m s-1 of radius 3 m, what is the magnitude of tensional force acting on the stone?
Solution
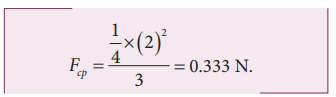
Example 3.23
The Moon orbits the Earth once in 27.3 days in an almost circular orbit. Calculate the centripetal acceleration experienced by the Earth? (Radius of the Earth is 6.4 × 106 m)
Solution
The centripetal acceleration is given by a = v2/r. This expression explicitly depends on Moon’s speed which is non trivial. We can work with the formula
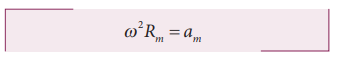
am is centripetal acceleration of the Moon due to Earth’s gravity.
ω is angular velocity.
Rm is the distance between Earth and the Moon, which is 60 times the radius of the Earth.

The centripetal acceleration of Moon towards the Earth is 0.00272 m s-2
Solved Example Problems for Vehicle on a leveled circular road
Example 3.24
Consider a circular leveled road of radius 10 m having coefficient of static friction 0.81. Three cars (A, B and C) are travelling with speed 7 ms-1, 8 m s-1 and 10 m s-1 respectively. Which car will skid when it moves in the circular level road? (g =10 m s-2)
Solution
From the safe turn condition the speed of the vehicle (v) must be less than or equal to
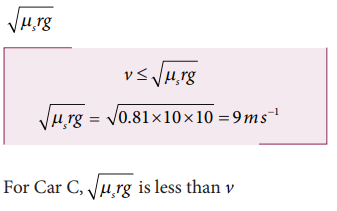
The speed of car A, B and C are 7 m s-1, 8 m s-1 and 10 m s-1 respectively. The cars A and B will have safe turns. But the car C has speed 10 m s-1 while it turns which exceeds the safe turning speed. Hence, the car C will skid.
Solved Example Problems for Banking of Tracks
Example 3.25
Consider a circular road of radius 20 meter banked at an angle of 15 degree. With what speed a car has to move on the turn so that it will have safe turn?
Solution
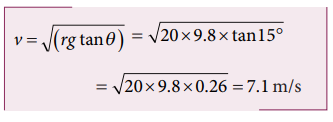
The safe speed for the car on this road is 7.1 m s-1
Solved Example Problems for Centrifugal Force due to Rotation of the Earth
Example 3.26
Calculate the centrifugal force experienced by a man of 60 kg standing at Chennai? (Given: Latitude of Chennai is 13°
Solution
The centrifugal force is given by Fc = mω2 R cosθ
The angular velocity (ω) of Earth = 2π/T.
where T is time period of the Earth (24 hours)

The radius of the Earth R = 6400 Km = 6400 × 103 m
Latitude of Chennai =13°
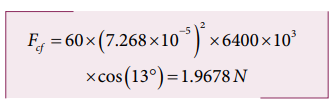
A 60 kg man experiences centrifugal force of approximately 2 Newton. But due to Earth’s gravity a man of 60 kg experiences a force =mg = 60 × 9.8 = 588N. This force is very much larger than the centrifugal force.
Related Topics