Physics - Friction | 11th Physics : UNIT 3 : Laws of Motion
Chapter: 11th Physics : UNIT 3 : Laws of Motion
Friction
FRICTION
Introduction
If
a very gentle force in the horizontal direction is given to an object at rest
on the table, it does not move. It is because of the opposing force exerted by
the surface on the object which resists its motion. This force is called the frictional force which always opposes the relative motion between an
object and the surface where it is placed. If the force applied is increased, the object moves after a certain limit.
Relative motion: when a force parallel to the surface is applied on the
object, the force tries to move the object with respect to the surface. This
‘relative motion’ is opposed
Frictional force always acts on the object parallel
to the surface on which the object is placed. There are two kinds of friction
namely 1) Static friction and 2) Kinetic friction.
Static Friction (vec fs→)
Static
friction is the force which opposes the initiation of motion of an object on
the surface. When the object is at rest on the surface, only two forces act on
it. They are the downward gravitational force and upward normal force. The
resultant of these two forces on the object is zero. As a result the object is
at rest as shown in Figure 3.23.
If
some external force Fext
is applied on the object parallel to the surface on which the object is at
rest, the surface exerts exactly an equal and opposite force on the object to
resist its motion and tries to keep the object at rest. It implies that
external force and frictional force are exactly equal and opposite. Therefore,
no motion parallel to the surface takes place. But if the external force is
increased, after a particular limit, the surface cannot provide sufficient
opposing frictional force to balance the external force on the object. Then the
object starts to slide. This is the maximal static friction that can be exerted
by the surface. Experimentally, it is found that the magnitude of static
frictional force fs
satisfies the following empirical relation.
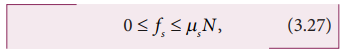
where
µs is the coefficient of static friction. It depends on the nature
of the surfaces in contact. N is normal force exerted by the surface on the
body and sometimes it is equal to mg. But it need not be equal to mg always.
Equation
(3.27) implies that the force of static friction can take any value from zero
to µsN.
If
the object is at rest and no external force is applied on the object, the
static friction acting on the object is zero ( fs = 0).
If
the object is at rest, and there is an external force applied parallel to the
surface, then the force of static friction acting on the object is exactly
equal to the external force applied on the object ( f s = Fext
). But still the static friction fs
is less than µsN.
When
object begins to slide, the static friction ( fs) acting on the object attains maximum,
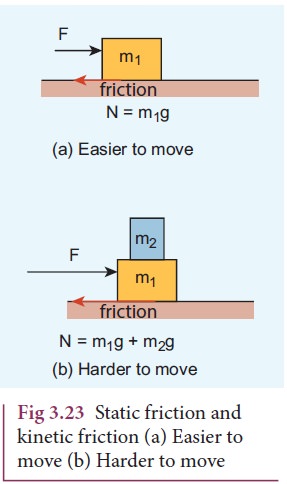
The static and kinetic frictions (which we discuss later) depend on the normal force acting on the object. If the object is pressed hard on the surface then the normal force acting on the object will increase. As a consequence it is more difficult to move the object. This is shown in Figure 3.23 (a) and (b). The static friction does not depend upon the area of contact.
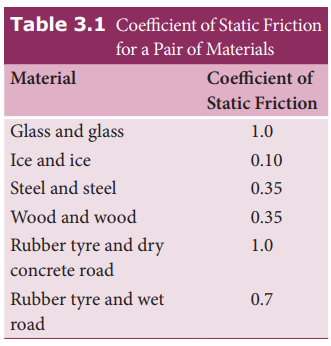
The values of coefficient of static friction for pairs of materials are presented in Table 3.1. Note that the ice and ice pair have very low coefficient of static friction. This means a block of ice can move easily over another block of ice.
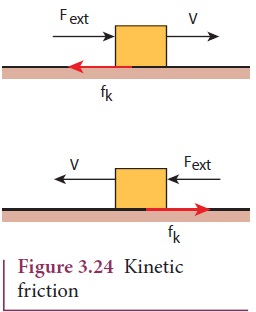
Kinetic Friction
If
the external force acting on the object is greater than maximum static
friction, the objects begin to slide. When an object slides, the surface exerts
a frictional force called kinetic
friction ![]() (also called sliding friction or dynamic friction). To move an
object at constant velocity we must apply a force which is equal in magnitude
and opposite to the direction of kinetic friction.
(also called sliding friction or dynamic friction). To move an
object at constant velocity we must apply a force which is equal in magnitude
and opposite to the direction of kinetic friction.
Experimentally
it was found that the magnitude of kinetic friction satisfies the relation
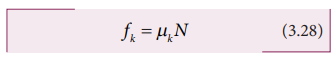
where
µk is the coefficient of
kinetic friction and N the normal force exerted by the surface on the object,
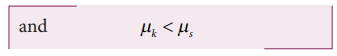
This
implies that starting of a motion is more difficult than maintaining it. The
salient features of static and kinetic friction are given in Table 3.2.

The
variation of both static and kinetic frictional forces with external applied
force is graphically shown in Figure 3.25.

The
Figure 3.25 shows that static friction increases linearly with external applied
force till it reaches the maximum. If the object begins to move then the
kinetic friction is slightly lesser than the maximum static friction. Note that
the kinetic friction is constant and it is independent of applied force.
To Move an Object - Push or pull? Which is easier?
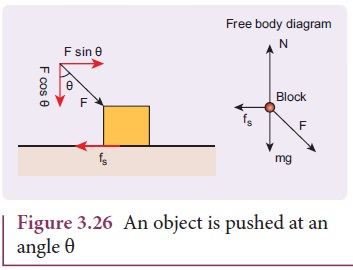
When
a body is pushed at an arbitrary angle θ (0 to π/2) , the applied force F
can be resolved into two components as F sinθ
parallel to the surface and F cosθ
perpendicular to the surface as shown in Figure 3.26. The total downward force
acting on the body is mg + Fcosθ. It implies that the normal force acting on the body increases. Since there is
no acceleration along the vertical direction the normal force N is equal to
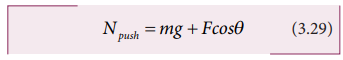
As
a result the maximal static friction also increases and is equal to
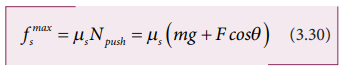
Equation
(3.30) shows that a greater force needs to be applied to push the object into
motion.
When
an object is pulled at an angle θ, the applied force is resolved into two
components as shown in Figure 3.27. The total downward force acting on the
object is
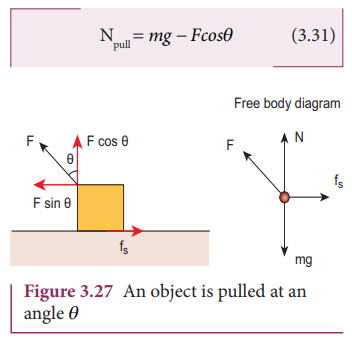
Equation
(3.31) shows that the normal force is less than Npush. From equations
(3.29) and (3.31), it is easier to pull an object than to push to make it move.
Angle of Friction
The
angle of friction is defined as the angle between the normal force (N) and the
resultant force (R) of normal force and maximum friction force ( fsmax )
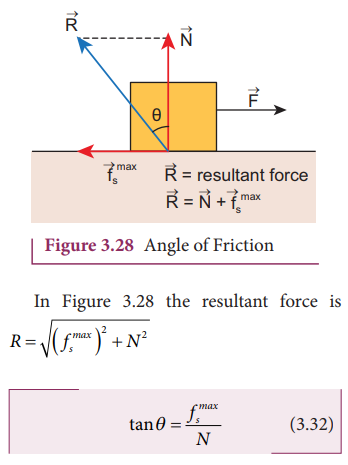
But
from the frictional relation, the object begins to slide when f smax
= µs N
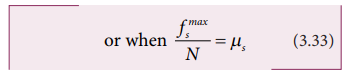
From
equations (3.32) and (3.33)
the coefficient of static friction is

The
coefficient of static friction is equal to tangent of the angle of friction
Angle of Repose
Consider
an inclined plane on which an object is placed, as shown in Figure 3.30. Let
the angle which this plane makes with the horizontal be θ . For small angles of θ , the object may not slide down. As
θ is
increased, for a particular value of θ , the object begins to slide down. This value is called
angle of repose. Hence, the angle of repose is the angle of inclined plane with
the horizontal such that an object placed on it begins to slide.

Let
us consider the various forces in action here. The gravitational force mg is
resolved into components parallel ( mg
sinθ) and
perpendicular (mg cosθ) to the inclined plane.
The
component of force parallel to the inclined plane (mg sinθ) tries to move the object down.
The
component of force perpendicular to the inclined plane (mg cosθ) is balanced by the Normal force (N).
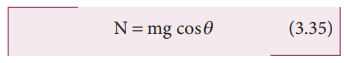
When the
object just begins
to move, the static friction attains its maximum value
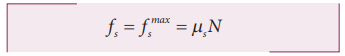
This
friction also satisfies the relation

Equating
the right hand side of equations (3.35) and (3.36), we get

From
the definition of angle of friction, we also know that

in
which θ is the
angle of friction.
Thus the angle of repose is the same as angle of friction. But the difference is that the angle of repose refers to inclined surfaces and the angle of friction is applicable to any type of surface.
Application of Angle of Repose
1.
Antilons make sand traps in such a way that when an insect enters the edge of
the trap, it starts to slide towards the bottom where the antilon hide itself.
The angle of inclination of sand trap is made to be equal to angle of repose. It
is shown in the Figure 3.30.

2.
Children are fond of playing on sliding board (Figure 3.31). Sliding will be
easier when the angle of inclination of the board is greater than the angle of
repose. At the same time if inclination angle is much larger than the angle of
repose, the slider will reach the bottom at greater speed and get hurt.
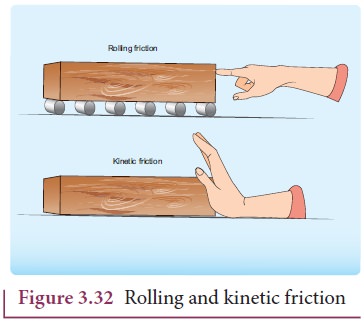
Rolling Friction
The
invention of the wheel plays a crucial role in human civilization. One of the
important applications is suitcases with rolling on coasters. Rolling wheels
makes it easier than carrying luggage. When an object moves on a surface,
essentially it is sliding on it. But wheels move on the surface through rolling
motion. In rolling motion when a wheel moves on a surface, the point of contact
with surface is always at rest. Since the point of contact is at rest, there is
no relative motion between the wheel and surface. Hence the frictional force is
very less. At the same time if an object moves without a wheel, there is a
relative motion between the object and the surface. As a result frictional
force is larger. This makes it difficult to move the object. The Figure 3.32
shows the difference between rolling and kinetic friction.
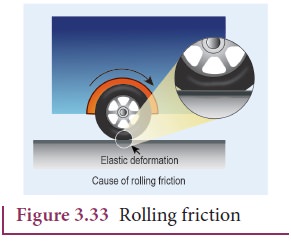
Ideally
in pure rolling, motion of the point of contact with the surface should be at
rest, but in practice it is not so. Due to the elastic nature of the surface at
the point of contact there will be some deformation on the object at this point
on the wheel or surface as shown in Figure 3.33. Due to this deformation, there
will be minimal friction between wheel and surface. It is called ‘rolling
friction’. In fact, ‘rolling friction’ is much smaller than kinetic friction.
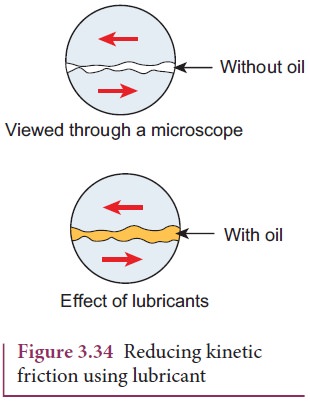
Methods to Reduce Friction
Frictional
force has both positive and negative effects. In some cases it is absolutely
necessary. Walking is possible because of frictional force. Vehicles (bicycle,
car) can move because of the frictional force between the tyre and the road. In
the braking system, kinetic friction plays a major role. As we have already
seen, the frictional force comes into effect whenever there is relative motion
between two surfaces. In big machines used in industries, relative motion
between different parts of the machine produce unwanted heat which reduces its
efficiency. To reduce this kinetic friction lubricants are used as shown in
Figure 3.34.
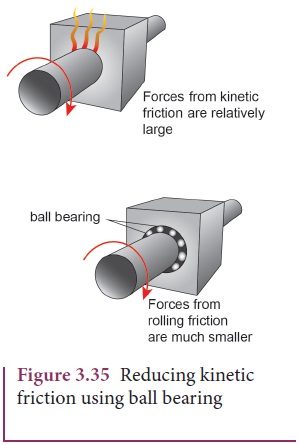
Ball
bearings provides another effective way to reduce the kinetic friction (Figure
3.35) in machines. If ball bearings are fixed between two surfaces, during the
relative motion only the rolling friction comes to effect and not kinetic
friction. As we have seen earlier, the rolling friction is much smaller than
kinetic friction; hence the machines are protected from wear and tear over the
years.
During
the time of Newton and Galileo, frictional force was considered as one of the
natural forces like gravitational force. But in the twentieth century, the
understanding on atoms, electron and protons has changed the perspective. The
frictional force is actually the electromagnetic force between the atoms on the
two surfaces. Even well polished surfaces have irregularities on the surface at
the microscopic level as seen in the Figure 3.36.

Solved Example Problems for Static Friction
Example 3.17
Consider an object of mass 2 kg resting on the floor. The coefficient of static friction between the object and the floor is µ s = 0.8. What force must be applied on the object to move it?
Solution
Since the object is at rest, the gravitational force experienced by an object is balanced by normal force exerted by floor.

Therefore to move the object the external force should be equal to maximum static friction.
Example 3.18
Consider an object of mass 50 kg at rest on the floor. A Force of 5 N is applied on the object but it does not move. What is the frictional force that acts on the object?
Solution
When the object is at rest, the external force and the static frictional force are equal and opposite.
The magnitudes of these two forces are equal, f s = Fext
Therefore, the static frictional force acting on the object is
Fs=5N
The direction of this frictional force is opposite to the direction of Fext .
Example 3.19
Two bodies of masses 7 kg and 5 kg are connected by a light string passing over a smooth pulley at the edge of the table as shown in the figure. The coefficient of static friction between the surfaces (body and table) is 0.9. Will the mass m1 = 7 kg on the surface move? If not what value of m2 should be used so that mass 7 kg begins to slide on the table?
Solution
As shown in the figure, there are four forces acting on the mass m1
a) Downward gravitational force along the negative y-axis (m1g)
b) Upward normal force along the positive y axis (N)
c) Tension force due to mass m2 along the positive x axis
d) Frictional force along the negative x axis
Since the mass m2 has no vertical motion, m1g = N
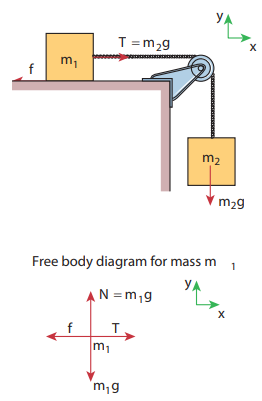
To determine whether the mass m1 moves on the surface, calculate the maximum static friction exerted by the table on the mass m1. If the tension on the mass m1 is equal to or greater than this maximum static friction, the object will move.
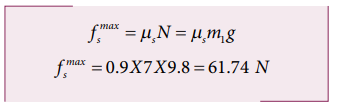
The tension T = m2 g = 5X9.8 = 49 N
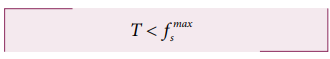
The tension acting on the mass m1 is less than the maximum static friction. So the mass m1 will not move.
To move the mass m1, T = fsmax where T = m2g

If the mass m2 is 6.3 kg then the mass m1 will begin to slide. Note that if there is no friction on the surface, the mass m1 will move for m2even for just 1 kg.
The values of coefficient of static friction for pairs of materials are presented in Table 3.1. Note that the ice and ice pair have very low coefficient of static friction. This means a block of ice can move easily over another block of ice.
Solved Example Problems for Angle of Repose
Example 3.20
A block of mass m slides down the plane inclined at an angle 60° with an acceleration g/2. Find the coefficient of kinetic friction?
Solution
Kinetic friction comes to play as the block is moving on the surface.
The forces acting on the mass are the normal force perpendicular to surface, downward gravitational force and kinetic friction fk along the surface.
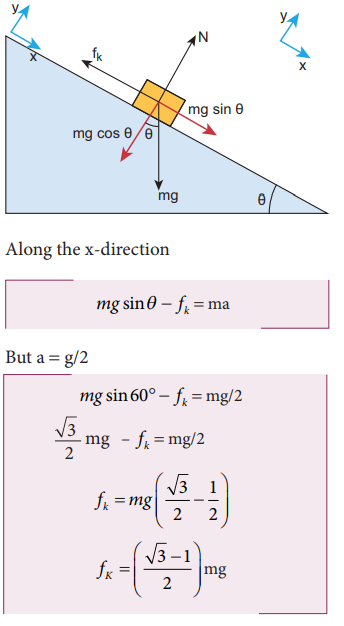
There is no motion along the y-direction as normal force is exactly balanced by the mg cosθ .
Solved Example Problems for Friction
Example 3.21
Consider an object moving on a horizontal surface with a constant velocity. Some external force is applied on the object to keep the object moving with a constant velocity. What is the net force acting on the object?
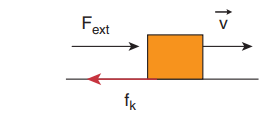
Solution
If an object moves with constant velocity, then it has no acceleration. According to Newton’s second law there is no net force acting on the object. The external force is balanced by the kinetic friction.
Related Topics