Centripetal force

Centripetal force

If a particle is in uniform circular motion, there must be centripetal acceleration towards the center of the circle. If there is acceleration then there must be some force acting on it with respect to an inertial frame. This force is called centripetal force.

As we have seen in chapter 2, the centripetal acceleration of a particle in the circular motion is given by a = v2/r and it acts r towards center of the circle. According to Newton’s second law, the centripetal force is given by

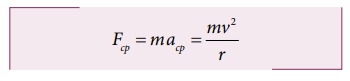
The word Centripetal force means center seeking force.

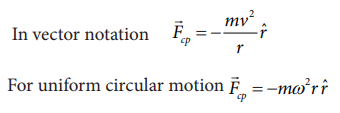
The direction -rˆ points towards the center of the circle which is the direction of centripetal force as shown in Figure 3.38.

It should be noted that ‘centripetal force’ is not other forces like gravitational force or spring force. It can be said as ‘force towards center’. The origin of the centripetal force can be gravitational force, tension in the string, frictional force, Coulomb force etc. Any of these forces can act as a centripetal force.

1. In the case of whirling motion of a stone tied to a string, the centripetal force on the particle is provided by the tensional force on the string. In circular motion in an amusement park, the centripetal force is provided by the tension in the iron ropes.

2. In motion of satellites around the Earth, the centripetal force is given by Earth’s gravitational force on the satellites. Newton’s second law for satellite motion is

Where r- distance of the planet from the center of the Earth.

3. When a car is moving on a circular track the centripetal force is given by the frictional force between the road and the tyres.

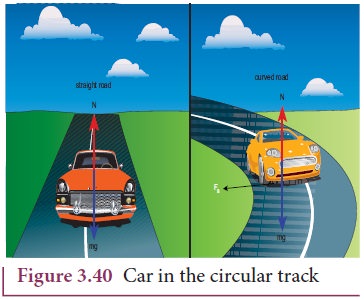
Newton’s second law for this case is

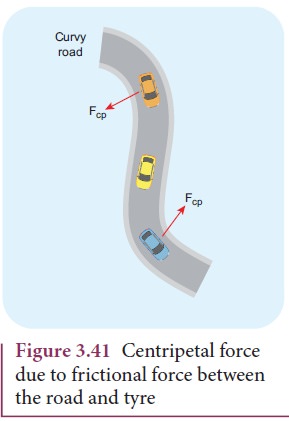
Even when the car moves on a curved track, the car experiences the centripetal force which is provided by frictional force between the surface and the tyre of the car. This is shown in the Figure 3.41.

4. When the planets orbit around the Sun, they experience centripetal force towards the center of the Sun. Here gravitational force of the Sun acts as centripetal force on the planets as shown in Figure 3.42.

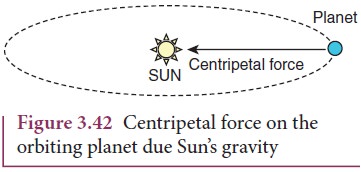
Newton’s second law for this motion

Gravitational force of Sun on the planet = mv2/r

Solved Example Problems for Centripetal force

Example 3.22

If a stone of mass 0.25 kg tied to a string executes uniform circular motion with a speed of 2 m s-1 of radius 3 m, what is the magnitude of tensional force acting on the stone?

Solution

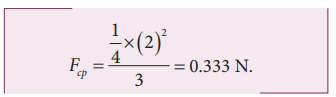
Example 3.23

The Moon orbits the Earth once in 27.3 days in an almost circular orbit. Calculate the centripetal acceleration experienced by the Earth? (Radius of the Earth is 6.4 Ã— 106 m)

Solution

The centripetal acceleration is given by a = v2/r.  This expression explicitly depends on Moon’s speed which is non trivial. We can work with the formula

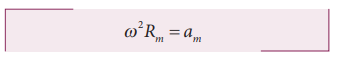
am is centripetal acceleration of the Moon due to Earth’s gravity.

ω is angular velocity.

Rm is the distance between Earth and the Moon, which is 60 times the radius of the Earth.

The centripetal acceleration of Moon towards the Earth is 0.00272 m s-2