Application of Newton’s Laws

APPLICATION OF NEWTON’S LAWS

Free Body Diagram

Free body diagram is a simple tool to analyse the motion of the object using Newton’s laws.

The following systematic steps are followed for developing the free body diagram:

·           Identify the forces acting on the object.

·           Represent the object as a point.

·           Draw the vectors representing the forces acting on the object.

When we draw the free body diagram for an object or a system, the forces exerted by the object should not be included in the free body diagram.

Example 3.1

A book of mass m is at rest on the table.

1) What are the forces acting on the book?

2) What are the forces exerted by the book? (3) Draw the free body diagram for the book.

Solution

1) There are two forces acting on the book.

i. Gravitational force (mg) acting downwards on the book

ii. Normal contact force (N) exerted by the surface of the table on the book. It acts upwards as shown in the figure.

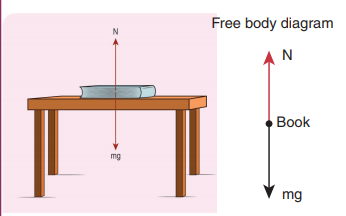
2) According to Newton’s third law, there are two reaction forces exerted by the book.

i. The book exerts an equal and opposite force (mg) on the Earth which acts upwards.

ii. The book exerts a force which is equal and opposite to normal force on the surface of the table (N) acting downwards.

3) The free body diagram of the book is shown in the figure.

Example 3.2

If two objects of masses 2.5 kg and 100 kg experience the same force 5 N, what is the acceleration experienced by each of them?

Solution

From Newton’s second law (in magnitude form), F = ma

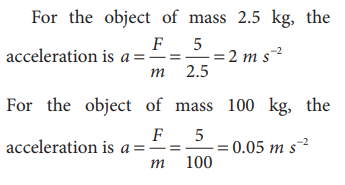
When an apple falls, it experiences Earth’s gravitational force. According to Newton’s third law, the apple exerts equal and opposite force on the Earth. Even though both the apple and Earth experience the same force, their acceleration is different. The mass of Earth is enormous compared to that of an apple. So an apple experiences larger acceleration and the Earth experiences almost negligible acceleration. Due to the negligible acceleration, Earth appears to be stationary when an apple falls.

Example 3.3

Which is the greatest force among the three force  shown below

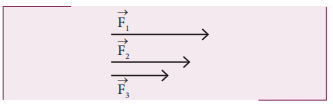
Solution

Force is a vector and magnitude of the vector is represented by the length of the vector. Here has greater length compared to other two. So  is largest of the three.

Example 3.4

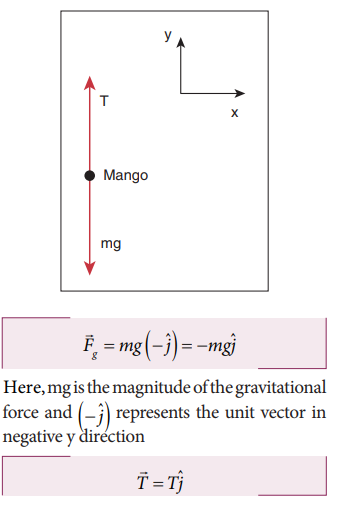
Apply Newton’s second law to a mango hanging from a tree. (Mass of the mango is 400 gm)

Solution

Note: Before applying Newton’s laws, the following steps have to be followed:

1. Choose a suitable inertial coordinate system to analyse the problem. For most of the cases we can take Earth as an inertial coordinate system.

2. Identify the system to which Newton’s laws need to be applied. The system can be a single object or more than one object.

3. Draw the free body diagram.

4. Once the forces acting on the system are identified, and the free body diagram is drawn, apply Newton’s second law. In the left hand side of the equation, write the forces acting on the system in vector notation and equate it to the right hand side of equation which is the product of mass and acceleration. Here, acceleration should also be in vector notation.

5. If acceleration is given, the force can be calculated. If the force is given, acceleration can be calculated.

By following the above steps:

We fix the inertial coordinate system on the ground as shown in the figure.

The forces acting on the mango are

i. Gravitational force exerted by the Earth on the mango acting downward along negative y axis

ii. Tension (in the cord attached to the mango) acts upward along positive y axis.

The free body diagram for the mango is shown in the figure

Example 3.5

A person rides a bike with a constant velocity  with respect to ground and another biker accelerates with acceleration with respect to ground. Who can apply Newton’s second law with respect to a stationary observer on the ground?

Solution

Second biker cannot apply Newton’s second law, because he is moving with acceleration with respect to Earth (he is not in inertial frame). But the first biker can apply Newton’s second law because he is moving at constant velocity with respect to Earth (he is in inertial frame).

Example 3.6

The position vector of a particle is given  which the particle experiences net force?

Solution

Here, the particle has acceleration only along positive y direction. According to Newton’s second law, net force must also act along positive y direction. In addition, the particle has constant velocity in positive x direction and no velocity in z direction. Hence, there are no net force along x or z direction.

Example 3.7

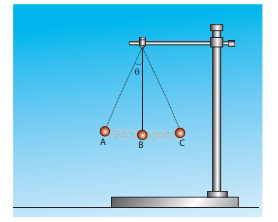
Consider a bob attached to a string, hanging from a stand. It oscillates as shown in the figure.

Solution

a)                 Identify the forces that act on the bob?

b)                b)  What is the acceleration experienced by the bob?

Two forces act on the bob.

(i) Gravitational force (mg) acting downwards

(ii) Tension (T) exerted by the string on the bob, whose position determines the direction of T as shown in figure.

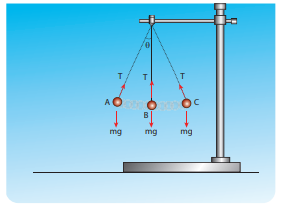
The bob is moving in a circular arc as shown in the above figure. Hence it has centripetal acceleration. At a point A and C, the bob comes to rest momentarily and then its velocity increases when it moves towards point B. Hence, there is a tangential acceleration along the arc. The gravitational force can be resolved into two components (mg cosθ, mg sinθ) as shown below

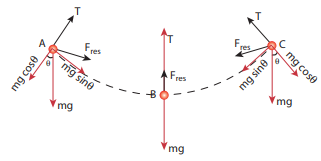
Example 3.8

The velocity of a particle moving in a plane is given by the following diagram. Find out the direction of force acting on the particle?

Solution

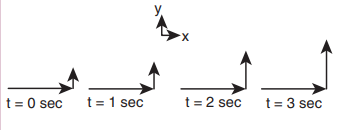
The velocity of the particle is 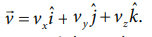 As shown in the figure, the particle is moving in the xy plane, there is no motion in the z direction. So velocity in the z direction is zero (vz = 0). The velocity of the particle has x component (vx) and y component (v y). From figure, as time increases from t = 0 sec to t = 3 sec, the length of the vector in y direction is changing (increasing). It means component of velocity ( vy ) is increasing with respect to time. According to Newton’s second law, if velocity changes with respect to time then there must be acceleration. In this case, the particle has acceleration in the y direction since the y component of velocity changes. So the particle experiences force in the y direction. The length of the vector in x direction does not change. It means that the particle has constant velocity in the x direction. So no force or zero net force acts in the x direction.

Example 3.9

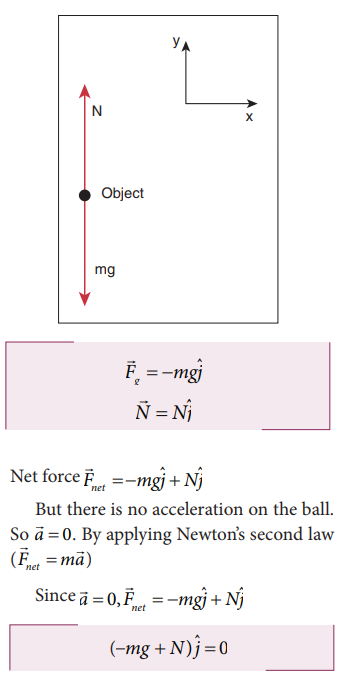
Apply Newton’s second law for an object at rest on Earth and analyse the result.

Solution

The object is at rest with respect to Earth (inertial coordinate system). There are two forces that act on the object.

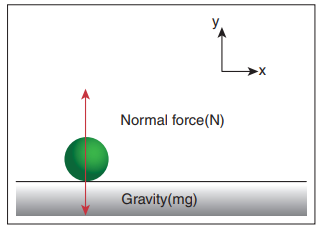
i. Gravity acting downward (negative y-direction)

ii. Normal force by the surface of the Earth acting upward (positive y-direction)

The free body diagram for this object is

By comparing the components on both sides of the equation, we get

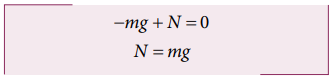
We can conclude that if the object is at rest, the magnitude of normal force is exactly equal to the magnitude of gravity.

 Example 3.11

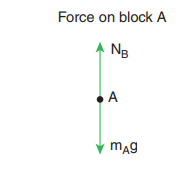
Identify the forces acting on blocks A, B and C shown in the figure.

Solution

Forces on block A:

i. Downward gravitational force exerted by the Earth (mAg)

ii. Upward normal force (NB) exerted by block B (NB)

The free body diagram for block A is as shown in the following picture.

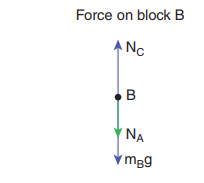
Forces on block B :

i. Downward gravitational force exerted by Earth (mBg)

ii. Downward force exerted by block A (NA)

iii. Upward normal force exerted by block C (NC)

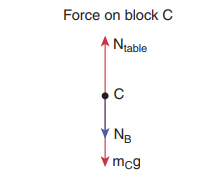
Forces onblock C:

i. Downward gravitational force exerted by Earth (mCg)

ii. Downward force exerted by block B (NB)

iii. Upward force exerted by the table (Ntable)

Example 3.12

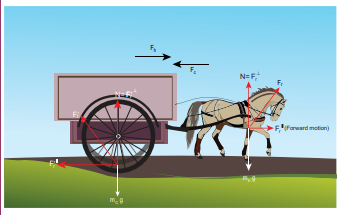
Consider a horse attached to the cart which is initially at rest. If the horse starts walking forward, the cart also accelerates in the forward direction. If the horse pulls the cart with force Fh in forward direction, then according to Newton’s third law, the cart also pulls the horse by equivalent opposite force Fc = Fh in backward direction. Then total force on ‘cart+horse’ is zero. Why is it then the ‘cart+horse’ accelerates and moves forward?

Solution

This paradox arises due to wrong application of Newton’s second and third laws. Before applying Newton’s laws, we should decide ‘what is the system?’. Once we identify the ‘system’, then it is possible to identify all the forces acting on the system. We should not consider the force exerted by the system. If there is an unbalanced force acting on the system, then it should have acceleration in the direction of the resultant force. By following these steps we will analyse the horse and cart motion.

If we decide on the cart+horse as a ‘system’, then we should not consider the force exerted by the horse on the cart or the force exerted by cart on the horse. Both are internal forces acting on each other. According to Newton’s third law, total internal force acting on the system is zero and it cannot accelerate the system. The acceleration of the system is caused by some external force. In this case, the force exerted by the road on the system is the external force acting on the system. It is wrong to conclude that the total force acting on the system (cart+horse) is zero without including all the forces acting on the system. The road is pushing the horse and cart forward with acceleration. As there is an external force acting on the system, Newton’s second law has to be applied and not Newton’s third law.

The following figures illustrates this.

If we consider the horse as the ‘system’, then there are three forces acting on the horse.

i. Downward gravitational force (mh g )

ii. Force exerted by the road (Fr )

iii. Backward force exerted by the cart (Fc )

It is shown in the following figure.

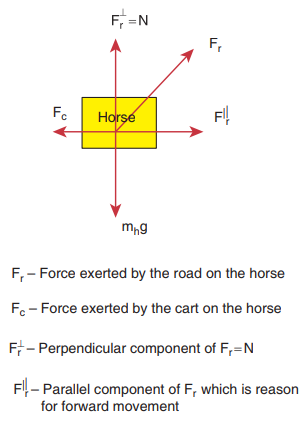
The force exerted by the road can be resolved into parallel and perpendicular components. The perpendicular component balances the downward gravitational force. There is parallel component along the forward direction. It is greater than the backward force (Fc ). So there is net force along the forward direction which causes the forward movement of the horse.

If we take the cart as the system, then there are three forces acting on the cart.

i. Downward gravitational force (mc g)

ii. Force exerted by the road ( Fr’ )

iii. Force exerted by the horse (Fh )

It is shown in the figure

The force exerted by the road (  ) can be resolved into parallel and perpendicular components. The perpendicular component cancels the downward gravity (mc g). Parallel component acts backwards and the force exerted by the horse () acts forward. Force () is greater than the parallel component acting in the opposite direction. So there is an overall unbalanced force in the forward direction which causes the cart to accelerate forward.

If we take the cart+horse as a system, then there are two forces acting on the system.

i. Downward gravitational force (mh + mc)g

ii. The force exerted by the road (Fr ) on the system.

It is shown in the following figure.

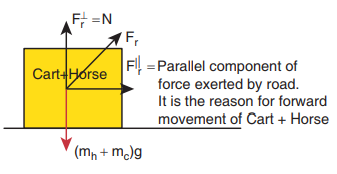
(iii) In  this case  the  force  exerted by the road (Fr ) on the system (cart+horse) is resolved in to parallel and perpendicular components. The perpendicular component is the normal force which cancels the downward gravitational force (mh + mc)g. The parallel component of the force is not balanced, hence the system (cart+horse) accelerates and moves forward due to this force.

Example 3.13

The position of the particle is represented by y = ut â€“ 1/2  gt2 .

a) What is the force acting on the particle?

b) What is the momentum of the particle?

Solution

To find the force, we need to find the acceleration experienced by the particle.

The momentum of the particle = mv = m (u-gt).

The force acting on the object is given by F = ma = −mg

The negative sign implies that the force is acting on the negative y direction. This is exactly the force that acts on the object in projectile motion.

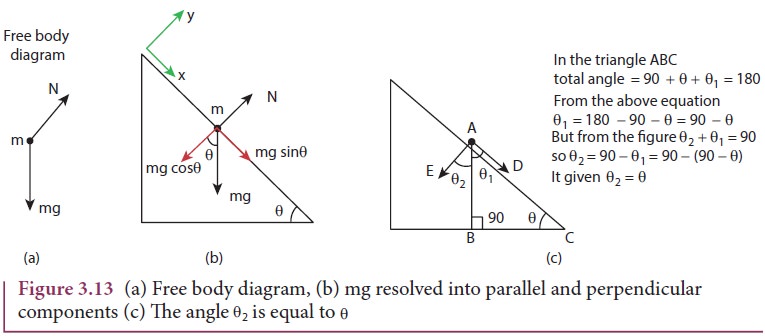
Particle Moving in an Inclined Plane

When an object of mass m slides on a frictionless surface inclined at an angle θ as shown in the Figure 3.12, the forces acting on it decides the

a.        acceleration of the object

b.        speed of the object when it reaches the bottom

The force acting on the object is

(i)  Downward gravitational force (mg)

(ii)  Normal force perpendicular to inclined surface (N)

To draw the free body diagram, the block is assumed to be a point mass (Figure 3.13 (a)). Since the motion is on the inclined surface, we have to choose the coordinate system parallel to the inclined surface as shown in Figure 3.13 (b).

The gravitational force mg is resolved in to parallel component mg sinθ along the inclined plane and perpendicular component mg cosθ perpendicular to the inclined surface (Figure 3.13 (b)).

Note that the angle made by the gravitational force (mg) with the perpendicular to the surface is equal to the angle of inclination θ as shown in Figure 3.13 (c).

There is no motion(acceleration) along the y axis. Applying Newton’s second law in the y direction

By comparing the components on both sides, N − mg cosθ = 0

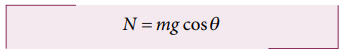
The magnitude of normal force (N) exerted by the surface is equivalent to mg cosθ .

The object slides (with an acceleration) along the x direction. Applying Newton’s second law in the x direction

Note that the acceleration depends on the angle of inclination θ . If the angle θ is 90 degree, the block will move vertically with acceleration a = g.

Newton’s kinematic equation is used to find the speed of the object when it reaches the bottom. The acceleration is constant throughout the motion.

The acceleration a is equal to mg sinθ. The initial speed (u) is equal to zero as it starts from rest. Here s is the length of the inclined surface.

The speed (v) when it reaches the bottom is (using equation (3.3))

Two Bodies in Contact on a Horizontal Surface

Consider two blocks of masses m₁ and m₂ (m₁ > m₂) kept in contact with each other on a smooth, horizontal frictionless surface as shown in Figure 3.14.

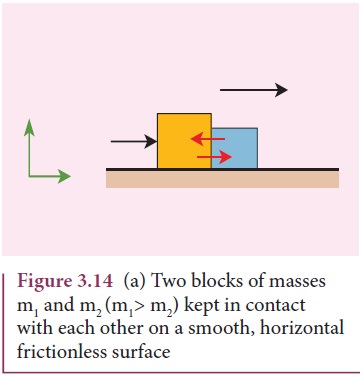
By the application of a horizontal force F, both the blocks are set into motion with acceleration ‘a’ simultaneously in the direction of the force F.

To find the acceleration  , Newton’s second law has to be applied to the system (combined mass m = m₁ + m₂)

The force exerted by the block m₁ on m₂ due to its motion is called force of contact . According to Newton’s third law, the block m ₂ will exert an equivalent opposite reaction force  on block m₁.

Figure 3.14 (b) shows the free body diagram of block m_1.

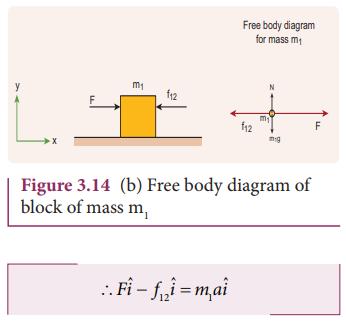
By comparing the components on both sides of the above equation, we get

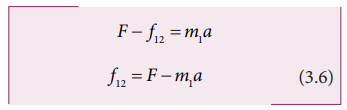
Substituting the value of acceleration from equation (3.5) in (3.6) we get

Equation (3.7) shows that the magnitude of contact force depends on mass m₂ which provides the reaction force. Note that this force is acting along the negative x direction.

In vector notation, the reaction force on mass m1 is given by

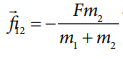
For mass m₂ there is only one force acting on it in the x direction and it is denoted by  This force is exerted by mass m₁. The free body diagram for mass m₂ is shown in Figure 3.14 (c).

By comparing the components on both sides of the above equation

Applying Newton’s second law for mass m2

f₂₁iˆ = m₂aiˆ

Motion of Connected Bodies

When objects are connected by strings and a force F is applied either vertically or horizontally or along an inclined plane, it produces a tension T in the string, which affects the acceleration to an extent. Let us discuss various cases for the same.

Case 1: Vertical motion

Consider two blocks of masses m₁ and m₂ (m₁> m₂) connected by a light and inextensible string that passes over a pulley as shown in Figure 3.15.

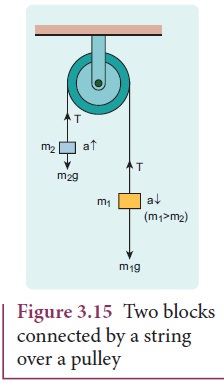
Let the tension in the string be T and acceleration a. When the system is released, both the blocks start moving, m₂ vertically upward and m₁ downward with same acceleration a. The gravitational force m₁g on mass m₁ is used in lifting the mass m₂.

The upward direction is chosen as y direction. The free body diagrams of both masses are shown in Figure 3.16.

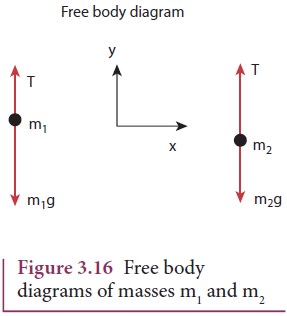
Applying Newton’s second law for mass m₂

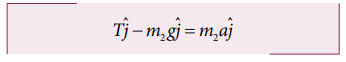
The left hand side of the above equation is the total force that acts on m₂ and the right hand side is the product of mass and acceleration of m₂ in y direction.

By comparing the components on both sides, we get

By comparing the components on both sides, we get

This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest.

To find the tension acting on the string, substitute the acceleration from the equation (3.12) into the equation (3.9).

By taking m₂g common in the RHS of equation (3.13)

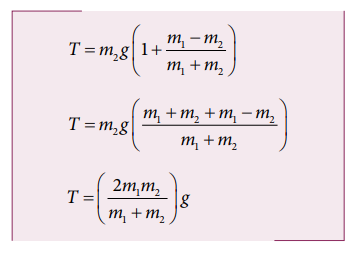
Equation (3.12) gives only magnitude of acceleration.

Case 2: Horizontal motion

In this case, mass m₂ is kept on a horizontal table and mass m₁ is hanging through a small pulley as shown in Figure 3.17. Assume that there is no friction on the surface.

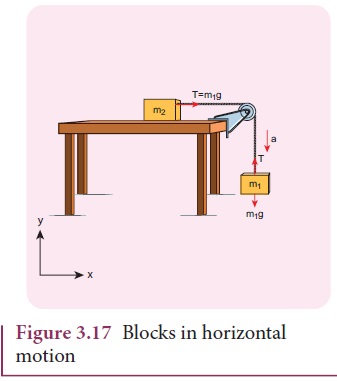
As both the blocks are connected to the unstretchable string, if m₁ moves with an acceleration a downward then m₂ also moves with the same acceleration a horizontally.

The forces acting on mass m₂ are

i.               Downward gravitational force (m₂g)

ii.               Upward normal force (N) exerted by the surface

iii.               Horizontal tension (T) exerted by the string

The forces acting on mass m₁ are

i.               Downward gravitational force (m₁g)

ii.               Tension (T) acting upwards

The free body diagrams for both the masses is shown in Figure 3.18.

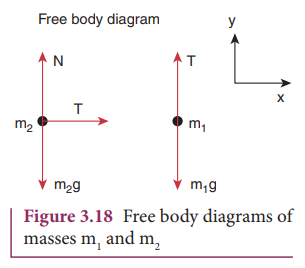
Applying Newton’s second law for m₁

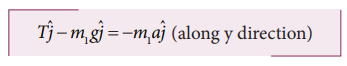
By comparing the components on both sides of above equation,

By comparing the components on both sides of above equation,

Tension in the string can be obtained by substituting equation  (3.17) in equation (3.15)

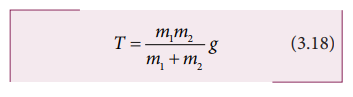
Comparing motion in both cases, it is clear that the tension in the string for horizontal motion is half of the tension for vertical motion for same set of masses and strings.

This result has an important application in industries. The ropes used in conveyor belts (horizontal motion) work for longer duration than those of cranes and lifts (vertical motion).

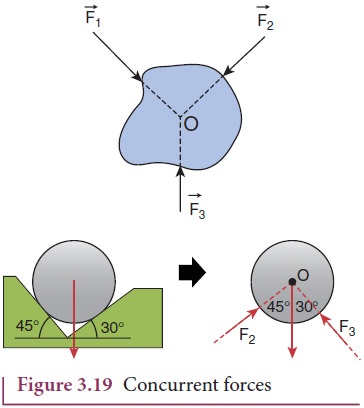
Concurrent Forces and Lami’s Theorem

A collection of forces is said to be concurrent, if the lines of forces act at a common point. Figure 3.19 illustrates concurrent forces.

Concurrent forces need not be in the same plane. If they are in the same plane, they are concurrent as well as coplanar forces.