Chapter: 11th Physics : UNIT 3 : Laws of Motion
Solved Example Problems for Physics: Laws of Motion
Numerical Problems
1. A force of 50N act on the object of mass 20 kg. shown in the figure. Calculate the acceleration of the object in x and y directions.
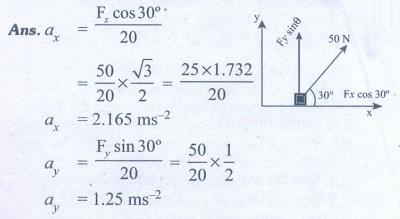
Ans: ax=2.165 ms-2; ay=1.25 ms-2
2. A spider of mass 50 g is hanging on a string of a cob web as shown in the figure. What is the tension in the string?

Answer:
T
= mg
Mass
(m) = 50g = 0.050 kg
g
= 9.8 ms-2
T
= 0.050 × 9.8
= 0.49 N.
Ans: T=0.49N
3. What is the reading shown in spring balance?

Answer:
Zero,
9.8 N. The weight of the body is equal to the acceleration due to gravity.
Ans: Zero, 9.8 N
4. The physics books are stacked on each other in the sequence: +1 volumes 1 and 2; +2 volumes 1 and 2 on a table.
a. Identify the forces acting on each book and draw the free body diagram.
b. Identify the forces exerted by each book on the other.
Answer:
(i)
Gravitation force mg acting downwards
on the books +1 vol. 1, vol. 2, +2. vol. 1, +2 vol. 2.
(ii)
Upward normal force (NB) exerted by book B(NB).
(iii)
Normal contact force (N) exerted by the vol. 2 on the book vol. 1 and so on.
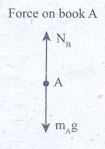
Forces on book A:
(i)
Downward gravitational force exerted by the Earth (mAg)
(ii)
Upward normal force (NB) exerted by book B (NB)
The
free body diagram for book A is as shown in the following picture.
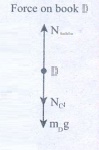
Force on book B
(i)
Downward gravitational force exerted by Earth (mBg)
(ii)
Downward force exerted by book A (NA)
(iii)Upward
normal force exerted by book C (Nc)

Forces oil book C:
(i)
Downward gravitational force exerted by Earth (mcg)
(ii)
Downward force exerted by book B(NB)
(iii)
Upward normal force exerted by the book (ND)

Forces on book D:
(i)
Downward gravitational force exerted by Earth (mDg)
(ii)
Downward force exerted by book C (Nc)
(iii) Upward force exerted by the table (Ntable)
5. A bob attached to the string oscillates back and forth. Resolve the forces acting on the bob in to components. What is the acceleration experience by the bob at an angle θ.
Answer:
(i)
The radial force = T - mg cos θ provides centripetal force but no torque about
support O.
(ii)
The tangential force mg sin θ provide
the restoring torque.
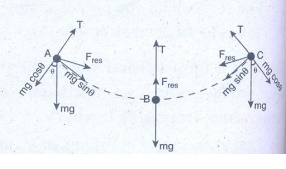
Tangential
acceleration α = tangential force/ m
=
g sin θ
Centripetal
acceleration = T – mg cos θ / m
Ans: Tangential acceleration = g sinθ ; centripetal acceleration = (T−mg cosθ)/m
6. Two masses m1 and m2 are connected with a string passing over a frictionless pulley fixed at the corner of the table as shown in the figure. The coefficient of static friction of mass m1 with the table is μs. Calculate the minimum mass m3 that may be placed on m1to prevent it from sliding. Check if m1=15 kg, m2=10 kg, m3=25 and μs =0.2
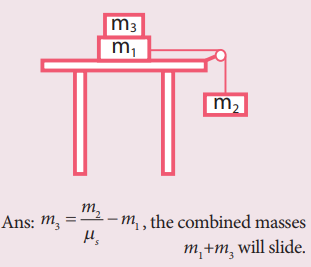
Answer:
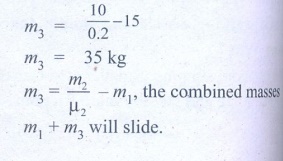
7. Calculate the acceleration of the bicycle of mass 25 kg as shown in Figures 1 and 2.
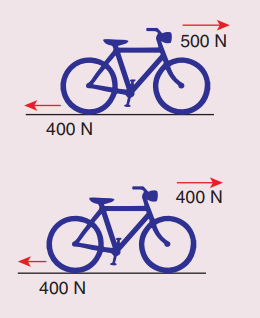
Answer
(i)
Net force F1 = 500 - 400 = 100 N
Mass
m = 25 kg; a = ?
Acceleration
a = F/ m
a = 100/ 25 = 4
ms-2
(ii)
Net force acting on cycle F2 = 400 - 400 = 0.
a = 0.
Ans: a=4 ms-2, zero
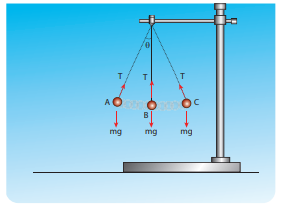
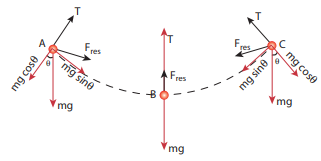
8. Apply Lami’s theorem on sling shot and calculate the tension in each string ?
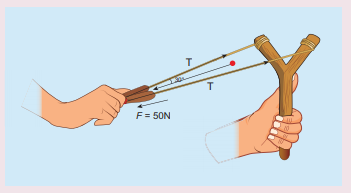
Answer:
Force F = mg = 50 N;
θ = 30 °
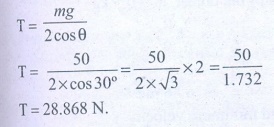
T= 28.868 N.
Ans: T= 28.868N.
9. A football player kicks a 0.8 kg ball and imparts it a velocity 12 ms-1. The contact between the foot and ball is only for one- sixtieth of a second. Find the average kicking force.
Answer:
Time
of contact = 1/60 s
Mass
of ball = 0.8 kg.
Velocity
v = 12 ms-1
Average
force = Δp/Δt
Favg
= 0.8x12 / (1/60)
=
0.8 × 12 × 60 = 576 N .
Average
kicking force = 576 N.
Ans: 576N.
10. A stone of mass 2 kg is attached to a string of length 1 meter. The string can withstand maximum tension 200 N. What is the maximum speed that stone can have during the whirling motion?
Answer:
Length,
r = 1 m
Mass = 2 kg
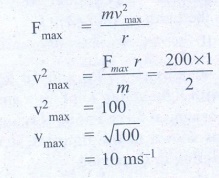
Ans: vmax=10ms-1
11. Imagine that the gravitational force between Earth and Moon is provided by an invisible between the Moon and Earth. What is the tension that exists in this invisible string due to Earth’s centripetal force?
(Mass of the Moon = 7.34 × 1022 kg, Distance between Moon and Earth = 3.84 × 108 m)
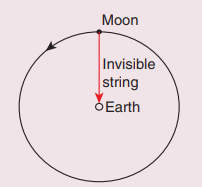
Answer
Tension
T = Centripetal force
Centripetal
force F = m × Centripetal acceleration
F
= m × 0.00272
=
7.34 × 1022 × 0.00272 = 0.0199 × 1022
=
1.99 × 1020 = 2 × 1020N.
(i)
The centripetal acceleration is given by a = v2/r. This
expression explicitly depends on Moon’s speed which is non-trivial. We can work
with the formula
ω2Rm = am
(ii)
am is centripetal acceleration of the Moon due to Earth’s gravity,
ω
is angular velocity.
(iii)
Rm is the distance between
Earth and the Moon, which is 60 times the radius of the Earth
Rm
= 60R = 60 × 6.4 × 106 = 384 × 106 m.
(iv)
As we know the angular velocity ω = 2π/T and T = 27.3 days = 27.3 × 24 × 60 ×
60 second = 2.358 × 106 sec. By substituting these values in the
formula for acceleration
am
= (4π2)(384×106) / (2.358×106)2 =
0.00272 ms-2.
The
centripetal acceleration of Moon towards the Earth is 0.00272 ms-2.
T
~ 2 × 1020N
Ans: T = 2 x 1020 N.
12. Two bodies of masses 15 kg and 10 kg are connected with light string kept on a smooth surface. A horizontal force F=500 N is applied to a 15 kg as shown in the figure. Calculate the tension acting in the string
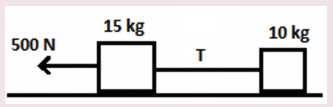
Answer:

Ans: T = 200N .
13. People often say “For every action there is an equivalent opposite reaction”. Here they meant ‘action of a human’. Is it correct to apply Newton’s third law to human actions? What is mean by ‘action’ in Newton third law? Give your arguments based on Newton’s laws.
Answer:
Newton’s
third law is applicable to only human’s actions which involves physical force.
Third law is not applicable to human’s psychological! actions or thoughts.
Ans: Newton’s third law is applicable to only human’s actions which involves physical force. Third law is not applicable to human’s psychological actions or thoughts
14. A car takes a turn with velocity 50 m s-1 on the circular road of radius of curvature 10 m. calculate the centrifugal force experienced by a person of mass 60kg inside the car?
Answer:
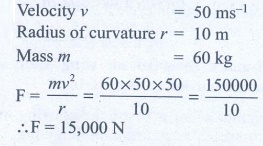
Ans: 15,000 N
15. A long stick rests on the surface. A person standing 10 m away from the stick. With what minimum speed an object of mass 0.5 kg should he thrown so that it hits the stick. (Assume the coefficient of kinetic friction is 0.7).
Ans: 11.71 m s-1

Conceptual Questions
1. Why it is not possible to push a car from inside?
Answer:
(i)
When you push a car from inside, the reaction force of your pushing is balanced
out by your body moving backward.
(ii)
The seat behind you pushes against to bring things to static equilibrium.
2. There is a limit beyond which the polishing of a surface increases frictional resistance rather than decreasing it why?
Answer:
(i)
Due to excessive polishing, more molecules of the two surfaces come closer.
Thus they form more bonds and offer great resistances.
(ii)
Because friction arises due to molecular adhesion i.e. due to electrostatic
forces.
3. Can a single isolated force exist in nature? Explain your answer.
Answer:
No,
a single isolated force cannot exist in nature because it violates the Newton's
third law.
4. Why does a parachute descend slowly?
Answer:
A
parachute is a device used to slow down on object that is falling towards the
ground. When the parachute opens, the air resistance increases. So the person
can land safely.
5. When walking on ice one should take short steps. Why?
Answer:
It
is to avoid slipping. Smaller step causes more normal force and thereby more
friction.
6. When a person walks on a surface, the frictional force exerted by the surface on the person is opposite to the direction of motion. True or false?
Answer:
False.
The frictional force exerted by the surface is not opposite to the direction of
motion.
7. Can the coefficient of friction be more than one?
Answer:
Yes,
μ > 1, friction is stronger than normal force.
8. Can we predict the direction of motion of a body from the direction of force on it?
Answer
In
free body diagrams, the force of friction is always parallel to the surface of
contact. The force of kinetic friction is always opposite the direction of
motion.
9. The momentum of a system of particles is always conserved. True or false?
Answer:
True.
The momentum of a system of particles is always conserved.
SOLVED EXAMPLE
1. A body of mass 100 kg is moving with an acceleration of 50 cm s-2. Calculate the force experienced by it.
Solution:
Mass m = 100 kg
Acceleration a = 50 cm s-2 = 0.5 m s-2
Using Newton’s second law,

2.Identify the free body diagram that represents the particle accelerating in positive x direction in the following.
The relative magnitude of forces should be indicated when the free body diagram for mass m is drawn.
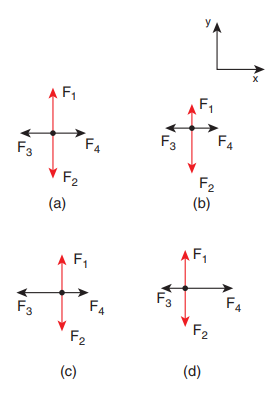
Case (a):
The forces F1 and F2 have equal length but opposite direction. So net force along y-direction is zero. Since the force is zero, acceleration is also zero along Y-direction (Newton’s second law). Similarly in the x direction, F3 and F4 have equal length and opposite in direction. So net force is zero in the x direction. So there is no acceleration in x direction.
Case (b):
The forces F1 and F2 are not equal in length and act opposite to each other. The figure (b) shows that there are unbalanced forces along the y-direction. So the particle has acceleration in the -y direction. The forces F3 and F4 are having equal length and act in opposite directions. So there is no net force along the x direction. So the particle has no acceleration in the x direction.
Case (c):
The forces F1 and F2 are equal in magnitude and act opposite to each other. The net force is zero in y direction. So in y-direction there is no acceleration. The forces F3 and F4 are not equal in magnitude and F3 is greater than F4 . So there is a net acceleration in negative x direction
Case (d):
The forces F1 and F2 are equal in magnitude and act opposite to each other. The net force is zero in y direction. So there is no acceleration in y-direction. The forces F3 and F4 are not equal in magnitude. The force F4 is greater than the force F3. So there is a net acceleration in the positive x direction.
3. A gun weighing 25 kg fires a bullet weighing 30 g with the speed of 200 ms-1. What is the speed of recoil of the gun.
Solution:
Mass of the gun M = 25 kg
Mass of the bullet m = 30 g = 30 × 10-3
kg Speed of bullet v = 200 m s-1
Speed of gun V = ?
The motion is in one dimension.
As per law of conservation of momentum,

The negative sign shows that the gun moves in the opposite direction of the bullet. Further the magnitude of the recoil speed is very small compared to the bullet’s speed.
4. A wooden box is lying on an inclined plane. What is the coefficient of friction if the box starts sliding when the angle of inclination is 45°.
Solution:
Angle of inclination Θ = 45°
Coefficient of friction µ = tan Θ = tan 45° = 1
5. Two masses m1 = 5 kg and m2 = 4 kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of each mass when left free to move? (g = 10ms-2)

6. A block of mass m is pushed momentarily along a horizontal surface with an initial velocity u. If µk is the coefficient of kinetic friction between the object and surface, find the time at which the block comes to rest.
Solution:
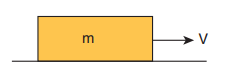
When the block slides, the force acting on the block is kinetic friction which is equal to f k = µk mg
From Newton’s second law ma = - µk mg
The negative sign implies that force acts on the opposite direction of motion.
The acceleration of the block while sliding a = - µk g.
The negative sign implies that the acceleration is in opposite direction of the velocity.
Note that the acceleration depends only on g and the coefficient of kinetic friction µk
We can apply the following kinematic equation
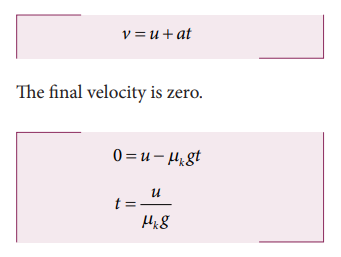
7. Three blocks of masses 10 kg, 7 kg and 2 kg are placed in contact with each other on a frictionless table. A force of 50 N is applied on the heaviest mass. What is the acceleration of the system?
Solution:
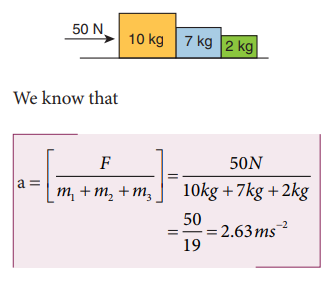
8. The coefficient of friction between a block and plane is 1/√3 If the inclination of the plane gradually increases, at what angle will the object begin to slide?
Since the coefficient of friction is 1/√3
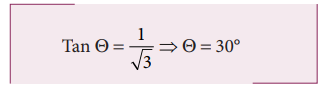
9. Find the maximum speed at which a car can turn round a curve of 36 m radius on a level road. Given the coefficient of friction between the tyre and the road is 0.53.
Radius of the curve r = 36 m
Coefficient of friction μ = 0.53
Acceleration due to gravity g = 10 ms-1
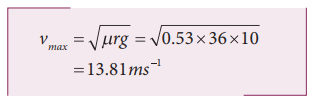
10. Calculate the centripetal acceleration of the Earth which orbits around the Sun. The Sun to Earth distance is appriximately 150 million km. (Assume the orbit of Earth to be circular)
The centripetal acceleration ac = v2/r
V - velocity of Earth around the orbit
r - radius of orbit or distance of Earth to Sun
Velocity of Earth is written in terms of angular velocity (ω) as

11. A block 1 of mass m1, constrained to move along a plane inclined at angle θ to the horizontal, is connected via a massless inextensible string that passes over a massless pulley, to a second block 2 of mass m2. Assume the coefficient of static friction between the block and the inclined plane is μs and the coefficient of kinetic friction is μk
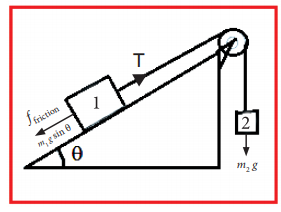
What is the relation between the masses of block 1 and block 2 such that the system just starts to slip?
Solution:
For all parts of this problem, it will be convenient to use different coordinate systems for the two different blocks. For block 1, take the positive x -direction to be up the incline, parallel to the plane, and the positive y -direction to be perpendicular to the plane, directed with a positive upward component. Take the positive direction of the position of block 2 to be downward.
The normal component N of the contact force between block 1 and the ramp will be
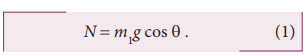
The net x -component of the force on block 1 is then
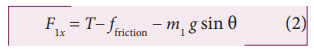
where T is the tension in the string
For the just-slipping condition, the frictional force has magnitude

The tension in the string is the gravitational force of the suspended mass,
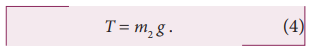
For the just-slipping condition, the net force on block 1 must be zero. Equations (2), (3) and (4) gives
0=m2g-μs m1g cos θ – m1g sin θ
m2=m1(μs cos θ + sin θ)
12. Consider two objects of masses 5 kg and 20 kg which are initially at rest. A force 100 N is applied on the two objects for 5 second.
a. What is the momentum gained by each object after 5 s.
b. What is the speed gained by each object after 5 s.
Final momentum on each object
∆P = F∆t = 100X 5 = 500 kgms−1
Final speed on the object of mass 5 kg = 500 /5 =100 m s–1
Final speed on the object of mass 20 kg =500/20 =μ25 m s–1
Note that momentum on each object is the same after 5 seconds but speed is not the same after 5 seconds. The heavier mass acquires lesser speed than the one with lower mass.
13. An object of mass 5 kg is initially at rest on the surface. The surface has coefficient kinetic friction µk = 0.6. What initial velocity must be given to the object so that it travels 10 m before coming to rest?
When the object moves on the surface it will experience three forces.
a) Downward gravitational force (mg)
b) Upward normal force (N)
c) Frictional force opposite to the motion of the object.
Since there is no motion along the vertical direction, magnitude of normal force is equivalent to the magnitude of gravitational force.
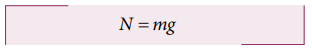
Applying Newton’s second law along the x direction
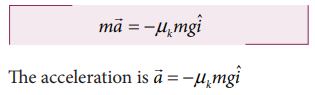
Note that the acceleration is along the x direction since the frictional force acts along the negative x direction.
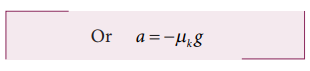
Note that the acceleration is uniform during the entire motion. We can use Newton’s kinematic equation to find the final velocity.

Here v = final velocity and u = initial velocity to be given to travel a distance s.
In this problem s = 10 m
Since the particle comes to rest, the final velocity v = 0

14. In the section 3.7.3 (Banking of road) we have not included the friction exerted by the road on the car. Suppose the coefficient of static friction between the car tyre and the surface of the road is , calculate the minimum speed with which the car can take safe turn?
When the car takes turn in the banked road, the following three forces act on the car.
(1) The gravitational force mg acting downwards
(2) The normal force N acting perpendicular to the surface of the road
(3) The static frictional force f acting on the car along the surface.
The following figure shows the forces acting on the horizontal and vertical direction.
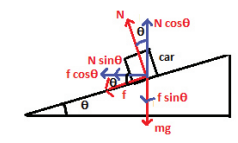
When the car takes turn with the speed v, the centripetal force is exerted by horizontal component of normal force and static frictional force. It is given by
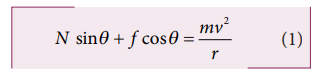
In the vertical direction, there is no acceleration. It implies that the vertical component of normal force is balanced by downward gravitational force and downward vertical component of frictional force. This can be expressed as
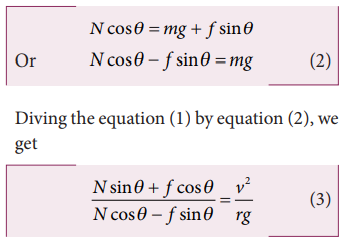
To calculate the maximum speed for the safe turn, we can use the maximum static friction is given by . By substituting this relation in equation (3), we get
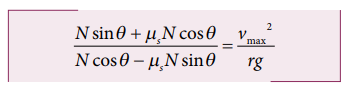
By taking outside the bracket in L.H.S of equation
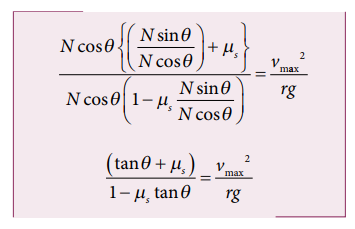
The Maximum speed for safe turn is given by
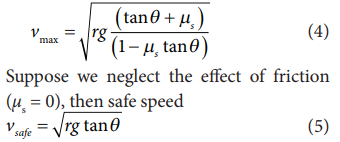
Note that the maximum speed with which the car takes safe turn is increased by friction (equation (4)). Suppose the car turns with speed v< vsafe , then the static friction acts up in the slope to prevent from inward skidding.
If the car turns with the speed little greater than, then the static friction acts down the slope to prevent outward skidding. But if the car turns with the speed greater than then static friction cannot prevent from outward skidding.
Solved Example Problems on Application of Newton’s Laws
Example 3.1
A book of mass m is at rest on the table.
1) What are the forces acting on the book?
2) What are the forces exerted by the book? (3) Draw the free body diagram for the book.
Solution
1) There are two forces acting on the book.
i. Gravitational force (mg) acting downwards on the book
ii. Normal contact force (N) exerted by the surface of the table on the book. It acts upwards as shown in the figure.
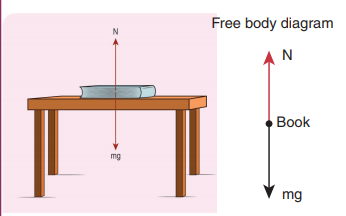
2) According to Newton’s third law, there are two reaction forces exerted by the book.
i. The book exerts an equal and opposite force (mg) on the Earth which acts upwards.
ii. The book exerts a force which is equal and opposite to normal force on the surface of the table (N) acting downwards.
3) The free body diagram of the book is shown in the figure.
Example 3.2
If two objects of masses 2.5 kg and 100 kg experience the same force 5 N, what is the acceleration experienced by each of them?
Solution
From Newton’s second law (in magnitude form), F = ma
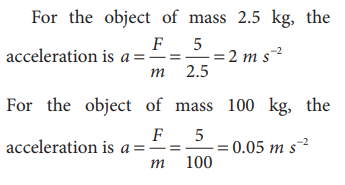
When an apple falls, it experiences Earth’s gravitational force. According to Newton’s third law, the apple exerts equal and opposite force on the Earth. Even though both the apple and Earth experience the same force, their acceleration is different. The mass of Earth is enormous compared to that of an apple. So an apple experiences larger acceleration and the Earth experiences almost negligible acceleration. Due to the negligible acceleration, Earth appears to be stationary when an apple falls.
Example 3.3
Which is the greatest force among the three force 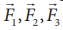 shown below
shown below
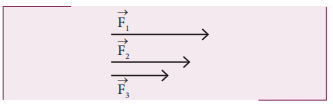
Solution
Force is a vector and magnitude of the vector is represented by the length of the vector. Here ![]() has greater length compared to other two. So
has greater length compared to other two. So ![]() is largest of the three.
is largest of the three.
Example 3.4
Apply Newton’s second law to a mango hanging from a tree. (Mass of the mango is 400 gm)
Solution
Note: Before applying Newton’s laws, the following steps have to be followed:
1. Choose a suitable inertial coordinate system to analyse the problem. For most of the cases we can take Earth as an inertial coordinate system.
2. Identify the system to which Newton’s laws need to be applied. The system can be a single object or more than one object.
3. Draw the free body diagram.
4. Once the forces acting on the system are identified, and the free body diagram is drawn, apply Newton’s second law. In the left hand side of the equation, write the forces acting on the system in vector notation and equate it to the right hand side of equation which is the product of mass and acceleration. Here, acceleration should also be in vector notation.
5. If acceleration is given, the force can be calculated. If the force is given, acceleration can be calculated.

By following the above steps:
We fix the inertial coordinate system on the ground as shown in the figure.
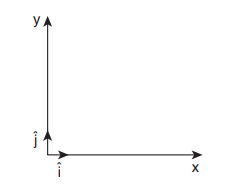
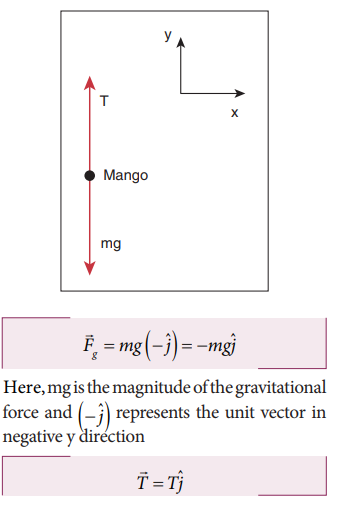
The forces acting on the mango are
i. Gravitational force exerted by the Earth on the mango acting downward along negative y axis
ii. Tension (in the cord attached to the mango) acts upward along positive y axis.
The free body diagram for the mango is shown in the figure

Example 3.5
A person rides a bike with a constant velocity ![]() with respect to ground and another biker accelerates with acceleration
with respect to ground and another biker accelerates with acceleration ![]() with respect to ground. Who can apply Newton’s second law with respect to a stationary observer on the ground?
with respect to ground. Who can apply Newton’s second law with respect to a stationary observer on the ground?
Solution
Second biker cannot apply Newton’s second law, because he is moving with acceleration ![]() with respect to Earth (he is not in inertial frame). But the first biker can apply Newton’s second law because he is moving at constant velocity with respect to Earth (he is in inertial frame).
with respect to Earth (he is not in inertial frame). But the first biker can apply Newton’s second law because he is moving at constant velocity with respect to Earth (he is in inertial frame).
Example 3.6
The position vector of a particle is given  which the particle experiences net force?
which the particle experiences net force?
Solution

Here, the particle has acceleration only along positive y direction. According to Newton’s second law, net force must also act along positive y direction. In addition, the particle has constant velocity in positive x direction and no velocity in z direction. Hence, there are no net force along x or z direction.
Example 3.7
Consider a bob attached to a string, hanging from a stand. It oscillates as shown in the figure.
Solution
a) Identify the forces that act on the bob?
b) b) What is the acceleration experienced by the bob?
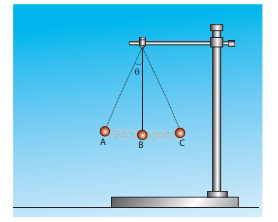
Two forces act on the bob.
(i) Gravitational force (mg) acting downwards
(ii) Tension (T) exerted by the string on the bob, whose position determines the direction of T as shown in figure.
The bob is moving in a circular arc as shown in the above figure. Hence it has centripetal acceleration. At a point A and C, the bob comes to rest momentarily and then its velocity increases when it moves towards point B. Hence, there is a tangential acceleration along the arc. The gravitational force can be resolved into two components (mg cosθ, mg sinθ) as shown below
Example 3.8
The velocity of a particle moving in a plane is given by the following diagram. Find out the direction of force acting on the particle?
Solution
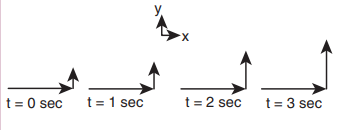
The velocity of the particle is 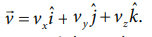 As shown in the figure, the particle is moving in the xy plane, there is no motion in the z direction. So velocity in the z direction is zero (vz = 0). The velocity of the particle has x component (vx) and y component (v y). From figure, as time increases from t = 0 sec to t = 3 sec, the length of the vector in y direction is changing (increasing). It means component of velocity ( vy ) is increasing with respect to time. According to Newton’s second law, if velocity changes with respect to time then there must be acceleration. In this case, the particle has acceleration in the y direction since the y component of velocity changes. So the particle experiences force in the y direction. The length of the vector in x direction does not change. It means that the particle has constant velocity in the x direction. So no force or zero net force acts in the x direction.
As shown in the figure, the particle is moving in the xy plane, there is no motion in the z direction. So velocity in the z direction is zero (vz = 0). The velocity of the particle has x component (vx) and y component (v y). From figure, as time increases from t = 0 sec to t = 3 sec, the length of the vector in y direction is changing (increasing). It means component of velocity ( vy ) is increasing with respect to time. According to Newton’s second law, if velocity changes with respect to time then there must be acceleration. In this case, the particle has acceleration in the y direction since the y component of velocity changes. So the particle experiences force in the y direction. The length of the vector in x direction does not change. It means that the particle has constant velocity in the x direction. So no force or zero net force acts in the x direction.
Example 3.9
Apply Newton’s second law for an object at rest on Earth and analyse the result.
Solution
The object is at rest with respect to Earth (inertial coordinate system). There are two forces that act on the object.
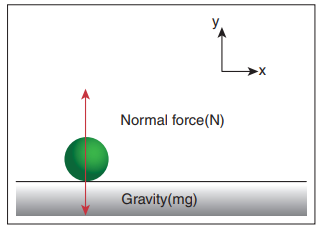
i. Gravity acting downward (negative y-direction)
ii. Normal force by the surface of the Earth acting upward (positive y-direction)
The free body diagram for this object is
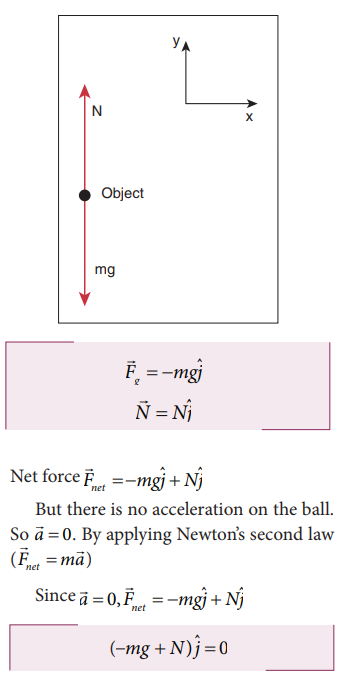
By comparing the components on both sides of the equation, we get
We can conclude that if the object is at rest, the magnitude of normal force is exactly equal to the magnitude of gravity.

Identify the forces acting on blocks A, B and C shown in the figure.
Solution

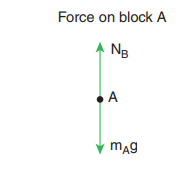
Forces on block A:
i. Downward gravitational force exerted by the Earth (mAg)
ii. Upward normal force (NB) exerted by block B (NB)
The free body diagram for block A is as shown in the following picture.
Forces on block B :
i. Downward gravitational force exerted by Earth (mBg)
ii. Downward force exerted by block A (NA)
iii. Upward normal force exerted by block C (NC)
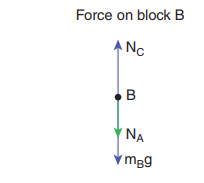
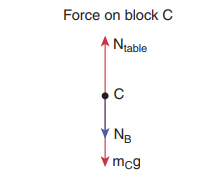
Forces onblock C:
i. Downward gravitational force exerted by Earth (mCg)
ii. Downward force exerted by block B (NB)
iii. Upward force exerted by the table (Ntable)
Example 3.12
Consider a horse attached to the cart which is initially at rest. If the horse starts walking forward, the cart also accelerates in the forward direction. If the horse pulls the cart with force Fh in forward direction, then according to Newton’s third law, the cart also pulls the horse by equivalent opposite force Fc = Fh in backward direction. Then total force on ‘cart+horse’ is zero. Why is it then the ‘cart+horse’ accelerates and moves forward?
Solution
This paradox arises due to wrong application of Newton’s second and third laws. Before applying Newton’s laws, we should decide ‘what is the system?’. Once we identify the ‘system’, then it is possible to identify all the forces acting on the system. We should not consider the force exerted by the system. If there is an unbalanced force acting on the system, then it should have acceleration in the direction of the resultant force. By following these steps we will analyse the horse and cart motion.
If we decide on the cart+horse as a ‘system’, then we should not consider the force exerted by the horse on the cart or the force exerted by cart on the horse. Both are internal forces acting on each other. According to Newton’s third law, total internal force acting on the system is zero and it cannot accelerate the system. The acceleration of the system is caused by some external force. In this case, the force exerted by the road on the system is the external force acting on the system. It is wrong to conclude that the total force acting on the system (cart+horse) is zero without including all the forces acting on the system. The road is pushing the horse and cart forward with acceleration. As there is an external force acting on the system, Newton’s second law has to be applied and not Newton’s third law.
The following figures illustrates this.
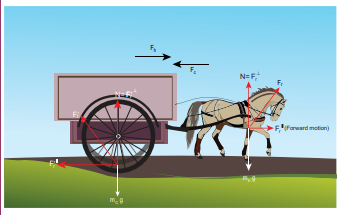
If we consider the horse as the ‘system’, then there are three forces acting on the horse.
i. Downward gravitational force (mh g )
ii. Force exerted by the road (Fr )
iii. Backward force exerted by the cart (Fc )
It is shown in the following figure.
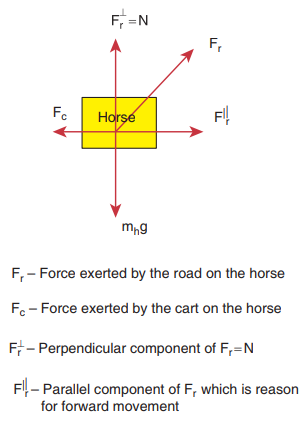
The force exerted by the road can be resolved into parallel and perpendicular components. The perpendicular component balances the downward gravitational force. There is parallel component along the forward direction. It is greater than the backward force (Fc ). So there is net force along the forward direction which causes the forward movement of the horse.
If we take the cart as the system, then there are three forces acting on the cart.
i. Downward gravitational force (mc g)
ii. Force exerted by the road ( Fr’ )
iii. Force exerted by the horse (Fh )
It is shown in the figure

The force exerted by the road ( ![]() ) can be resolved into parallel and perpendicular components. The perpendicular component cancels the downward gravity (mc g). Parallel component acts backwards and the force exerted by the horse (
) can be resolved into parallel and perpendicular components. The perpendicular component cancels the downward gravity (mc g). Parallel component acts backwards and the force exerted by the horse (![]() ) acts forward. Force (
) acts forward. Force (![]() ) is greater than the parallel component acting in the opposite direction. So there is an overall unbalanced force in the forward direction which causes the cart to accelerate forward.
) is greater than the parallel component acting in the opposite direction. So there is an overall unbalanced force in the forward direction which causes the cart to accelerate forward.
If we take the cart+horse as a system, then there are two forces acting on the system.
i. Downward gravitational force (mh + mc)g
ii. The force exerted by the road (Fr ) on the system.
It is shown in the following figure.
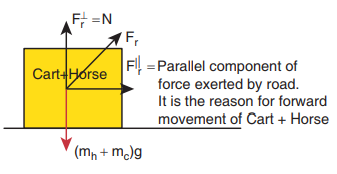
(iii) In this case the force exerted by the road (Fr ) on the system (cart+horse) is resolved in to parallel and perpendicular components. The perpendicular component is the normal force which cancels the downward gravitational force (mh + mc)g. The parallel component of the force is not balanced, hence the system (cart+horse) accelerates and moves forward due to this force.
Example 3.13
The position of the particle is represented by y = ut – 1/2 gt2 .
a) What is the force acting on the particle?
b) What is the momentum of the particle?
Solution
To find the force, we need to find the acceleration experienced by the particle.

The momentum of the particle = mv = m (u-gt).
The force acting on the object is given by F = ma = −mg
The negative sign implies that the force is acting on the negative y direction. This is exactly the force that acts on the object in projectile motion.
Solved Example Problems on Application of Lami’s Theorem
Example 3.14
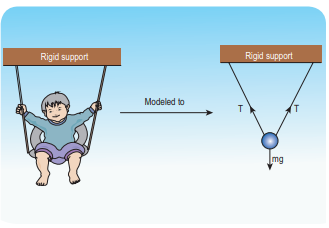
A baby is playing in a swing which is hanging with the help of two identical chains is at rest. Identify the forces acting on the baby. Apply Lami’s theorem and find out the tension acting on the chain.
Solution
The baby and the chains are modeled as a particle hung by two strings as shown in the figure. There are three forces acting on the baby.
i. Downward gravitational force along negative y direction (mg)
ii. Tension (T) along the two strings
These three forces are coplanar as well as concurrent as shown in the following figure.
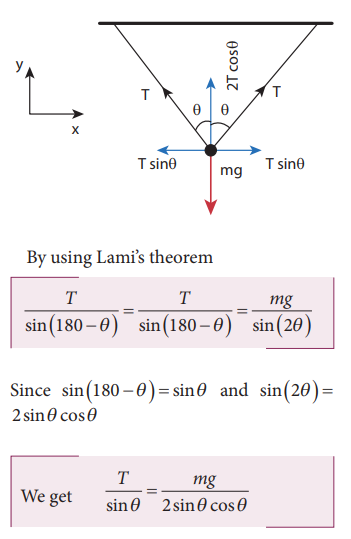
From this, the tension on each string is T = mg / 2cosθ
Solved Example Problems on Law of Conservation of Total Linear Momentum
Example 3.15
Identify the internal and external forces acting on the following systems.
a. Earth alone as a system
b. Earth and Sun as a system
c. Our body as a system while walking.
d. Our body + Earth as a system
Solution
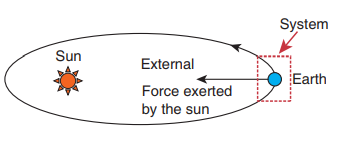
a. Earth alone as a system
Earth orbits the Sun due to gravitational attraction of the Sun. If we consider Earth as a system, then Sun’s gravitational force is an external force. If we take the Moon into account, it also exerts an external force on Earth.
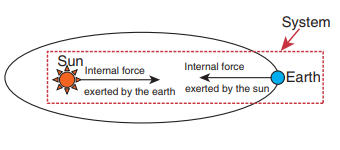
b. (Earth + Sun) as a system
In this case, there are two internal forces which form an action and reaction pair-the gravitational force exerted by the Sun on Earth and gravitational force exerted by the Earth on the Sun.
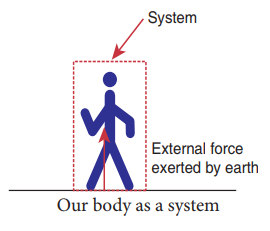
c. Our body as a system
While walking, we exert a force on the Earth and Earth exerts an equal and opposite force on our body. If our body alone is considered as a system, then the force exerted by the Earth on our body is external.
d. (Our body + Earth) as a system
In this case, there are two internal forces present in the system. One is the force exerted by our body on the Earth and the other is the equal and opposite force exerted by the Earth on our body.

Meaning of law of conservation of momentum
1. The Law of conservation of linear momentum is a vector law. It implies that both the magnitude and direction of total linear momentum are constant. In some cases, this total momentum can also be zero.
2. To analyse the motion of a particle, we can either use Newton’s second law or the law of conservation of linear momentum. Newton’s second law requires us to specify the forces involved in the process. This is difficult to specify in real situations. But conservation of linear momentum does not require any force involved in the process. It is covenient and hence important.
For example, when two particles collide, the forces exerted by these two particles on each other is difficult to specify. But it is easier to apply conservation of linear momentum during the collision process.
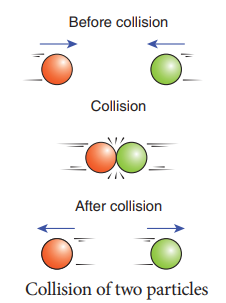
Examples
Consider the firing of a gun. Here the system is Gun+bullet. Initially the gun and bullet are at rest, hence the total linear momentum of the system is zero. Let ![]() be the momentum of the bullet and
be the momentum of the bullet and ![]() the momentum of the gun before firing. Since initially both are at rest,
the momentum of the gun before firing. Since initially both are at rest,

Consider two particles. One is at rest and the other moves towards the first particle (which is at rest). They collide and after collison move in some arbitrary directions. In this case, before collision, the total linear momentum of the system is equal to the initial linear momentum of the moving particle. According to conservation of momentum, the total linear momentum after collision also has to be in the forward direction. The following figure explains this.
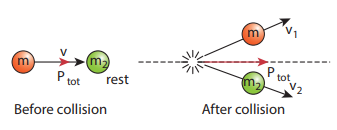
A more accurate calculation is covered in section 4.4. It is to be noted that the total momentum vector before and after collison points in the same direction. This simply means that the total linear momentum is constant before and after the collision. At the time of collision, each particle exerts a force on the other. As the two particles are considered as a system, these forces are only internal, and the total linear momentum cannot be altered by internal forces.
Solved Example Problems on Impulsive force or Impulse
Example 3.16
An object of mass 10 kg moving with a speed of 15 m s−1 hits the wall and comes to rest within
a. 0.03 second
b. 10 second
Calculate the impulse and average force acting on the object in both the cases.
Solution

We see that, impulse is the same in both cases, but the average force is different.
Solved Example Problems for Static Friction
Example 3.17
Consider an object of mass 2 kg resting on the floor. The coefficient of static friction between the object and the floor is µ s = 0.8. What force must be applied on the object to move it?
Solution
Since the object is at rest, the gravitational force experienced by an object is balanced by normal force exerted by floor.

Therefore to move the object the external force should be equal to maximum static friction.
Example 3.18
Consider an object of mass 50 kg at rest on the floor. A Force of 5 N is applied on the object but it does not move. What is the frictional force that acts on the object?
Solution
When the object is at rest, the external force and the static frictional force are equal and opposite.
The magnitudes of these two forces are equal, f s = Fext
Therefore, the static frictional force acting on the object is
Fs=5N
The direction of this frictional force is opposite to the direction of Fext .
Example 3.19
Two bodies of masses 7 kg and 5 kg are connected by a light string passing over a smooth pulley at the edge of the table as shown in the figure. The coefficient of static friction between the surfaces (body and table) is 0.9. Will the mass m1 = 7 kg on the surface move? If not what value of m2 should be used so that mass 7 kg begins to slide on the table?
Solution
As shown in the figure, there are four forces acting on the mass m1
a) Downward gravitational force along the negative y-axis (m1g)
b) Upward normal force along the positive y axis (N)
c) Tension force due to mass m2 along the positive x axis
d) Frictional force along the negative x axis
Since the mass m2 has no vertical motion, m1g = N
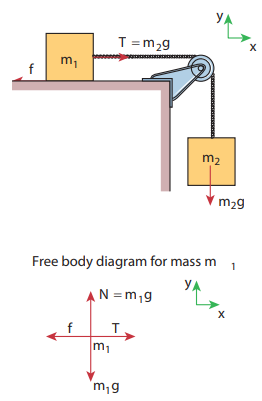
To determine whether the mass m1 moves on the surface, calculate the maximum static friction exerted by the table on the mass m1. If the tension on the mass m1 is equal to or greater than this maximum static friction, the object will move.
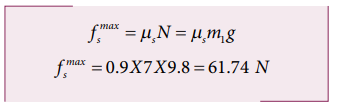
The tension T = m2 g = 5X9.8 = 49 N
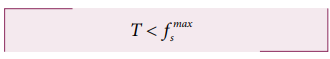
The tension acting on the mass m1 is less than the maximum static friction. So the mass m1 will not move.
To move the mass m1, T = fsmax where T = m2g

If the mass m2 is 6.3 kg then the mass m1 will begin to slide. Note that if there is no friction on the surface, the mass m1 will move for m2even for just 1 kg.
The values of coefficient of static friction for pairs of materials are presented in Table 3.1. Note that the ice and ice pair have very low coefficient of static friction. This means a block of ice can move easily over another block of ice.
Solved Example Problems for Angle of Repose
Example 3.20
A block of mass m slides down the plane inclined at an angle 60° with an acceleration g/2. Find the coefficient of kinetic friction?
Solution
Kinetic friction comes to play as the block is moving on the surface.
The forces acting on the mass are the normal force perpendicular to surface, downward gravitational force and kinetic friction fk along the surface.
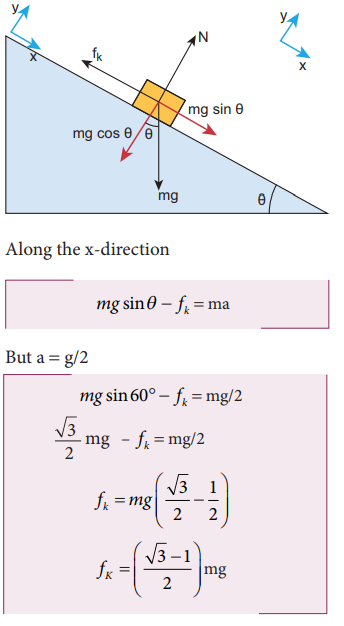
There is no motion along the y-direction as normal force is exactly balanced by the mg cosθ .
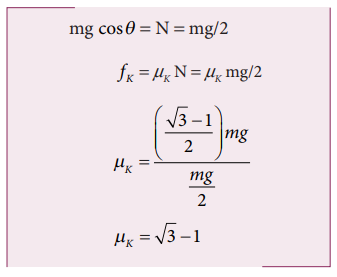
Solved Example Problems for Friction
Example 3.21
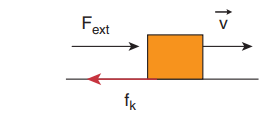
Consider an object moving on a horizontal surface with a constant velocity. Some external force is applied on the object to keep the object moving with a constant velocity. What is the net force acting on the object?
Solution
If an object moves with constant velocity, then it has no acceleration. According to Newton’s second law there is no net force acting on the object. The external force is balanced by the kinetic friction.
Solved Example Problems for Centripetal force
Example 3.22
If a stone of mass 0.25 kg tied to a string executes uniform circular motion with a speed of 2 m s-1 of radius 3 m, what is the magnitude of tensional force acting on the stone?
Solution
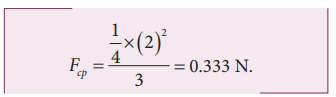
Example 3.23
The Moon orbits the Earth once in 27.3 days in an almost circular orbit. Calculate the centripetal acceleration experienced by the Earth? (Radius of the Earth is 6.4 × 106 m)
Solution
The centripetal acceleration is given by a = v2/r. This expression explicitly depends on Moon’s speed which is non trivial. We can work with the formula
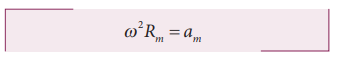
am is centripetal acceleration of the Moon due to Earth’s gravity.
ω is angular velocity.
Rm is the distance between Earth and the Moon, which is 60 times the radius of the Earth.

The centripetal acceleration of Moon towards the Earth is 0.00272 m s-2
Solved Example Problems for Vehicle on a leveled circular road
Example 3.24
Consider a circular leveled road of radius 10 m having coefficient of static friction 0.81. Three cars (A, B and C) are travelling with speed 7 ms-1, 8 m s-1 and 10 m s-1 respectively. Which car will skid when it moves in the circular level road? (g =10 m s-2)
Solution
From the safe turn condition the speed of the vehicle (v) must be less than or equal to
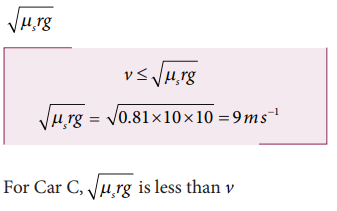
The speed of car A, B and C are 7 m s-1, 8 m s-1 and 10 m s-1 respectively. The cars A and B will have safe turns. But the car C has speed 10 m s-1 while it turns which exceeds the safe turning speed. Hence, the car C will skid.
Solved Example Problems for Banking of Tracks
Example 3.25
Consider a circular road of radius 20 meter banked at an angle of 15 degree. With what speed a car has to move on the turn so that it will have safe turn?
Solution
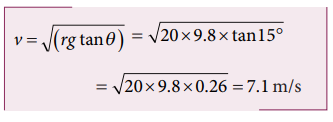
The safe speed for the car on this road is 7.1 m s-1
Solved Example Problems for Centrifugal Force due to Rotation of the Earth
Example 3.26
Calculate the centrifugal force experienced by a man of 60 kg standing at Chennai? (Given: Latitude of Chennai is 13°
Solution
The centrifugal force is given by Fc = mω2 R cosθ
The angular velocity (ω) of Earth = 2π/T.
where T is time period of the Earth (24 hours)

The radius of the Earth R = 6400 Km = 6400 × 103 m
Latitude of Chennai =13°
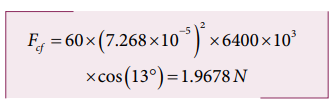
A 60 kg man experiences centrifugal force of approximately 2 Newton. But due to Earth’s gravity a man of 60 kg experiences a force =mg = 60 × 9.8 = 588N. This force is very much larger than the centrifugal force.
Related Topics