Book Back Numerical Problems

1. A force of 50N act on the object of mass 20 kg. shown in the figure. Calculate the acceleration of the object in x and y directions.

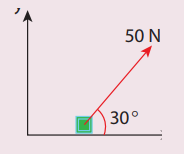
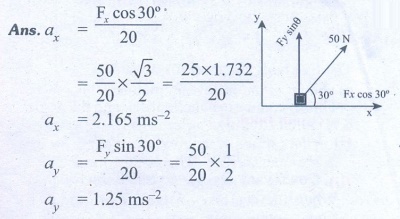
Ans: ax=2.165 ms-2; ay=1.25 ms-2

2. A spider of mass 50 g is hanging on a string of a cob web as shown in the figure. What is the tension in the string?

Answer:

T = mg

Mass (m)  = 50g = 0.050 kg

g = 9.8 ms-2

T = 0.050 × 9.8

= 0.49 N.

Ans: T=0.49N

3. What is the reading shown in spring balance?

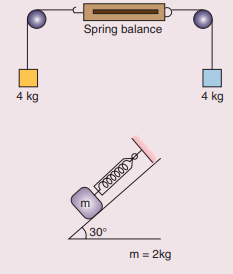
Answer:

Zero, 9.8 N. The weight of the body is equal to the acceleration due to gravity.

Ans: Zero, 9.8 N

4. The physics books are stacked on each other in the sequence: +1 volumes 1 and 2; +2 volumes 1 and 2 on a table.

a. Identify the forces acting on each book and draw the free body diagram.

b. Identify the forces exerted by each book on the other.

Answer:

(i) Gravitation force mg acting downwards on the books +1 vol. 1, vol. 2, +2. vol. 1, +2 vol. 2.

(ii) Upward normal force (NB) exerted by book B(NB).

(iii) Normal contact force (N) exerted by the vol. 2 on the book vol. 1 and so on.

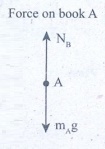
Forces on book A:

(i) Downward gravitational force exerted by the Earth (mAg)

(ii) Upward normal force (NB) exerted by book B (NB)

The free body diagram for book A is as shown in the following picture.

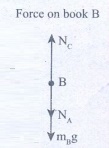
Force on book B

(i) Downward gravitational force exerted by Earth (mBg)

(ii) Downward force exerted by book A (NA)

(iii)Upward normal force exerted by book C (Nc)

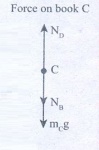
Forces oil book C:

(i) Downward gravitational force exerted by Earth (mcg)

(ii) Downward force exerted by book B(NB)

(iii) Upward normal force exerted by the book (ND)

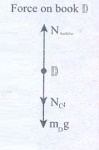
Forces on book D:

(i) Downward gravitational force exerted by Earth (mDg)

(ii) Downward force exerted by book C (Nc)

(iii) Upward force exerted by the table (Ntable)

5. A bob attached to the string oscillates back and forth. Resolve the forces acting on the bob in to components. What is the acceleration experience by the bob at an angle θ.

Answer:

(i) The radial force = T - mg cos θ provides centripetal force but no torque about support O.

(ii) The tangential force mg sin θ provide the restoring torque.

Tangential acceleration α = tangential force/ m

= g sin θ

Centripetal acceleration = T – mg cos θ / m

Ans: Tangential acceleration = g sinθ ; centripetal acceleration = (T−mg cosθ)/m

6. Two masses m1 and m2 are connected with a string passing over a frictionless pulley fixed at the corner of the table as shown in the figure. The coefficient of static friction of mass m1 with the table is μs. Calculate the minimum mass m3 that may be placed on m1to prevent it from sliding. Check if m1=15 kg, m2=10 kg, m3=25 and μs =0.2

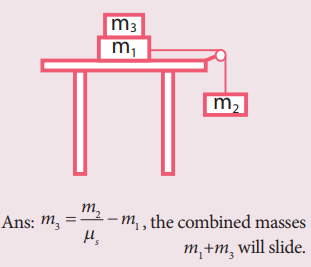
Answer:

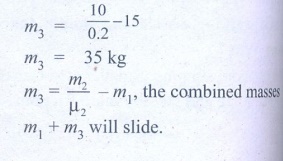
7. Calculate the acceleration of the bicycle of mass 25 kg as shown in Figures 1 and 2.

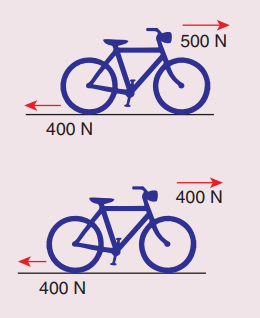
Answer

(i) Net force F1 = 500 - 400 = 100 N

Mass m = 25 kg; a = ?

Acceleration a = F/ m

a = 100/ 25 = 4 ms-2

(ii) Net force acting on cycle F2 = 400 - 400 = 0.

a = 0.

Ans: a=4 ms-2, zero

8. Apply Lami’s theorem on sling shot and calculate the tension in each string ?

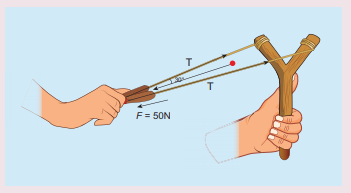
Answer:

Force F = mg = 50 N;

 θ  = 30 °

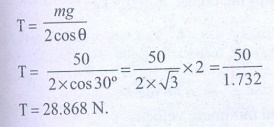
T= 28.868 N.

Ans: T= 28.868N.

9. A football player kicks a 0.8 kg ball and imparts it a velocity 12 ms-1. The contact between the foot and ball is only for one- sixtieth of a second. Find the average kicking force.

Answer:

Time of contact = 1/60 s

Mass of ball = 0.8 kg.

Velocity v = 12 ms-1

Average force = Δp/Δt

Favg = 0.8x12 / (1/60)

= 0.8 × 12 × 60 = 576 N .

Average kicking force = 576 N.

Ans: 576N.

10. A stone of mass 2 kg is attached to a string of length 1 meter. The string can withstand maximum tension 200 N. What is the maximum speed that stone can have during the whirling motion?

Answer:

Length, r = 1 m

Mass = 2 kg

Ans: vmax=10ms-1

11. Imagine that the gravitational force between Earth and Moon is provided by an invisible between the Moon and Earth. What is the tension that exists in this invisible string due to Earth’s centripetal force?

(Mass of the Moon = 7.34 × 1022  kg, Distance between Moon and Earth = 3.84 × 108 m)

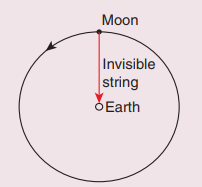
Answer

Tension T = Centripetal force

Centripetal force F = m × Centripetal acceleration

F = m × 0.00272

= 7.34 × 1022 × 0.00272 = 0.0199 × 1022

= 1.99 × 1020 = 2 × 1020N.

(i) The centripetal acceleration is given by a = v2/r. This expression explicitly depends on Moon’s speed which is non-trivial. We can work with the formula

ω2Rm = am

(ii) am is centripetal acceleration of the Moon due to Earth’s gravity,

ω is angular velocity.

(iii) Rm is the distance between Earth and the Moon, which is 60 times the radius of the Earth

Rm = 60R = 60 × 6.4 × 106 = 384 × 106 m.

(iv) As we know the angular velocity ω = 2π/T and T = 27.3 days = 27.3 × 24 × 60 × 60 second = 2.358 × 106 sec. By substituting these values in the formula for acceleration

am = (4π2)(384×106) / (2.358×106)2 = 0.00272 ms-2.

The centripetal acceleration of Moon towards the Earth is 0.00272 ms-2.

T ~ 2 × 1020N

Ans: T = 2 x 1020 N.

12. Two bodies of masses 15 kg and 10 kg are connected with light string kept on a smooth surface. A horizontal force F=500 N is applied to a 15 kg as shown in the figure. Calculate the tension acting in the string

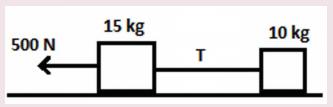
Answer:

Ans: T = 200N .

13. People often say “For every action there is an equivalent opposite reaction”. Here they meant ‘action of a human’. Is it correct to apply Newton’s third law to human actions? What is mean by ‘action’ in Newton third law? Give your arguments based on Newton’s laws.

Answer:

Newton’s third law is applicable to only human’s actions which involves physical force. Third law is not applicable to human’s psychological! actions or thoughts.

Ans: Newton’s third law is applicable to only human’s actions which involves physical force. Third law is not applicable to human’s psychological actions or thoughts

14. A car takes a turn with velocity 50 m s-1 on the circular road of radius of curvature 10 m. calculate the centrifugal force experienced by a person of mass 60kg inside the car?

Answer:

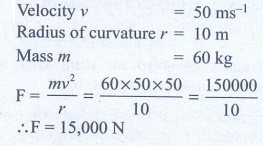
Ans: 15,000 N

15. A long stick rests on the surface. A person standing 10 m away from the stick. With what minimum speed an object of mass 0.5 kg should he thrown so that it hits the stick. (Assume the coefficient of kinetic friction is 0.7).

Ans: 11.71 m s-1