Chapter: 11th Physics : UNIT 3 : Laws of Motion
Angle of Repose
Angle of Repose
Consider an inclined plane on which an object is placed, as shown in Figure 3.30. Let the angle which this plane makes with the horizontal be θ . For small angles of θ , the object may not slide down. As θ is increased, for a particular value of θ , the object begins to slide down. This value is called angle of repose. Hence, the angle of repose is the angle of inclined plane with the horizontal such that an object placed on it begins to slide.
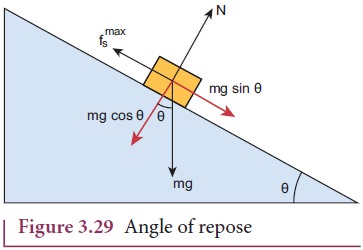
Let us consider the various forces in action here. The gravitational force mg is resolved into components parallel ( mg sinθ) and perpendicular (mg cosθ) to the inclined plane.
The component of force parallel to the inclined plane (mg sinθ) tries to move the object down.
The component of force perpendicular to the inclined plane (mg cosθ) is balanced by the Normal force (N).
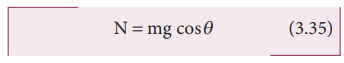
When the object just begins to move, the static friction attains its maximum value
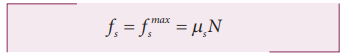
This friction also satisfies the relation
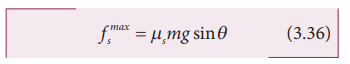
Equating the right hand side of equations (3.35) and (3.36), we get
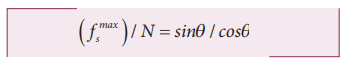
From the definition of angle of friction, we also know that
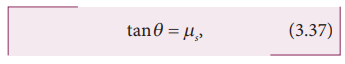
in which θ is the angle of friction.
Thus the angle of repose is the same as angle of friction. But the difference is that the angle of repose refers to inclined surfaces and the angle of friction is applicable to any type of surface.
Solved Example Problems for Angle of Repose
Example 3.20
A block of mass m slides down the plane inclined at an angle 60° with an acceleration g/2. Find the coefficient of kinetic friction?
Solution
Kinetic friction comes to play as the block is moving on the surface.
The forces acting on the mass are the normal force perpendicular to surface, downward gravitational force and kinetic friction fk along the surface.
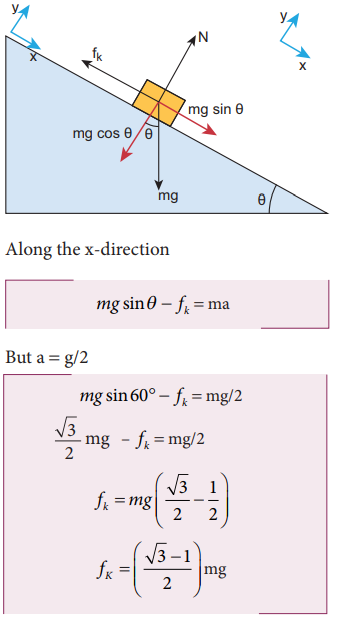
There is no motion along the y-direction as normal force is exactly balanced by the mg cosθ .
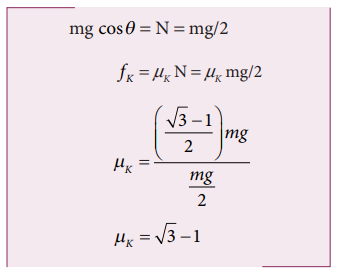
Related Topics