Application of Newton’s Laws: Two Bodies in Contact on a Horizontal Surface

Two Bodies in Contact on a Horizontal Surface

Consider two blocks of masses m1 and m2 (m1 > m2) kept in contact with each other on a smooth, horizontal frictionless surface as shown in Figure 3.14.

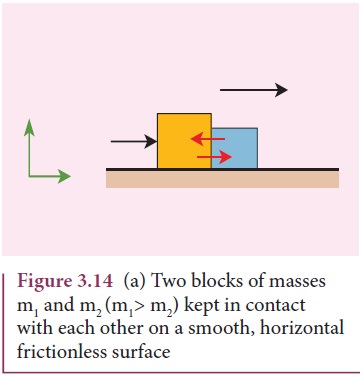
By the application of a horizontal force F, both the blocks are set into motion with acceleration ‘a’ simultaneously in the direction of the force F.

To find the acceleration  , Newton’s second law has to be applied to the system (combined mass m = m1 + m2)

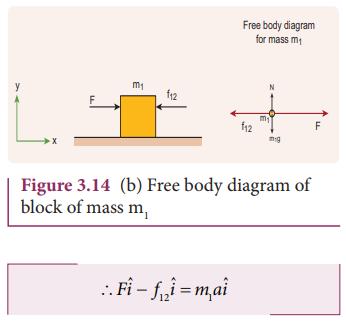
The force exerted by the block m1 on m2 due to its motion is called force of contact . According to Newton’s third law, the block m 2 will exert an equivalent opposite reaction force  on block m1.

Figure 3.14 (b) shows the free body diagram of block m1.

By comparing the components on both sides of the above equation, we get

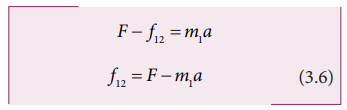
Substituting the value of acceleration from equation (3.5) in (3.6) we get

Equation (3.7) shows that the magnitude of contact force depends on mass m2 which provides the reaction force. Note that this force is acting along the negative x direction.

In vector notation, the reaction force on mass m1 is given by

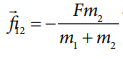
For mass m2 there is only one force acting on it in the x direction and it is denoted by  This force is exerted by mass m1. The free body diagram for mass m2 is shown in Figure 3.14 (c).

By comparing the components on both sides of the above equation

Applying Newton’s second law for mass m2

f21iˆ = m2aiˆ