with Answers, Solution | Atomic and Nuclear Physics | Physics - Example Solved Numerical Problems | 12th Physics : UNIT 9 : Atomic and Nuclear Physics
Chapter: 12th Physics : UNIT 9 : Atomic and Nuclear Physics
Example Solved Numerical Problems
Bohr atom model - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.1
The radius of the 5th orbit of hydrogen atom is 13.25 Å. Calculate the wavelength of the electron in the 5th orbit.
Solution:
2πr = nλ
2 × 3.14 × 13.25Å = 5 × λ
λ = 16.64Å
EXAMPLE 8.2
Find the (i) angular momentum (ii) velocity of the electron in the 5th orbit of hydrogen atom. (h = 6.6 × 10–34 Js, m = 9.1 × 10–31 kg)
Solution

EXAMPLE 8.3
(a) Show that the ratio of velocity of an electron in the first Bohr orbit to the speed of light c is a dimensionless number.
(b) Compute the velocity of electrons in ground state, first excited state and second excited state in Bohr atom model.
Solution
(a) The velocity of an electron in nth orbit is
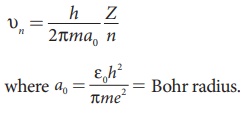
Substituting for a0 in υn,
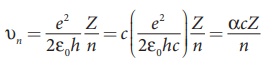
where c is the speed of light in free space or vacuum and its value is c = 3 × 108 m s–1and α is called fine structure constant.
For a hydrogen atom, Z = 1 and for the first orbit, n = 1, the ratio of velocity of electron in first orbit to the speed of light in vacuum or free space is
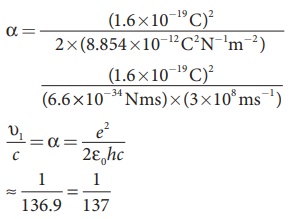
which is a dimensionless number
⇒ α = 1/137
(b) Using fine structure constant, the velocity of electron can be written as
υn = αcZ / n
For hydrogen atom (Z = 1) the velocity of electron in nth orbit is
υn = c/137 × 1/n = (2.19×106) × 1/n ms−1
For the first orbit (ground state), the velocity of electron is
υ = 2.19×106 ms−1
For the second orbit (first excited state), the velocity of electron is
υ2 = 1.095×106 ms−1
For the third orbit (second excited state), the velocity of electron is
υ3 = 0.73×106 ms−1
Here, υ1 > υ2 > υ3
EXAMPLE 8.4
The Bohr atom model is derived with the assumption that the nucleus of the atom is stationary and only electrons revolve around the nucleus. Suppose the nucleus is also in motion, then calculate the energy of this new system.
Solution
Let the mass of the electron be m and mass of the nucleus be M. Since there is no external force acting on the system, the centre of mass of hydrogen atom remains at rest. Hence, both nucleus and electron move about the centre of mass as shown in figure.
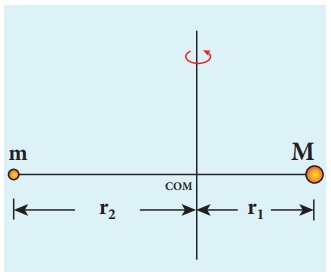
Let V be the velocity of the nuclear motion and υ be the velocity of electron motion. Since the total linear momentum of the system is zero,
−mυ + Mυ = 0 or
MV = mυ = p

Since the potential energy of the system is same, the total energy of the hydrogen can be expressed by replacing mass by reduced mass, which is
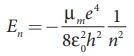
Since the nucleus is very heavy compared to the electron, the reduced mass is closer to the mass of the electron.
EXAMPLE 8.5
Suppose the energy of a hydrogen–like atom is given as En = − 54.4/n2 eV where n∈N . Calculate the following:
(a) Sketch the energy levels for this atom and compute its atomic number.
(b) If the atom is in ground state, compute its first excitation potential and also its ionization potential.
(c) When a photon with energy 42 eV and another photon with energy 56 eV are made to collide with this atom, does this atom absorb these photons?
(d) Determine the radius of its first Bohr orbit.
(e) Calculate the kinetic and potential energies in the ground state.
Solutions
(a) Given that
En =− 54.4/n2 eV
For n = 1, the ground state energy E1= –54.4 eV and for n = 2, E2 = –13.6 eV.
Similarly, E3 = –6.04 eV, E4 = –3.4 eV and so on.
For large value of principal quantum number – that is, n = ∞, we get E∞ = 0 eV.

(b) For a hydrogen-like atom, ground state energy is
E1 = − 13.6/n2 Z2 eV
where Z is the atomic number. Hence, comparing this energy with given energy, we get, – 13.6 Z2 = – 54.4 ⇒ Z = ±2. Since, atomic number cannot be negative number, Z = 2.
(c) The first excitation energy is
EI = E2 − E1 = −13.6eV −(−54.4 eV)
= 40.8eV
Hence, the first excitation potential is
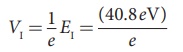
= 40.8 volt
The first ionization energy is
Eionization = E∞ − E1 = 0 −(−54.4 eV)
= 54.4 eV
Hence, the first ionization potential is
Vionization = 1/e Eionization = (54.4eV)/e
= 54.4 Volt
(d) Consider two photons to be A and B.
Given that photon A with energy 42 eV and photon B with energy 51 eV
From Bohr assumption, difference in energy levels is equal to photon energy, then atom will absorb energy, otherwise, not.
E2 − E1 = −13.6eV −(−54.4 eV)
= 40.8eV ≈ 41eV
Similarly,
E3 − E1 = −6.04 eV −(−54.4 eV)
= 48.36eV
E4 − E1 = −3.4 eV −(−54.4 eV)
= 51eV
E3 − E2 = −6.04 eV −(−13.6eV)
= 7.56eV
and so on.
But note that E2 – E1 ≠ 42 eV, E3 – E1 ≠ 42 eV, E4 – E1 ≠ 42 eV and E3 – E2 ≠ 42 eV.
For all possibilities, no difference in energy is an integer multiple of photon energy. Hence, photon A is not absorbed by this atom. But for Photon B, E4 – E1 = 51 eV, which means, Photon B can be absorbed by this atom.
(e) Since total energy is equal to negative of kinetic energy in Bohr atom model, we get
KEn = −En = −( − 54.4/n2 eV)
= 54.4/n2 eV
Potential energy is negative of twice the kinetic energy, which means,
Un = −2KEn = −2(54.4/n2 eV)
= −108.8/n2 eV
For a ground state, put n =1
Kinetic energy is KE1 = 54.4 eV and Potential energy is U1 = –108.8 eV
Atomic and nuclear masses - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.6
Calculate the average atomic mass of chlorine if no distinction is made between its different isotopes?
Solution
The element chlorine is a mixture of 75.77% of 3517Cl and 24.23% of 3717Cl . So the average atomic mass will be
(75.77/100) × 34.96885u + (24.23/100) × 36.96593u
= 35.453u
In fact, the chemist uses the average atomic mass or simply called chemical atomic weight (35.453 u for chlorine) of an element. So it must be remembered that the atomic mass which is mentioned in the periodic table is basically averaged atomic mass.
Size and density of the nucleus - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.7
Calculate the radius of 19779Au nucleus.
Solution
According to the equation (8.19),
R = 1.2 × 10-15 × (197)1/3 = 6.97 × 10-15m
Or R = 6.97 F
EXAMPLE 8.8
Calculate the density of the nucleus with mass number A.
Solution
From equation (8.19), the radius of the nuclei satisfy the equation = R0A1/3. Then the volume of the nucleus
V = 4/3 πR3 = 4/3 πR3A
By ignoring the mass difference between the proton and neutron, the total mass of the nucleus having mass number A is equal to A.m where m is mass of the proton and is equal to 1.6726 x 10-27 kg.
Mass defect and binding energy - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.9
Compute the binding energy of 42He nucleus using the following data: Atomic mass of Helium atom, MA (He) = 4.00260 u and that of hydrogen atom, mH = 1.00785u.
Solution:
Binding energy BE = [ZmH + Nmn - M A ]c2
For helium nucleus, Z = 2, N = A–Z = 4–2 = 2
Mass defect
∆m = [(2×1.00785u) + (2 ×1.008665u) - 4.00260 u] ∆m = 0.03038u
B.E = 0.03038u × c2
B.E = 0.03038 × 931MeV = 28 MeV
[1uc2 = 931MeV ]
The binding energy of the 42He nucleus is 28 MeV.
Binding energy curve - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.10
Compute the binding energy per nucleon of 42He nucleus.
Solution
From example 8.9, we found that the ![]() of 42He =28 Mev
of 42He =28 Mev
Binding energy per nucleon = ![]() = 28 MeV/4 = 7 MeV.
= 28 MeV/4 = 7 MeV.
Radioactivity: Alpha decay - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.11
(a) Calculate the disintegration energy when stationary 23292U nucleus decays to thorium 22890Th with the emission of α particle. The atomic masses are of 23292U = 232.037156 u , 22890Th = 228.028741u and 42He = 4.002603u
(b) Calculate kinetic energies of 22890Th and α-particle and their ratio.
Solution
The difference in masses
∆m = (mU – mTh - mα)
= (232.037156–228.028741 – 4.002603)u
The mass lost in this decay = 0.005812 u
Since 1u = 931MeV, the energy Q released is
Q = (0.005812u)×(931MeV / u)
= 5.41MeV
This disintegration energy Q appears as the kinetic energy of α particle and the daughter nucleus.
In any decay, the total linear momentum must be conserved.
Total linear momentum of the parent nucleus = total linear momentum of the daughter nucleus +α particle
Since before decay, the uranium nucleus is at rest, its momentum is zero.
By applying conservation of momentum, we get
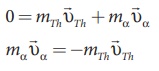
It implies that the alpha particle and daughter nucleus move in opposite directions.
In magnitude mα υα = mThυTh
The velocity α particle υα = [mTh/mα] υTh.
Note that mTh /ma > 1, so υα > υTh . The ratio of the kinetic energy of α particle to the daughter nucleus
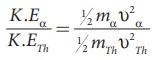
By substituting, the value of υα into the above equation, we get
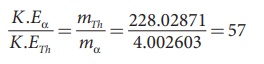
The kinetic energy of α particle is 57 times greater than the kinetic energy of the daughter nucleus (22890Th ).
The disintegration energy Q = total kinetic energy of products
K.Eα + K.ETh = 5.41MeV
57K.ETh + K.ETh = 5.41MeV
K.ETh = 5.41/58 MeV = 0.093MeV
K.Eα = 57K.ETh = 57×0.093 = 5.301MeV
In fact, 98% of total kinetic energy is taken by the α particle.
Half-life - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.12
Calculate the number of nuclei of carbon-14 undecayed after 22,920 years if the initial number of carbon-14 atoms is 10,000. The half-life of carbon-14 is 5730 years.
Solution
To get the time interval in terms of half- life,

The number of nuclei remaining undecayed after 22,920 years,
N = ( ½ )0 N0 = (1/2)4 ×10, 000
N = 625
EXAMPLE 8.13
A radioactive sample has 2.6 μg of pure 137N which has a half-life of 10 minutes (a) How many nuclei are present initially? (b) What is the activity initially? (c) What is the activity after 2 hours? (d) Calculate mean life of this sample.
Solution
(a) To find N0, we have to find the number of 137N atoms in 2.6μg . The atomic mass of nitrogen is 13. Therefore, 13 g of 137N contains Avogadro number ( 6.02 ×1023 ) of atoms.
In 1 g, the number of 137N is equal to be 6.02×1023 / 13 atoms. So the number of 137N atoms in 2.6μg is
N = (6.02×1023/13) × 2.6×10−6 = 12.04×1016 atoms
(b) To find the initial activity R0, we have to evaluate decay constant λ
λ = 0.6931 / T1/2 = 0.6931 / 10×60 = 1.155×10−3 s−1
Therefore
R0 = λN0 = 1.155×10-3 ×12.04×1016
=13.90×1013 decays/s
= 13.90×1013 Bq
In terms of a curie,
R0 = 13.90×1015 / 3.7×1010 = 3.75×103 Ci
since 1Ci = 3.7×1010Bq
(c) Activity after 2 hours can be calculated in two different ways:
Method 1: R = R0e–λt
At t = 2 hr = 7200 s
R = 3.75 × 103 × e–7200 ×1.155 ×10–3
R = 3.75 × 103 × 2.4 ×10–4 = 0.9 Ci
Method 2: R = (1/2)n R0
Here n = 120 min /10 min = 12
R = (1/2)12 ×3.75×103 ≈ 0.9Ci
(d) mean life τ = T1/2 / 0.6931 = 10×60 / 0.6931
= 865.67 s
Carbon dating - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.14
Keezhadi (கீழடி), a small hamlet, has become one of the very important archeological places of Tamilandu. It is located in Sivagangai district. A lot of tools, jewellery and charcoal, etc.) have been unearthed in Keezhadi which have given substantial evidence that an ancient urban civilization had thrived on the banks of river Vaigai. To determine the age of those materials, the charcoal of 200 g sent for carbon dating is given in the following figure (b). The activity of 146C is found to be 38 decays/s. Calculate the age of charcoal.

Solution
To calculate the age, we need to know the initial activity (R0) of the characol (when the sample was alive).
The activity R of the sample
R = R0 e−λt (1)
To find the time t, rewriting the above equation (1), eλt = R0/R
By taking the logarithm on both sides, we get

Here R = 38 decays/s=38 Bq.
To find decay constant, we use the equation
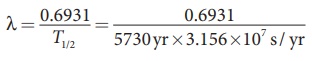
[∴ 1yr = 365.25 × 24 × 60 × 60 s = 3.156 × 107 s]
λ = 3.83×10−12 s−1
To find the initial activity R0, we use the equation R0 = λN0 . Here N0 is the number of carbon-14 atoms present in the sample when it was alive. The mass of the characol is 200 g. In 12 g of carbon, there are 6.02 ×1023 carbon atoms. So 200 g contains,
[{ 6.02×1023 atoms / mol } / {12g / mol } ] × 200 ≈ 1×1025 Atoms
When the tree(sample) was alive, the ratio of 146C to 126C is 1.3 ×10-12 . So the total number of carbon-14 atoms is given by
N0 = 1×1025×1.3×10−12 = 1.3×1013 atoms
The initial activity
R0 = 3.83×10−12 ×1.3×1013 ≈ 50 decays / s
= 50 Bq
By substituting the value of R0 and λ in the equation (2), we get

In fact, the excavated materials were sent for carbon dating to USA by Archeological Department of Tamilnadu and the report confirmed that the age of Keezhadi artefacts lies between 2200 years to 2500 years (Sangam era- 400 BC to 200 BC). The Keezhadi excavations experimentally proved that urban civilization existed in Tamil Nadu even 2000 years ago!
Nuclear Fission - Numerical Problems Questions with Answers, Solution
EXAMPLE 8.15
Calculate the amount of energy released when 1 kg of 93592U undergoes fission reaction.
Solution
235 g of 93592U has 6.02 ×1023 atoms. In one gram of 93592U , the number of atoms is equal to 6.02 ×1023 /235 = 2.56 ×1021 .
So the number of atoms in 1 kg of 93592U = 2.56 ×1021 ×1000 = 2.56 ×1024.
Each 93592U nucleus releases 200 MeV of energy during the fission. The total energy released by 1kg of 93592U is
Q = 2.56 ×1024 × 200MeV = 5.12 ×1026 MeV
By converting in terms of joules,
Q = 5.12 ×1026 ×1.6 ×10-13 J = 8.192 ×1013 J .
In terms of Kilowatt hour,
Q = 8.192 ×1013 / 3.6 ×106 = 2.27 ×107 kWh
This is enormously large energy which is enough to keep 100 W light bulb operating for 30,000 years. To produce this much energy through chemical reaction, around 20,000 tons of TNT(tri nitro toluene) has to be exploded.
Atomic and Nuclear Physics
Exercises
1. Consider two hydrogen atoms HA and HB in ground state. Assume that hydrogen atom HA is at rest and hydrogen atom HB is moving with a speed and make head-on collide on the stationary hydrogen atom HA. After the strike, both of them move together. What is minimum value of the kinetic energy of the moving hydrogen atom HB, such that any one of the hydrogen atoms reaches one of the excitation state.
[Ans: 20.4 eV]
Solution:

2. In the Bohr atom model, the frequency of transitions is given by the following expression
v = Rc ( 1/n2 – 1/m2 ) , where n < m,
Consider the following transitions:
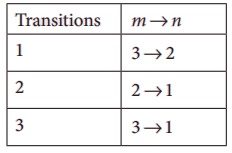
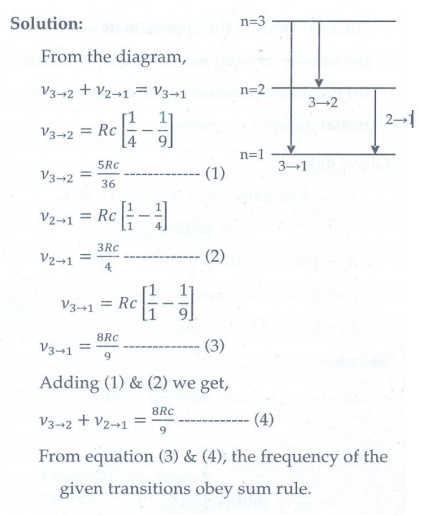
Show that the frequency of these transitions obey sum rule (which is known as Ritz combination principle)
[Ans: v3→2 + v2→1 = v3→1]
3. (a) A hydrogen atom is excited by radiation of wavelength 97.5 nm. Find the principal quantum number of the excited state.
(b) Show that the total number of lines in emission spectrum is n(n-1) / 2 and compute the total number of possible lines in emission spectrum.
[Ans: (a) n = 4 (b) 6 possible transitions]

4. Calculate the radius of the earth if the density of the earth is equal to the density of the nucleus.[mass of earth 5.97 × 1024 kg ].
[Ans:180m]
Given data:
Mass of the earth = 5.97 x 1024 kg
Density of earth = Density of nucleus
= 2.3 x 1017 kg m-3
Solution:
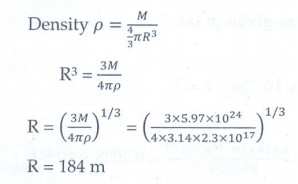
5. Calculate the mass defect and the binding energy per nucleon of the 10847Ag nucleus. [atomic mass of Ag = 107.905949]
Ans: [∆m = 0.990391u and B.E = 8.5MeV / A ]

Given data:
M = 107.905949 u
Z = 47 mH = 1.007825u
N = 61 mn =1.008665 u
Solution:

6. Half lives of two radioactive elements A and B are 20 minutes and 40 minutes respectively. Initially, the samples have equal number of nuclei. Calculate the ratio of decayed numbers of A and B nuclei after 80 minutes.
[Ans: 5:4]
Given data:
T1/2 of A = 20 min
T1/2 of B = 40 min ; Total time = 80 min
NOA = NOB
NOA - NA / NOB - NB = ?
Solutions:
Decayed number of nuclei = No – N

The ratio of decayed numbers of A and B is 5 : 4.
7. On your birthday, you measure the activity of the sample 210Bi which has a half-life of 5.01 days. The initial activity that you measure is 1μCi . (a) What is the approximate activity of the sample on your next birthday? Calculate (b) the decay constant (c) the mean life (d) initial number of atoms.
[Ans: (a) 10-22 μCi (b) 1.6 ×10-6 s-1 (c) 7.24days (d) 2.31×1010 ]
Given data:
T1/2 = 5.01 days = 5.01 × 24 × 60 × 60 s
= 4.328 × 105 s
R0 = 1 μCi = 1 × 10-6 × 3.7 × 1010 Bq
t = 1 year = 365 days
Rt = ? ; λ=?; τ = ? ; N0 = ?
Solution:

8. Calculate the time required for 60% of a sample of radon undergo decay. Given T1/2 of radon =3.8 days
[Ans: 5.022 days]
Given data:
T1/2 = 3.8 days; λ= 0.693/3.8 per day
Amount of sample decayed = 60% of No
Amount of sample present (N) = 40% of No
No is initial amount of sample, t = ?
Solution:
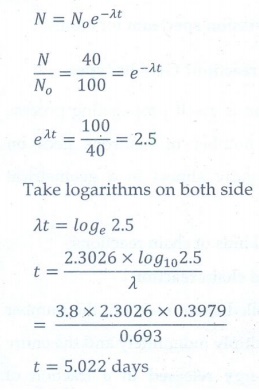
9. Assuming that energy released by the fission of a single 23592U nucleus is 200MeV, calculate the number of fissions per second required to produce 1 watt power.
[Ans: 3.125 ×1010 ]
Given data:
Energy released during fission of single
23492U = 200MeV
Power = 1 watt = 1 J/s
No. of fissions per second required to produce
1W power = ?
Solution:
Energy produced = no. of fissions per second × energy released per fission
No.of fissions per second = energy produced / energy released per fission
= 1 / ( 200 ×106 ×1.6 ×10-19)
= 1/ (320 × 10-13)
= 1013/320 = 3.125 ×1010
No. of fissions per second = 3.125 × 1010
10. Show that the mass of radium ( 22688Ra ) with an activity of 1 curie is almost a gram. Given T1/2 =1600 years.
Given: T1/2 =1600 years (PTA-6)
Given data:
Ro = 1Ci= 3.7 × 1010 Bq
T1/2 = 1600 years
Mass of radium with an activity of 1 Ci= ?
Solution:

∴ The mass of radium with an activity of 1 Ci is almost a gram.
11. Characol pieces of tree is found from an archeological site. The carbon-14 content of this characol is only 17.5% that of equivalent sample of carbon from a living tree. What is the age of tree?
[Ans: 1.44 × 104 yr]
Given data:
The amount of 14C present (N) = 17.5% of No
T1/2 = 5730 years
Age of the tree (t) = ?
Solution:
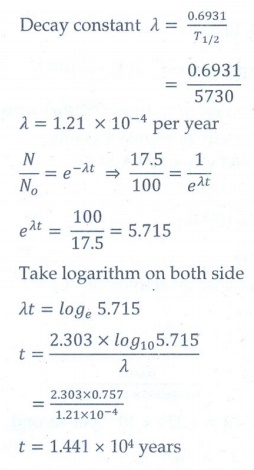
Related Topics