Carbon dating

Carbon dating

The interesting application of beta decay is radioactive dating or carbon dating. Using this technique, the age of an ancient object can be calculated. All living organisms absorb carbon dioxide (CO₂) from air to synthesize organic molecules. In this absorbed CO₂, the major part is ¹²₆C and very small fraction (1.3 ×10^-12 ) is radioactive ¹⁴₆C whose half-life is 5730 years.

Carbon-14 in the atmosphere is always decaying but at the same time, cosmic rays from outer space are continuously bombarding the atoms in the atmosphere which produces ¹⁴₆C . So the continuous production and decay of ¹⁴₆C in the atmosphere keep the ratio of ¹⁴₆C to ¹²₆C always constant. Since our human body, tree or any living organism continuously absorb CO₂ from the atmosphere, the ratio of ¹⁴₆C to ¹²₆C in the living organism is also nearly constant. But when the organism dies, it stops absorbing CO₂. Since ¹⁴₆C starts to decay, the ratio of ¹⁴₆C to ₆¹²C in a dead organism or specimen decreases over the years. Suppose the ratio of ¹⁴₆C to ¹²₆C in the ancient tree pieces excavated is known, then the age of the tree pieces can be calculated.

EXAMPLE 8.14

Keezhadi (கீழடி), a small hamlet, has become one of the very important archeological places of Tamilandu. It is located in Sivagangai district. A lot of tools, jewellery and charcoal, etc.) have been unearthed in Keezhadi which have given substantial evidence that an ancient urban civilization had thrived on the banks of river Vaigai. To determine the age of those materials, the charcoal of 200 g sent for carbon dating is given in the following figure (b). The activity of ¹⁴₆C is found to be 38 decays/s. Calculate the age of charcoal.

Solution

To calculate the age, we need to know the initial activity (R₀) of the characol (when the sample was alive).

The activity R of the sample

R = R₀ e^−λt       (1)

To find the time t, rewriting the above equation (1), e^λt = R₀/R

By taking the logarithm on both sides, we get

Here R = 38 decays/s=38 Bq.

To find decay constant, we use the equation

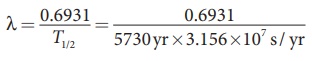
[∴ 1yr = 365.25 × 24 × 60 × 60 s = 3.156 × 10⁷ s]

λ = 3.83×10^−12 s^−1

To find the initial activity R₀, we use the equation R₀ = λN₀ . Here N₀ is the number of carbon-14 atoms present in the sample when it was alive. The mass of the characol is 200 g. In 12 g of carbon, there are 6.02 ×10²³ carbon atoms. So 200 g contains,

[{ 6.02×10²³ atoms / mol } / {12g / mol } ] × 200 ≈ 1×10²⁵ Atoms

When the tree(sample) was alive, the ratio of ¹⁴₆C to ¹²₆C is 1.3 ×10^-12 . So the total number of carbon-14 atoms is given by

N₀ = 1×10²⁵×1.3×10^−12 = 1.3×10¹³ atoms

The initial activity

R₀ = 3.83×10^−12 ×1.3×10¹³ ≈ 50 decays / s

= 50 Bq

By substituting the value of R₀ and λ in the equation (2), we get

In fact, the excavated materials were sent for carbon dating to USA by Archeological Department of Tamilnadu and the report confirmed that the age of Keezhadi artefacts lies between 2200 years to 2500 years (Sangam era- 400 BC to 200 BC). The Keezhadi excavations experimentally proved that urban civilization existed in Tamil Nadu even 2000 years ago!