Mass defect and binding energy

Mass defect and binding energy

It is experimentally found out that the mass of any nucleus is always less than the sum of the mass of its individual constituents. For example, consider the carbon-12 nucleus which is made up of 6 protons and 6 neutrons.

Mass of 6 neutrons = 6×1.00866 u = 6.05196u

Mass of 6 protons = 6 ×1.00727 u = 6.04362 u

Mass of 6 electrons = 6 × 0.00055u = 0.0033u

The expected mass of carbon-12 nucleus

= 6.05196 u + 6.04362 u = 12.09558u

But using mass spectroscopy, the atomic mass of carbon-12 atom is found to be 12 u. So if we subtract the mass of 6 electrons (0.0033 u) from 12 u, we get the carbon-12 nuclear mass which is equal to 11.9967 u. Note that the experimental mass of carbon-12 nucleus is less than the total mass of its individual constituents by ∆m = 0.09888u . This difference in mass ∆m is called mass defect. In general, if M, m_p and m_n are mass of the nucleus ( ^A_zX ), the mass of a proton and the mass of a neutron respectively, then the mass defect is given by

∆m = (Zm_p + Nm_n) - M             (8.20)

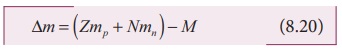
Where has this mass disappeared? The answer was provided by Albert Einstein with the help of famous mass-energy relation (E = mc² ) . According to this relation, the mass can be converted into energy and energy can be converted into mass. In the case of the carbon-12 nucleus, when 6 protons and 6 neutrons combine to form carbon-12 nucleus, mass equal to mass defect disappears and the corresponding energy is released. This is called the binding energy of the nucleus (BE) and is equal to (∆m)c² . In fact, to separate the carbon-12 nucleus into individual constituents, we must supply the energy equal to binding energy of the nucleus.

We can write the equation (8.20) in terms of binding energy

BE = (Zm_p + Nm_n + M )c²      (8.21)

It is always convenient to work with the mass of the atom than the mass of the nucleus. Hence by adding and subtracting the mass of the Z electrons, we get

BE = (Zm_p + Zm_e + Nm_n - M - Zm_e )c²           (8.22)

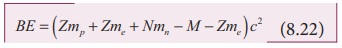
BE = [Z (m_p + m_e ) + Nm_n - M - Zm_e ] c²

where m_p + m_e = m_H (mass of hydrogen atom)

BE = [Zm_H + Nm_n - (M + Zm_e) c²       (8.23)

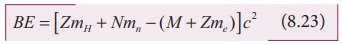
 Here M + Zm_e = M_A where M_A is the mass of the atom of an element ^A_ZX .

Finally, the binding energy in terms of the atomic masses is given by

BE = [Zm_H + Nm_n - M_A ] c²          (8.24)

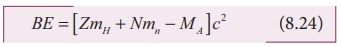
Using Einstein’s mass-energy equivalence, the energy equivalent of one atomic mass unit 1u = 1.66 ×10^-27 × (3 ×10⁸)²

 = 14.94 ×10^-11 J

≈ 931MeV

EXAMPLE 8.9

Compute the binding energy of ⁴₂He nucleus using the following data: Atomic mass of Helium atom, M_A (He) = 4.00260 u and that of hydrogen atom, m_H = 1.00785u.

Solution:

Binding energy BE = [Zm_H + Nm_n - M _A ]c²

For helium nucleus, Z = 2, N = A–Z = 4–2 = 2

Mass defect

∆m = [(2×1.00785u) + (2 ×1.008665u) - 4.00260 u] ∆m = 0.03038u

B.E = 0.03038u × c²

B.E = 0.03038 × 931MeV = 28 MeV

[1uc² = 931MeV ]

The binding energy of the  ⁴₂He nucleus is 28 MeV.