Law of radioactive decay

Law of radioactive decay

In the previous section, the decay process of a single radioactive nucleus was discussed. In practice, we have bulk material of radioactive sample which contains a vast number of the radioactive nuclei and not all the radioactive nucleus in a sample decay at the same time. It decays over a period of time and this decay is basically a random process. It implies that we cannot predict which nucleus is going to decay or rather we can determine like probabilistic basis (like tossing a coin). We can calculate approximately how many nuclei in a sample are decayed over a period of time.

At any instant t, the number of decays per unit time, called rate of decay (dN/dt) is proportional to the number of nuclei ( N ) at the same instant.

 dN/dt ∝ N

By introducing a proportionality constant, the relation can be written as

Here proportionality constant λ is called decay constant which is different for different radioactive sample and the negative sign in the equation implies that the N is decreasing with time.

By rewriting the equation (8.32), we get

dN = −λNdt       (8.33)

Here dN represents the number of nuclei decaying in the time interval dt.

Let us assume that at time t = 0 s, the number of nuclei present in the radioactive sample is N₀. By integrating the equation (8.33), we can calculate the number of undecayed nuclei N at any time t.

From equation (8.33), we get

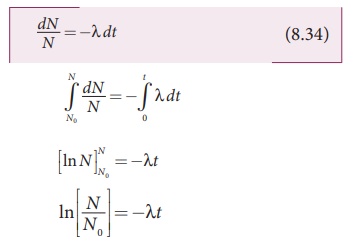
Taking exponentials on both sides, we get

N = N₀e^-λt  (8.35)

[Note: e^lnx = e^y ⇒ x = e ^y ]

Equation (8.35) is called the law of radioactive decay. Here N denotes the number of undecayed nuclei present at any time t and N₀ denotes the number of nuclei at initial time t=0. Note that the number of atoms is decreasing exponentially over the time. This implies that the time taken for all the radioactive nuclei to decay will be infinite. Equation (8.35) is plotted in Figure 8.26.

We can also define another useful quantity called activity (R) or decay rate which is the number of nuclei decayed per second and it is denoted as R = |dN/dt|. Note that activity R is a positive quantity.

From equation (8.35), we get

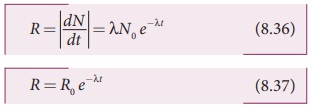
where R₀ = λN₀

The equation (8.37) is also equivalent to radioactive law of decay. Here R₀ is the activity of the sample at t=0 and R is the activity of the sample at any time t. From equation (8.37), activity also shows exponential decay behavior. The activity R also can be expressed in terms of number of undecayed atoms present at any time t.

From equation (8.37), since N = N₀e^−λt , we write

R = λN              (8.38)

Equation (8.35) implies that the activity at any time t is equal to the product of decay constant and number of undecayed nuclei at the same time t. Since N decreases over time, R also decreases.

The SI unit of activity R is Becquerel and one Becquerel (Bq) is equal to one decay per second. There is also another standard unit for the activity called Curie(Ci).

1 Curie =1 Ci = 3.7 ×10¹⁰ decays per second

1 Ci = 3.7 ×10¹⁰ Bq

Initially one curie was defined as number of decays per second in 1 g of radium and it is equal to 3.7 ×10¹⁰ decays/s.