Bohr atom model

ATOM MODEL

Bohr atom model

In order to overcome the limitations of the Rutherford atom model in explaining the stability and also the line spectrum observed for a hydrogen atom (Figure 8.14), Niels Bohr made modifications of Rutherford atom model. He is the first person to give better theoretical model of the structure of an atom to explain the line spectrum of hydrogen atom. The following are the assumptions (postulates) made by Bohr.

Postulates of Bohr atom model:

(a) The electron in an atom moves around nucleus in circular orbits under the influence of Coulomb electrostatic force of attraction. This Coulomb force gives necessary centripetal force for the electron to undergo circular motion.

(b) Electrons in an atom revolve around the nucleus only in certain discrete orbits called stationary orbits where it does not radiate electromagnetic energy. Only those discrete orbits allowed are stable orbits.

The angular momentum of the electron in these stationary orbits are quantized – that is, it can be written as integer or integral multiple of h / 2π called as reduced Planck’s constant – that is, h (read it as h-bar) and the integer n is called as principal quantum number of the orbit.

This condition is known as angular momentum quantization condition.

According to quantum mechanics, particles like electrons have dual nature (Refer unit 7, volume 2 of +2 physics text book). The standing wave pattern of the de Broglie wave associated with orbiting electron in a stable orbit is shown in Figure 8.15.

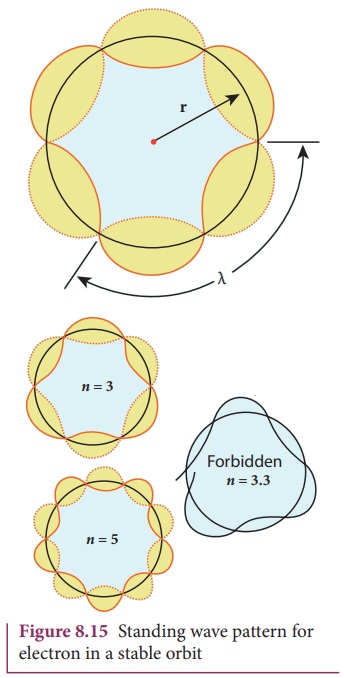
The circumference of an electron’s orbit of radius r must be an integral multiple of de Broglie wavelength – that is,

But the de Broglie wavelength (λ) for an electron of mass m moving with velocity υ is λ = h / mυ where h is called Planck’s constant.

Thus from equation (8.14),

For any particle of mass m undergoing circular motion with radius r and velocity υ, the magnitude of angular momentum l is given by

l = r(mυ)

mυr = l = nh

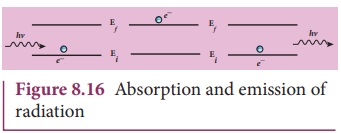
(c) Energy of orbits are not continuous but discrete. This is called the quantization of energy. An electron can jump from one orbit to another orbit by absorbing or emitting a photon whose energy is equal to the difference in energy (ΔE) between the two orbital levels (Figure 8.16)

∆E = E _final − E_initial = hv = h  c/λ

where c is the speed of light and λ is the wavelength of the radiation used and v is the frequency of the radiation. Thus, the frequency of the radiation emitted is related only to change in atom’s energy and it does not depend on frequency of electron’s orbital motion.

EXAMPLE 8.1

The radius of the 5th orbit of hydrogen atom is 13.25 Å. Calculate the wavelength of the electron in the 5th orbit.

Solution:

2πr = nλ

2 × 3.14 × 13.25Å = 5 × λ

 λ = 16.64Å

EXAMPLE 8.2

Find the (i) angular momentum (ii) velocity of the electron in the 5th orbit of hydrogen atom. (h = 6.6 × 10^–34 Js, m = 9.1 × 10^–31 kg)

Solution

Radius of the orbit of the electron and velocity of the electron

Consider an atom which contains the nucleus at rest and an electron revolving around the nucleus in a circular orbit of radius r_n as shown in Figure 8.17. Nucleus is made up of protons and neutrons. Since proton is positively charged and neutron is electrically neutral, the charge of a nucleus is purely the total charge of protons.

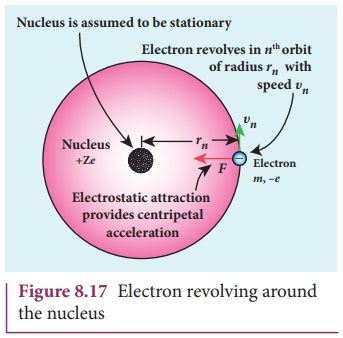
Let Z be the atomic number of the atom, then +Ze is the charge of the nucleus. Let –e be the charge of the electron. From Coulomb’s law, the force of attraction between the nucleus and the electron is

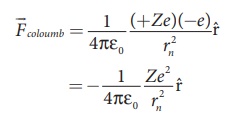
This force provides necessary centripetal force

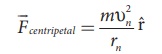
where m be the mass of the electron that moves with a velocity υ_n in a circular orbit. Therefore,

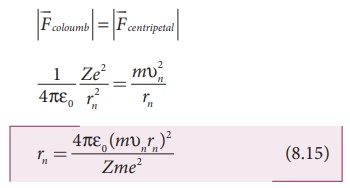
From Bohr’s assumption, the angular momentum quantization condition, mυ_nr_n = l_n = nh,

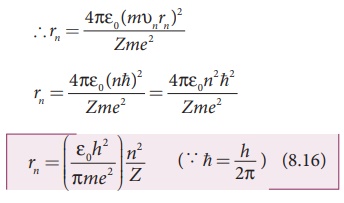
where n∈N . Since, ε₀, h, e and π are constants. Therefore, the radius of the orbit becomes

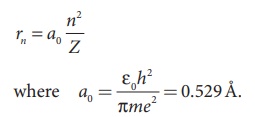
This is known as Bohr radius which is the smallest radius of the orbit in an atom. Bohr radius is also used as unit of length called Bohr. 1 Bohr = 0.53 Å. For hydrogen atom (Z = 1), the radius of nth orbit is

r_n = a₀n²

For n = 1 (first orbit or ground state),

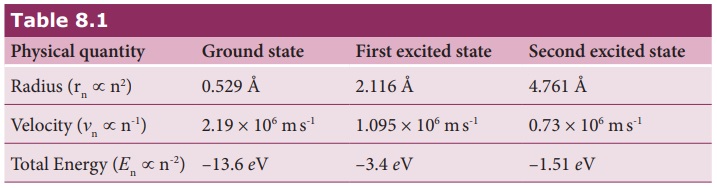
r₁ = a₀ = 0.529 Å

For n = 2 (second orbit or first excited state),

r₂ = 4a₀ = 2.116 Å

For n = 3 (third orbit or second excited state),

r₃ = 9a₀ = 4.761 Å

and so on.

Thus the radius of the orbit from centre increases with n, that is, r_n ∝ n² as shown in Figure 8.18.

Further, Bohr’s angular momentum quantization condition leads to

mυ_nr_n = mυ_na₀n² = n h/2π

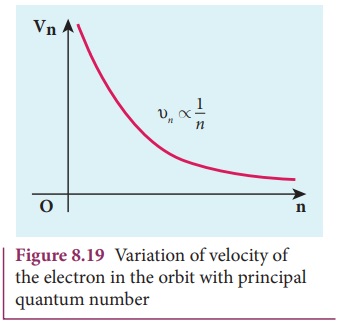
Note that the velocity of electron decreases as the principal quantum number increases as shown in Figure 8.19. This curve is the rectangular hyperbola. This implies that the velocity of electron in ground state is maximum when compared to excited states.

The energy of an electron in the nth orbit

Since the electrostatic force is a conservative force, the potential energy for the nth orbit is

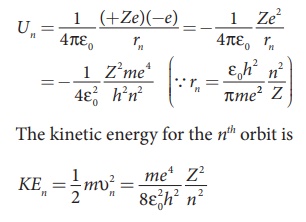
This implies that U_n = –2 KE_n. Total energy in the n^th orbit is

where n stands for principal quantum number. The negative sign in equation (8.17) indicates that the electron is bound to the nucleus.

Substituting the values of mass and charge of an electron (m and e), permittivity of free space ε₀ and Planck’s constant h and expressing in terms of eV, we get

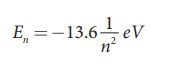
For the first orbit (ground state), the total energy of electron is E₁= – 13.6 eV.

For the second orbit (first excited state), the total energy of electron is E₂ = –3.4 eV. For the third orbit (second excited state), the total energy of electron is E₃ = –1.51 eV and so on.

Notice that the energy of the first excited state is greater than the ground state, second excited state is greater than the first excited state and so on. Thus, the orbit which is closest to the nucleus (r₁) has lowest energy (minimum energy compared with other orbits). So, it is often called ground state energy (lowest energy state). The ground state energy of hydrogen (–13.6 eV ) is used as a unit of energy called Rydberg (1 Rydberg = –13.6 eV ).

The negative value of this energy is because of the way the zero of the potential energy is defined. When the electron is taken away to an infinite distance (very far distance) from nucleus, both the potential energy and kinetic energy terms vanish and hence the total energy also vanishes.

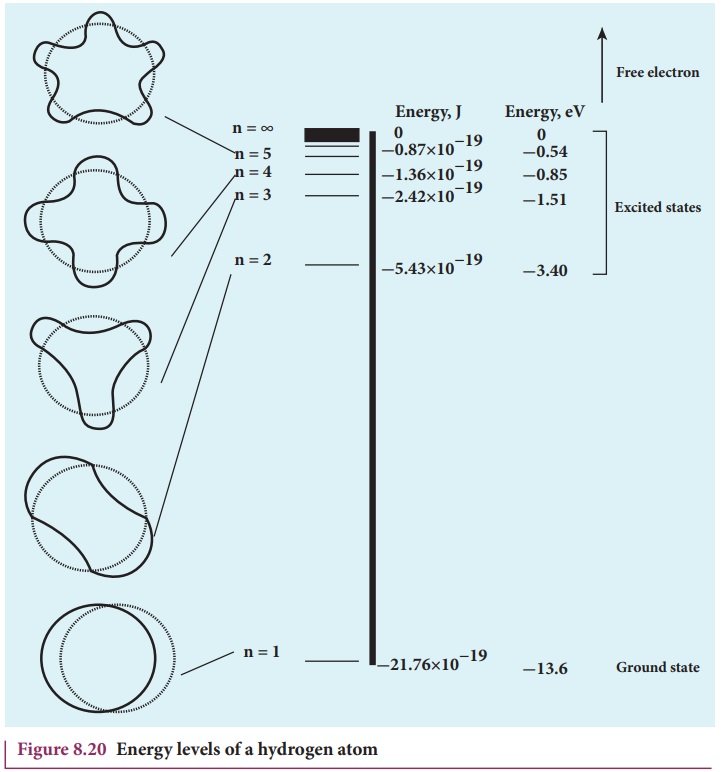
The energy level diagram along with the shape of the orbits for increasing values of n are shown in Figure 8.20. It shows that the energies of the excited states come closer and closer together when the principal quantum number n takes higher values.

EXAMPLE 8.3

(a) Show that the ratio of velocity of an electron in the first Bohr orbit to the speed of light c is a dimensionless number.

(b) Compute the velocity of electrons in ground state, first excited state and second excited state in Bohr atom model.

Solution

(a) The velocity of an electron in nth orbit is

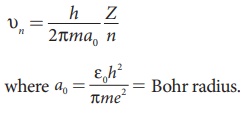
Substituting for a₀ in υ_n,

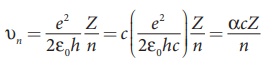
where c is the speed of light in free space or vacuum and its value is c = 3 × 10⁸ m s^–1and α is called fine structure constant.

For a hydrogen atom, Z = 1 and for the first orbit, n = 1, the ratio of velocity of electron in first orbit to the speed of light in vacuum or free space is

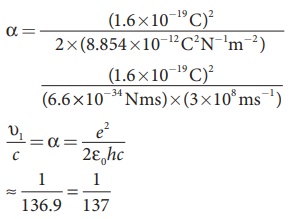
which is a dimensionless number

⇒ α = 1/137

(b) Using fine structure constant, the velocity of electron can be written as

υ_n = αcZ / n

For hydrogen atom (Z = 1) the velocity of electron in nth orbit is

υ_n = c/137 × 1/n = (2.19×10⁶) × 1/n  ms⁻¹

For the first orbit (ground state), the velocity of electron is

υ = 2.19×10⁶ ms⁻¹

For the second orbit (first excited state), the velocity of electron is

 υ₂ = 1.095×10⁶ ms⁻¹

For the third orbit (second excited state), the velocity of electron is

 υ₃ = 0.73×10⁶ ms⁻¹

Here, υ₁ > υ₂ > υ₃

EXAMPLE 8.4

The Bohr atom model is derived with the assumption that the nucleus of the atom is stationary and only electrons revolve around the nucleus. Suppose the nucleus is also in motion, then calculate the energy of this new system.

Solution

Let the mass of the electron be m and mass of the nucleus be M. Since there is no external force acting on the system, the centre of mass of hydrogen atom remains at rest. Hence, both nucleus and electron move about the centre of mass as shown in figure.

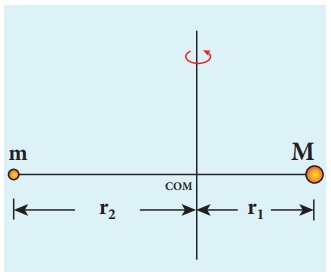
Let V be the velocity of the nuclear motion and υ be the velocity of electron motion. Since the total linear momentum of the system is zero,

−mυ + Mυ = 0 or

MV = mυ = p

Since the potential energy of the system is same, the total energy of the hydrogen can be expressed by replacing mass by reduced mass, which is

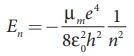
Since the nucleus is very heavy compared to the electron, the reduced mass is closer to the mass of the electron.

In 1931, H.C. Urey and co- workers noticed that in the shorter wavelength region of the hydrogen spectrum lines, faint companion lines are observed. From the isotope displacement effect (isotope shift), the isotope of the same element will have slightly different spectral lines. The presence of these faint lines confirmed the existence of isotopes of hydrogen atom (which is named as Deuterium).

On calculating wavelength or wave number difference between the faint and bright spectral lines, atomic mass of deuterium is measured to be twice that of atomic mass of hydrogen atom. Bohr atom model could not explain this isotopic shift. Thus by considering nuclear motion (although the movement of the nucleus is much smaller, it is observed) into account in the Bohr atom model, the wave number or wavelength difference between hydrogen atom and deuterium is theoretically calculated which perfectly agreed with the spectroscopic measured values.

The difference between hydrogen atom and deuterium is in the number of neutron. Hydrogen atom contains an electron and a proton, whereas deuterium has an electron, a proton and a neutron.

Excitation energy and excitation potential

The energy required to excite an electron from lower energy state to any higher energy state is known as excitation energy.

The excitation energy for an electron from ground state (n = 1) to first excited state (n = 2) is called first excitation energy, which is

E_I = E₂ – E₁ = –3.4 eV – (–13.6 eV) = 10.2 eV

Similarly, the excitation energy for an electron from ground state (n = 1) to second excited state (n = 3) is called second excitation energy, which is

E_u = E₃ – E₁ = –1.51 eV – (–13.6 eV) = 12.1 eV

and so on.

Excitation potential is defined as excitation energy per unit charge.

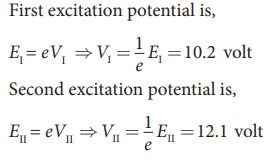
and so on.

Ionization energy and ionization potential

An atom is said to be ionized when an electron is completely removed from the atom – that is, it reaches the state with energy E_{n →∞}. The minimum energy required to remove an electron from an atom in the ground state is known as binding energy or ionization energy.

E_ionizaation = E_∞ - E₁ = 0 - (13.6eV)

= 13.6 eV

When an electron is in n^th state of an atom, the energy spent to remove an electron from that state – that is, its ionization energy is

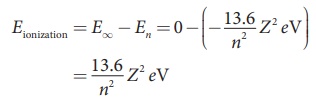
At normal room temperature, the electron in a hydrogen atom (Z=1) spends most of its time in the ground state. The amount of energy spent to remove an electron from the ground state of an atom (E = 0 for n→∞) is known as first ionization energy (13.6 eV).

Then, the hydrogen atom is said to be in ionized state or simply called as hydrogen ion, denoted by H⁺. If we supply more energy than the ionization energy, the excess energy will be the kinetic energy of the free electron.

Ionization potential is defined as ionization energy per unit charge.

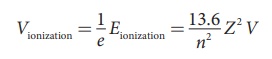
Thus, for a hydrogen atom (Z =1), the ionization potential is

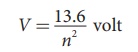
The radius, velocity and total energy in ground state, first excited state and second excited state is listed in Table 8.1.

EXAMPLE 8.5

Suppose the energy of a hydrogen–like atom is given as E_n = − 54.4/n² eV where n∈N . Calculate the following:

(a) Sketch the energy levels for this atom and compute its atomic number.

(b) If the atom is in ground state, compute its first excitation potential and also its ionization potential.

(c) When a photon with energy 42 eV and another photon with energy 56 eV are made to collide with this atom, does this atom absorb these photons?

(d) Determine the radius of its first Bohr orbit.

(e) Calculate the kinetic and potential energies in the ground state.

Solutions

(a) Given that

E_n =− 54.4/n² eV

For n = 1, the ground state energy E₁= –54.4 eV and for n = 2, E₂ = –13.6 eV.

Similarly, E₃ = –6.04 eV, E₄ = –3.4 eV and so on.

For large value of principal quantum number – that is, n = ∞, we get E_∞ = 0 eV.

(b) For a hydrogen-like atom, ground state energy is

E₁ = − 13.6/n² Z² eV

where Z is the atomic number. Hence, comparing this energy with given energy, we get, – 13.6 Z² = – 54.4 ⇒ Z = ±2. Since, atomic number cannot be negative number, Z = 2.

(c) The first excitation energy is

E_I = E₂ − E₁ = −13.6eV −(−54.4 eV)

 = 40.8eV

Hence, the first excitation potential is

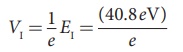
= 40.8 volt

The first ionization energy is

E_ionization = E_∞ − E₁ = 0 −(−54.4 eV)

= 54.4 eV

Hence, the first ionization potential is

V_ionization = 1/e E_ionization = (54.4eV)/e

= 54.4 Volt

(d) Consider two photons to be A and B.

Given that photon A with energy 42 eV and photon B with energy 51 eV

From Bohr assumption, difference in energy levels is equal to photon energy, then atom will absorb energy, otherwise, not.

E₂ − E₁ = −13.6eV −(−54.4 eV)

= 40.8eV ≈ 41eV

Similarly,

E₃ − E₁ = −6.04 eV −(−54.4 eV)

= 48.36eV

E₄ − E₁ = −3.4 eV −(−54.4 eV)

= 51eV

E₃ − E₂ = −6.04 eV −(−13.6eV)

= 7.56eV

and so on.

But note that E₂ – E₁ ≠ 42 eV, E₃ – E₁ ≠ 42 eV, E₄ – E₁ ≠ 42 eV and E₃ – E₂ ≠ 42 eV.

For all possibilities, no difference in energy is an integer multiple of photon energy. Hence, photon A is not absorbed by this atom. But for Photon B, E₄ – E₁ = 51 eV, which means, Photon B can be absorbed by this atom.

(e) Since total energy is equal to negative of kinetic energy in Bohr atom model, we get

KE_n = −E_n = −( − 54.4/n² eV)

 = 54.4/n² eV

Potential energy is negative of twice the kinetic energy, which means,

U_n = −2KE_n = −2(54.4/n² eV)

= −108.8/n² eV

For a ground state, put n =1

Kinetic energy is KE₁ = 54.4 eV and Potential energy is U₁ = –108.8 eV