Radioactivity: Alpha decay

Alpha decay

When unstable nuclei decay by emitting an α-particle ( ⁴₂He nucleus), it loses two protons and two neutrons. As a result, its atomic number Z decreases by 2, the mass number decreases by 4. We write the alpha decay process symbolically in the following way

Here X is called the parent nucleus and Y is called the daughter nucleus.

Example: Decay of Uranium ²³⁸₉₂U to thorium ²³⁴₉₀Th with the emission of ⁴₂He nucleus (α-particle)

²³⁸₉₂U → ²³⁴₉₀Th + ⁴₂He

As already mentioned, the total mass of the daughter nucleus and ⁴₂He nucleus is always  less than that of the parent nucleus. The difference in mass ( ∆m = m_X − m_Y − m_α ) is released as energy called disintegration energy Q and is given by

Q = (m_X − m_Y − m_α )c²           (8.27)

Note that for spontaneous decay (natural radioactivity) Q >0. In alpha decay process, the disintegration energy is certainly positive (Q > 0). In fact, the disintegration energy Q is also the net kinetic energy gained in the decay process or if the parent nucleus is at rest, Q is the total kinetic energy of daughter nucleus and the ⁴₂He nucleus. Suppose Q < 0, then the decay process cannot occur spontaneously and energy must be supplied to induce the decay.

In alpha decay, why does the unstable nucleus emit ⁴₂He nucleus? Why it does not emit four separate nucleons? After all He consists of two protons and two neutrons. For example, if ₉₂²³⁸U nucleus decays into ₉₀²³⁴Th by emitting four separate nucleons (two protons and two neutrons), then the disintegration energy Q for this process turns out to be negative. It implies that the total mass of products is greater than that of parent( ⁹²₂₃₈U ) nucleus.

This kind of process cannot occur in nature because it would violate conservation of energy. In any decay process, the conservation of energy, conservation of linear momentum and conservation of angular momentum must be obeyed.

EXAMPLE 8.11

(a) Calculate the disintegration energy when stationary ²³²₉₂U nucleus decays to thorium ²²⁸₉₀Th with the emission of α particle. The atomic masses are of ²³²₉₂U = 232.037156 u , ²²⁸₉₀Th = 228.028741u and ⁴₂He = 4.002603u

(b) Calculate kinetic energies of ²²⁸₉₀Th and α-particle and their ratio.

Solution

The difference in masses

∆m = (m_U – m_Th - m_α)

= (232.037156–228.028741 – 4.002603)u

The mass lost in this decay = 0.005812 u

Since 1u = 931MeV, the energy Q released is

Q = (0.005812u)×(931MeV / u)

= 5.41MeV

This disintegration energy Q appears as the kinetic energy of α particle and the daughter nucleus.

In any decay, the total linear momentum must be conserved.

Total linear momentum of the parent nucleus = total linear momentum of the daughter nucleus +α particle

Since before decay, the uranium nucleus is at rest, its momentum is zero.

By applying conservation of momentum, we get

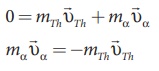
It implies that the alpha particle and daughter nucleus move in opposite directions.

In magnitude m_α υ_α = m_Thυ_Th

The velocity α particle Ï…_α =  [m_Th/m_α] Ï…_Th.

Note that m_Th /m_a > 1, so υ_α > υ_Th . The ratio of the kinetic energy of α particle to the daughter nucleus

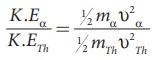
By substituting, the value of υ_α into the above equation, we get

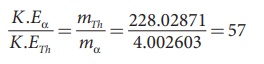
The kinetic energy of α particle is 57 times greater than the kinetic energy of the daughter nucleus (²²⁸₉₀Th ).

The disintegration energy Q = total kinetic energy of products

K.E_α + K.E_Th = 5.41MeV

57K.E_Th + K.E_Th = 5.41MeV

K.E_Th = 5.41/58 MeV = 0.093MeV

K.E_α = 57K.E_Th = 57×0.093 = 5.301MeV

In fact, 98% of total kinetic energy is taken by the α particle.