Half-life

Half-life

It is difficult to calculate the time taken by a given a sample of N atoms to decay. However, we can calculate the time taken by the given sample of atoms to reduce some fraction of the initial amount.

We can define the half-life T_1/2 as the time required for the number of atoms initially present to reduce to one half of the initial amount.

The half-life is the important characteristic of every radioactive sample. Some radioactive nuclei are known to have half-life as long as 10¹⁴ years and some nucleus have very shorter life time (10^-14s).

We can express half-life in terms of the decay constant. At t = T_1/2 , the number of undecayed nuclei N = N₀/2 .

By substituting this value in to the equation (8.35), we get

N₀/2 = N₀ e^{−λT1/2}

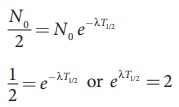
Taking logarithm on both sides and rearranging the terms,

One should not think that shorter half-life material is safer than longer half-life material because it will not last long. The shorter half-life sample will have higher activity and it is more ‘radioactive’ which is more harmful.

If the number of atoms present at t=0 is N₀, then N₀/2 atoms remain undecayed in first half-life and N₀/4 atoms remain undecayed after second half life and so on. In general, after n half-lives, the number of nuclei remaining undecayed is given by

where n can be integer or non-integer.

Since the activity of radioactive sample also obeys the exponential decay law, we can also write an equation for an activity similar to equation (8.36).

After n half-lives, the activity or decay rate of any radioactive sample is

Mean life (Ï„):

When the radioactive nucleus undergo the decay, the nucleus which disintegrates first has zero life time and the nucleus which decay last has an infinite lifetime. The actual life time for each nucleus varies from zero to infinity. Therefore, it is meaningful to define average life or mean life time Ï„, that the nucleus survives before it decays.

The mean life time of the nucleus is the ratio of sum or integration of life times of all nuclei to the total number nuclei present initially.

The total number of nuclei decaying in the time interval from t to t + ∆t is equal to R∆t = λN₀ e^−λt ∆t. It implies that until the time t, this R∆t number of nuclei lived. So the life time of these R∆t nuclei is equal to be tR∆t . In the limit ∆t → 0 , the total life time of all the nuclei would be the integration of tRdt from the limit t = 0 to t = ∞ .

Mean life

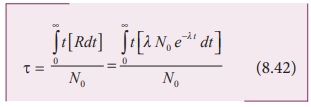
After a few integration (refer box item), the expression for mean life time,

Note that mean life and decay constant is inversely proportional to each other.

Using mean life, the half-life can be rewritten as

T_1/2 = Ï„ ln 2 = 0.6931Ï„ (8.44)

Mean life : Not for examination

The integration in the equation (8.42) can be performed using integration by parts.

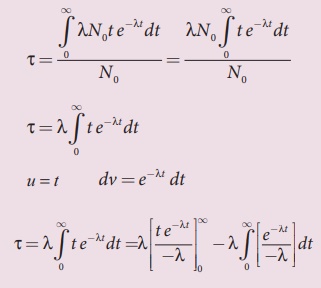
By substituting the limits, the first term in the above equation becomes zero.

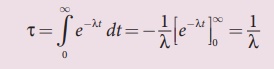
EXAMPLE 8.12

Calculate the number of nuclei of carbon-14 undecayed after 22,920 years if the initial number of carbon-14 atoms is 10,000. The half-life of carbon-14 is 5730 years.

Solution

To get the time interval in terms of half- life,

The number of nuclei remaining undecayed after 22,920 years,

N = ( ½ )⁰ N₀ = (1/2)⁴ ×10, 000

N = 625

EXAMPLE 8.13

A radioactive sample has 2.6 μg of pure ¹³₇N which has a half-life of 10 minutes (a) How many nuclei are present initially? (b) What is the activity initially? (c) What is the activity after 2 hours? (d) Calculate mean life of this sample.

Solution

(a) To find N₀, we have to find the number of ¹³₇N atoms in 2.6μg . The atomic mass of nitrogen is 13. Therefore, 13 g of ¹³₇N contains Avogadro number ( 6.02 ×10²³ ) of atoms.

In 1 g, the number of ¹³₇N is equal to be 6.02×10²³ / 13 atoms. So the number of ¹³₇N atoms in 2.6μg is

N = (6.02×10²³/13) × 2.6×10^−6 = 12.04×10¹⁶ atoms

(b) To find the initial activity R₀, we have to evaluate decay constant λ

λ = 0.6931 / T_1/2 = 0.6931 / 10×60 = 1.155×10^−3 s^−1

Therefore

R₀ = λN₀ = 1.155×10^-3 ×12.04×10¹⁶

=13.90×10¹³ decays/s

= 13.90×10¹³ Bq

In terms of a curie,

R₀ = 13.90×10¹⁵ / 3.7×10¹⁰ = 3.75×10³ Ci

since 1Ci = 3.7×10¹⁰Bq

(c) Activity after 2 hours can be calculated in two different ways:

Method 1: R = R₀e^{–λt}

At t = 2 hr = 7200 s

R = 3.75 × 10³ × e^{–7200 ×1.155 ×10–3}

R = 3.75 × 10³ × 2.4 ×10^–4 = 0.9 Ci

Method 2: R = (1/2)ⁿ R₀

Here n = 120 min /10 min  = 12

R = (1/2)¹² ×3.75×10³ ≈ 0.9Ci

(d) mean life Ï„ = T_1/2  / 0.6931 = 10×60 / 0.6931

  = 865.67 s