Determination of charge of an electron - Millikan’s oil drop experiment

Determination of charge of an electron – Millikan’s oil drop experiment

Millikan’s oil drop experiment is another important experiment in modern physics which is used to determine one of the fundamental constants of nature known as charge of an electron (Figure 8.6 (a)).

By adjusting electric field suitably, the motion of oil drop inside the chamber can be controlled – that is, it can be made to move up or down or even kept balanced in the field of view for sufficiently long time.

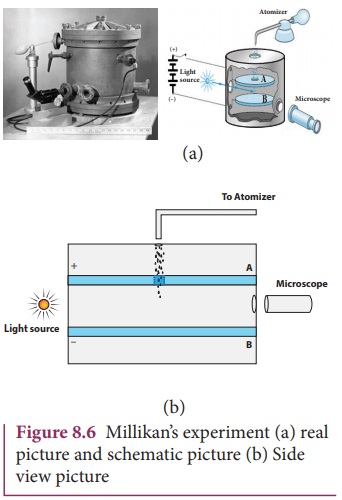
The experimental arrangement is shown in Figure 8.6 (b). The apparatus consists of two horizontal circular metal plates A and B each with diameter around 20 cm and are separated by a small distance 1.5 cm.

These two parallel plates are enclosed in a chamber with glass walls. Further, plates A and B are given a high potential difference around 10 kV such that electric field acts vertically downward. A small hole is made at the centre of the upper plate A and atomizer is kept exactly above the hole to spray the liquid. When a fine droplet of highly viscous liquid (like glycerine) is sprayed using atomizer, it falls freely downward through the hole of the top plate only under the influence of gravity.

Few oil drops in the chamber can acquire electric charge (negative charge) because of friction with air or passage of x-rays in between the parallel plates. Further the chamber is illuminated by light which is passed horizontally and oil drops can be seen clearly using microscope placed perpendicular to the light beam. These drops can move either upwards or downward.

Let m be the mass of the oil drop and q be its charge. Then the forces acting on the droplet are

(a) gravitational force F_g = mg

(b) electric force F_e = qE

(c) buoyant force F_b

(d) Viscous force F_v

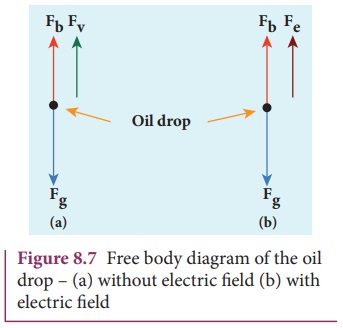
(a) Determination of radius of the droplet

When the electric field is switched off, the oil drop accelerates downwards. Due to the presence of air drag forces, the oil drops easily attain its terminal velocity and moves with constant velocity. This velocity can be carefully measured by noting down the time taken by the oil drop to fall through a predetermined distance. The free body diagram of the oil drop is shown in Figure 8.7 (a), we note that viscous force and buoyant force balance the gravitational force.

Let the gravitational force acting on the oil drop (downward) be F_g = mg

Let us assume that oil drop to be spherical in shape. Let ρ be the density of the oil drop, and r be the radius of the oil drop, then the mass of the oil drop can be expressed in terms of its density as

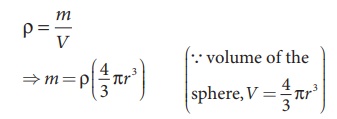
The gravitational force can be written in terms of density as

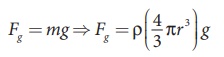
Let σ be the density of the air, the upthrust force experienced by the oil drop due to displaced air is

Once the oil drop attains a terminal velocity υ, the net downward force acting on the oil drop is equal to the viscous force acting opposite to the direction of motion of the oil drop. From Stokes law, the viscous force on the oil drop is

F_v =6πrυη

From the free body diagram as shown in Figure 8.7 (a), the force balancing equation is

Thus, equation (8.11) gives the radius of the oil drop.

(b) Determination of electric charge

When the electric field is switched on, charged oil drops experience an upward electric force (qE). Among many drops, one particular drop can be chosen in the field of view of microscope and strength of the electric field is adjusted to make that particular drop to be stationary. Under these circumstances, there will be no viscous force acting on the oil drop. Then, from the free body diagram shown Figure 8.7 (b), the net force acting on the oil droplet is

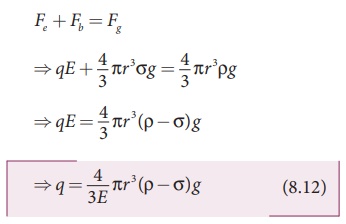
Substituting equation (8.11) in equation (8.12), we get

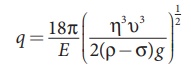
Millikan repeated this experiment several times and computed the charges on oil drops. He found that the charge of any oil drop can be written as integral multiple of a basic value, −1.6×10⁻¹⁹C, which is nothing but the charge of an electron.