Chapter: 11th Physics : UNIT 3 : Laws of Motion
Newton’s Law
NEWTON’S LAWS
Newton
analysed the views of Galileo, and other scientist like Kepler and Copernicus
on motion and provided much deeper insights in the form of three laws.
Newton’s First Law
Every
object continues to be in the state of rest or of uniform motion (constant
velocity) unless there is external force acting on it.
This
inability of objects to move on its own or change its state of motion is called
inertia. Inertia means resistance to change its state. Depending on the
circumstances, there can be three types of inertia.
1. Inertia of rest: When a stationary bus starts to move, the passengers
experience a sudden backward push. Due to inertia, the body (of a passenger)
will try to
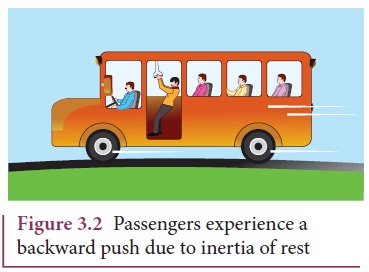
continue
in the state of rest, while the bus moves forward. This appears as a backward
push as shown in Figure 3.2. The
inability of an object to change its state of rest is called inertia of rest.
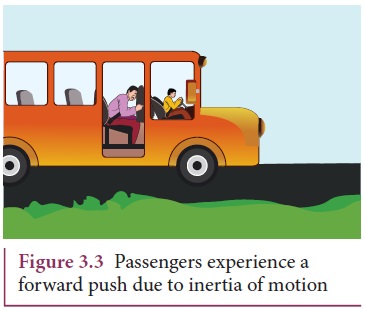
2. Inertia of motion: When the bus is in motion, and if the brake is applied suddenly, passengers move
forward and hit against the front seat. In this case, the bus comes to a stop,
while the body (of a passenger) continues to move forward due to the property
of inertia as shown in Figure 3.3. The
inability of an object to change its
state of uniform speed (constant speed) on its own is called inertia of motion.
3. Inertia of direction: When a stone attached to a string is in whirling
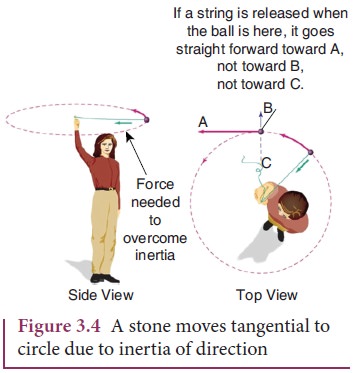
This is because the body cannot change its direction of motion without any
force acting on it. The inability of an
object to change its direction of
motion on its own is called inertia of direction.
When we say that an object is at rest or in motion with constant velocity, it has a meaning only if it is specified with respect to some reference frames. In physics, any motion has to be stated with respect to a reference frame. It is to be noted that Newton’s first law is valid only in certain special reference frames called inertial frames. In fact, Newton’s first law defines an inertial frame.
Inertial Frames
If
an object is free from all forces, then it moves with constant velocity or
remains at rest when seen from inertial frames. Thus, there exists some special
set of frames in which if an object experiences no force it moves with constant
velocity or remains at rest. But how do we know whether an object is experiencing
a force or not? All the objects in the Earth experience Earth’s gravitational
force. In the ideal case, if an object is in deep space (very far away from any
other object), then Newton’s first law will be certainly valid. Such deep space
can be treated as an inertial frame. But practically it is not possible to
reach such deep space and verify Newton’s first law.
For
all practical purposes, we can treat Earth as an inertial frame because an
object on the table in the laboratory appears to be at rest always. This object
never picks up acceleration in the horizontal direction since no force acts on
it in the horizontal direction. So the laboratory can be taken as an inertial
frame for all physics experiments and calculations. For making these conclusions,
we analyse only the horizontal motion of the object as there is no horizontal
force that acts on it. We should not analyse the motion in vertical direction
as the two forces (gravitational force in the downward direction and normal
force in upward direction) that act on it makes the net force is zero in
vertical direction. Newton’s first law deals with the motion of objects in the
absence of any force and not the motion under zero net force. Suppose a train
is moving with constant velocity with respect to an inertial frame, then an
object at rest in the inertial frame (outside the train) appears to move with
constant velocity with respect to the train (viewed from within the train). So
the train can be treated as an inertial frame. All inertial frames are moving with
constant velocity relative to each other. If an object appears to be at rest in
one inertial frame, it may appear to move with constant velocity with respect
to another inertial frame. For example, in Figure 3.5, the car is moving with
uniform velocity v with respect to a
person standing (at rest) on the ground. As the car is moving with constant
velocity with respect to ground to the person is at rest on the ground, both
frames (with respect to the car and to the ground) are inertial frames.

Suppose
an object remains at rest on a smooth table kept inside the train, and if the
train suddenly accelerates (which we may not sense), the object appears to
accelerate backwards even without any force acting on it. It is a clear
violation of Newton’s first law as the object gets accelerated without being
acted upon by a force. It implies that the train is not an inertial frame when
it is accelerated. For example, Figure 3.6 shows that car 2 is a non-inertial
frame since it moves with acceleration ![]() with respect to the ground.
with respect to the ground.
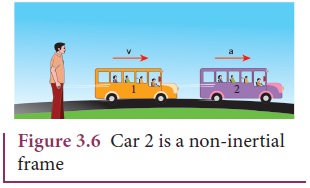
These
kinds of accelerated frames are called non-inertial frames. A rotating frame is
also a non inertial frame since rotation requires acceleration. In this sense,
Earth is not really an inertial frame since it has self-rotation and orbital
motion. But these rotational effects of Earth can be ignored for the motion
involved in our day-to-day life. For example, when an object is thrown, or the
time period of a simple pendulum is measured in the physics laboratory, the
Earth’s self-rotation has very negligible effect on it. In this sense, Earth
can be treated as an inertial frame. But at the same time, to analyse the
motion of satellites and wind patterns around the Earth, we cannot treat Earth
as an inertial frame since its self-rotation has a strong influence on wind
patterns and satellite motion.
Newton’s Second Law
This
law states that
The force acting on an object is
equal to the rate of change of its momentum
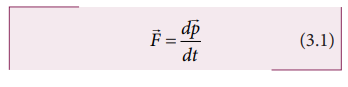
In
simple words, whenever the momentum of the body changes, there must be a force
acting on it. The momentum of the object is defined as 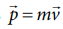 . In most cases, the mass
of the object remains constant during the motion. In such cases, the above
equation gets modified into a simpler form
. In most cases, the mass
of the object remains constant during the motion. In such cases, the above
equation gets modified into a simpler form

The
above equation conveys the fact that if there is an acceleration a on the body, then there must be a
force acting on it. This implies that if there is a change in velocity, then there
must be a force acting on the body. The force and acceleration are always in
the same direction. Newton’s second law was a paradigm shift from Aristotle’s
idea of motion. According to Newton, the force need not cause the motion but
only a change in motion. It is to be noted that Newton’s second law is valid
only in inertial frames. In
non-inertial frames Newton’s second law cannot be used in this form. It
requires some modification.
In
the SI system of units, the unit of force is measured in newtons and it is
denoted by symbol ‘N’.
One Newton is defined as the force
which acts on 1 kg of mass to give an acceleration 1 m s-2 in the direction of the force.
Aristotle vs. Newton’s approach on sliding object
Newton’s
second law gives the correct explanation for the experiment on the inclined
plane that was discussed in section 3.1. In normal cases, where friction is not
negligible, once the object reaches the bottom of the inclined plane (Figure
3.1), it travels some distance and stops. Note that it stops because there is a
frictional force acting in the direction opposite to its velocity. It is this
frictional force that reduces the velocity of the object to zero and brings it
to rest. As per Aristotle’s idea, as soon as the body reaches the bottom of the
plane, it can travel only a small distance and stops because there is no force
acting on the object. Essentially, he did not consider the frictional force
acting on the object.

Newton’s
Third Law
Consider
Figure 3.8(a) whenever an object 1 exerts a force on the object 2 (![]() ), then object 2 must also
exert equal and opposite force on the object 1 (
), then object 2 must also
exert equal and opposite force on the object 1 (![]() ). These forces must lie along the line joining the
two objects.
). These forces must lie along the line joining the
two objects.
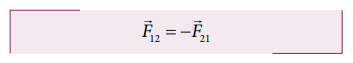
Newton’s
third law assures that the forces occur as equal and opposite pairs. An
isolated force or a single force cannot exist in nature. Newton’s third law states that
for every action there is an equal and opposite reaction. Here, action and
reaction pair of forces do not act on
the same body but on two different bodies. Any one of the forces can be called
as an action force and the other the reaction force. Newton’s third law is
valid in both inertial and non-inertial frames.
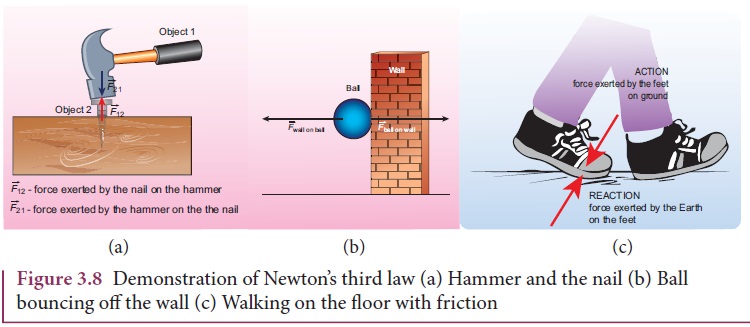
These action-reaction forces are not cause and effect forces. It means that when the object 1 exerts force on the object 2, the object 2 exerts equal and opposite force on the body 1 at the same instant.
Discussion on Newton’s Laws
1.
Newton’s laws are vector laws. The equation 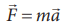 is a vector
equation and essentially it is equal to three scalar equations. In Cartesian
coordinates, this equation can be written as
is a vector
equation and essentially it is equal to three scalar equations. In Cartesian
coordinates, this equation can be written as

By
comparing both sides, the three scalar equations are
Fx = max The acceleration along the x direction depends only on the component
of force acting along the x-direction.
Fy = may The acceleration along the y direction depends only on the component
of force acting along the y-direction.
Fz = maz The acceleration along the z direction depends only on the component
of force acting along the z-direction.
From
the above equations, we can infer that the force acting along y direction
cannot alter the acceleration along x direction. In the same way, Fz cannot afect ay and ax . This understanding is essential for solving
problems.
2.
The acceleration experienced by the body at time t depends on the force which
acts on the body at that instant of time. It does not depend on the force which
acted on the body before the time t. This can be expressed as
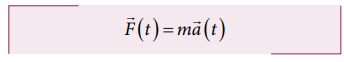
Acceleration
of the object does not depend on the previous history of the force. For
example, when a spin bowler or a fast bowler throws the ball to the batsman,
once the ball leaves the hand of the bowler, it experiences only gravitational
force and air frictional force. The acceleration of the ball is independent of
how the ball was bowled (with a lower or a higher speed).
3.
In general, the direction of a force may be different from the direction of
motion. Though in some cases, the object may move in the same direction as the
direction of the force, it is not always true. A few examples are given below.
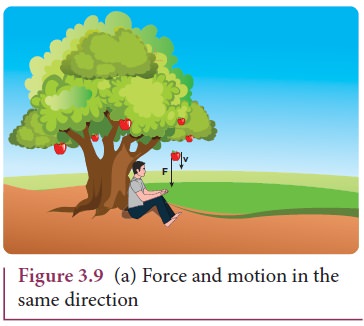
Case 1: Force and motion in the same direction
When
an apple falls towards the Earth, the direction of motion (direction of
velocity) of the apple and that of force are in the same downward direction as
shown in the Figure 3.9 (a).
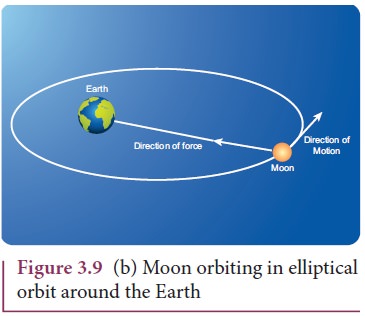
Case 2: Force and motion not in the same direction
The
Moon experiences a force towards the Earth. But it actually moves in elliptical
orbit. In this case, the direction of the force is different from the direction
of motion as shown in Figure 3.9 (b).
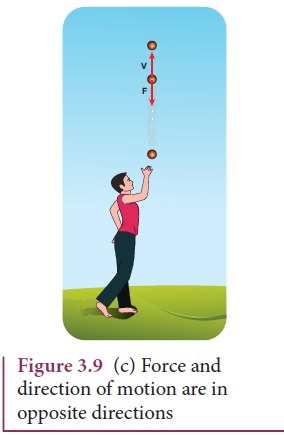
Case 3: Force and motion in opposite direction
If
an object is thrown vertically upward, the direction of motion is upward, but
gravitational force is downward as shown in the Figure 3.9 (c).
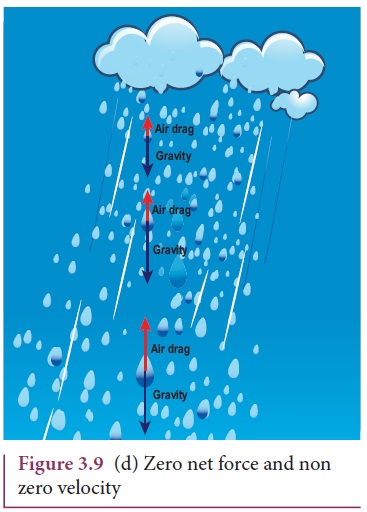
Case 4: Zero net force, but there is
motion When a
raindrop gets detached from the cloud it experiences both downward
gravitational force and upward air drag force. As it descends towards the
Earth, the upward air drag force increases and after a certain time, the upward
air drag force cancels the downward gravity. From then on the raindrop moves at
constant velocity till it touches the surface of the Earth. Hence the raindrop
comes with zero net force, therefore with zero acceleration but with non-zero
terminal velocity. It is shown in the Figure 3.9 (d).
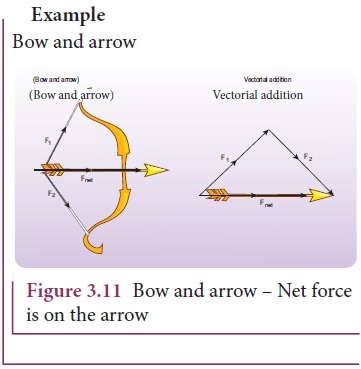
4.
If multiple forces .![]() 1 ,
1 ,![]() 2 ,
2 ,![]() 3 ...
3 ... ![]() n act on the same body, then the total
force (
n act on the same body, then the total
force (![]() net )
is equivalent to the vectorial sum of the individual forces. Their net force
provides the acceleration.
net )
is equivalent to the vectorial sum of the individual forces. Their net force
provides the acceleration.

In
this case the direction of acceleration is in the direction of net force.
5.
Newton’s second law can also be written in the following form.
Since
the acceleration is the second derivative of position vector of the body
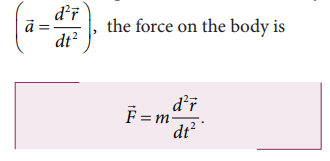
From
this expression, we can infer that Newton’s second law is basically a second
order ordinary differential equation and whenever the second derivative of
position vector is not zero, there must be a force acting on the body.
6.
If no force acts on the body then Newton’s second law,
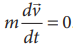
It
implies that ![]() = constant. It is
essentially Newton’s first law. It implies that the second law is consistent
with the first law. However, it should not be thought of as the reduction of
second law to the first when no force acts on the object. Newton’s first and
second laws are independent laws. They can internally be consistent with each
other but cannot be derived from each other.
= constant. It is
essentially Newton’s first law. It implies that the second law is consistent
with the first law. However, it should not be thought of as the reduction of
second law to the first when no force acts on the object. Newton’s first and
second laws are independent laws. They can internally be consistent with each
other but cannot be derived from each other.
7.
Newton’s second law is cause and effect relation. Force is the cause and
acceleration is the effect. Conventionally, the effect should be written on the
left and cause on the right hand side of the equation. So the correct way of
writing Newton’s second law is
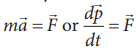
Related Topics