Algebra

UNIT 3

ALGEBRA

Learning Objectives

• To recall addition and subtraction of expressions.

• To know how to multiply algebraic expressions with integer co-efficients

• To know how to divide algebraic expressions by monomials.

• To recall the identities (a + b)² ,(a − b)² ,(a ² − b² ) and (x + a)(x + b) and able to apply them in problems.

• To understand the identities (a + b)³ ,(a − b)³ ,(x + a)(x + b)(x + c) and apply them in problems.

• To recognize expressions that are factorizable of the type (a + b)³ and (a − b)³ .

• To solve word problems that involve linear equations.

• To know how to plot the points in the graph.

• To draw graphs of simple linear equations.

Recap

In our earlier classes, we have learnt about constants, variables, like terms, unlike terms, co-efficients, numerical and algebraic expressions. Later, we have done some basic operations like addition and subtraction on algebraic expressions. Now, we shall recollect them and extend the learning.

Further, we are going to learn about multiplication and division of algebraic expressions and algebraic identities.

Answer the following questions :

1. Write the number of terms in the following expressions

(i) x + y + z − xyz [Answer: 4 terms]

(ii) m²n²c [Answer: 1 term]

(iii) a²b²c − ab²c² + a²bc² + 3abc [Answer: 4 terms]

(iv) 8x² − 4xy + 7xy² [Answer: 3 terms]

2. Identify the numerical co-efficient of each term in the following expressions.

(i) 2x² − 5xy + 6 y² + 7x −10 y + 9

(ii) x/3 + 2y/5 − xy + 7

(i) 2x² − 5xy + 6y² + 7x − 10y + 9

Answer:

Numerical co efficient in 2x² is 2

Numerical co efficient in −5xy is −5

Numerical co efficient in 6y² is 6

Numerical co efficient in 7x is 7

Numerical co efficient in −10y is − 10

Numerical co−efficient in 9 is 9

(ii) x/3 + 2y/5 − xy + 7

Answer:

Numerical co efficient in x/3 is 1/3

Numerical co efficient in 2y/5 is 2/5

Numerical co efficient in −xy is −1

Numerical co efficient in 7 is 7

3. Pick out the like terms from the following:

Solution:

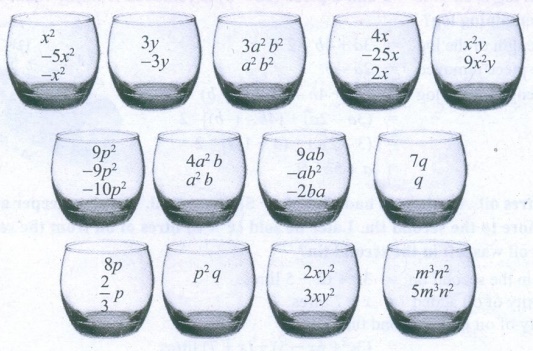
4. Add : 2x , 6 y, 9x − 2y

Solution:

2x + 6y + 9x − 2y = 2x + 9x + 6y − 2y = (2 + 9)x + (6 − 2)y = 11x + 4y

5. Simplify : (5x ³ y³ − 3x ² y² + xy + 7) + (2xy + x ³ y³ − 5 + 2x ² y² )

Solution:

(5x³y³ − 3x²y² + xy + 7) + (2xy + x³y³ − 5 + 2x²y²)

= 5x³y³ + x³y³ – 3x²y² + 2x²y² + xy + 2xy + 7 − 5

= (5 + 1) x³y³ + (−3 + 2) x²y² + (1 + 2) xy + 2

= 6 x³y³ − x²y² + 3xy + 2

6. The sides of a triangle are 2x − 5y + 9, 3y + 6x − 7 and −4 x + y + 10 . Find the perimeter of the triangle .

Solution:

Perimeter of the triangle = Sum of three sides

= (2x − 5y + 9) + (3y + 6x −7) + (−4x + y + 10)

= 2x − 5y + 9 + 3y + 6x − 7 − 4x + y + 10

= 2x + 6x − 4x − 5y + 3y + y + 9 − 7 + 10

= (2 + 6 − 4)x + (−5 + 3 + l) y + (9 − 7 + 10)

= 4x –y + 12

∴  Perimeter of the triangle = 4x –y + 12 units.

7. Subtract −2mn from 6mn.

Solution:

6 mn − (−2 mn) = 6 mn + (+2 mn)

= (6 + 2) mn = 8 mn

8. Subtract 6a ² − 5ab + 3b² from 4a ² − 3ab + b² .

Solution:

(4a² − 3ab + b²) − (6a^{2 −} 5ab + 3b²)

= (4a² − 6a²) + (− 3ab − (−5 ab)] + (b² − 3b²)

= (4 − 6) a² + [−3ab + (+5 ab)] + (1 − 3) b²

= [4 + (− 6)] a² + (−3 + 5) ab + [1+ (−3)] b²

= −2a² + 2ab − 2b²

9. The length of a log is 3a + 4b − 2 and a piece (2a − b) is removed from it. What is the length of the remaining log?

Solution:

Length of the log = 3a + 4b − 2

Length of the piece removed = 2a − b

Remaining length of the log = (3a + 4b −2) − (2a − b)

= (3a – 2a) + [4b − (− b)] − 2

= (3 − 2)a + (4 + 1)b − 2

= a + 5b – 2

10. A tin had x litres of oil. Another tin had (3x² + 6x − 5) litres of oil.

The shopkeeper added (x+7) litres more to the second tin. Later, he sold (x²+6) litres of oil from the second tin. How much oil was left in the second tin?

Solution:

Quantity of oil in the second tin = 3x² + 6x − 5 litres.

Quantity of oil added = x + 7 litres

∴  Total quantity of oil in the second tin

= (3x² + 6x − 5) + (x + 7) litres

= 3x² + (6x + x) + (−5 + 7) = 3x² + (6 + 1 )x + 2

= 3x² + 7x + 2 litres

Quantity of oil sold = x² + 6 litres

∴ Quantity of oil left in the second tin

= (3x² + 7x + 2) − (x² + 6) = (3x² − x²) + 7x + (2 − 6)

= (3 − 1) x² + 7x + (−4) = 2x² + 7x − 4

Quantity of oil left = 2x² + 7x − 4 litres

MATHEMATICS ALIVE – ALGEBRA IN REAL LIFE

Introduction

Let us consider the given situation that Ganesh planted saplings in his garden. He planted 10 rows each with 5 saplings. Can you say how many saplings were planted?

Yes, we know that, the total number of saplings is the product of number of rows and number of saplings in each row.

Hence, the total number of saplings = 10 rows × 5 saplings in each row = 10 × 5 =50 saplings

Likewise, David planted some saplings. Not knowing the total number of rows and saplings in each row, how will you express the total number of saplings?

For the unknown quantities, we call them as ‘x’ and ‘y’. Therefore, the total number of saplings = ‘x’ rows × ‘y’ sapling in each row

 = ‘x × y’ = xy saplings

Let us extend this situation, Rahim planted saplings where the number of rows are (2x² + 5x − 7) and each row contains 3y ² saplings. Now the above idea will help us to find the total number of saplings planted by Rahim.

The total number of saplings = (2x² + 5x − 7) rows × 3y² saplings in each row.

 = 3y² × (2x² + 5x − 7)

How do we find the product of the above algebraic expression?

Now,we will learn to find the product of algebraic expressions.

Note

Polynomial

A polynomial is an expression containing two or more algebraic terms. In a polynomial all variables are raised to only whole number powers.

a² + 2ab + b²

4x² + 3x – 7

A polynomial cannot contain :

1) Division by a variable. Eg. 4x² – (5/1+x) is not a polynomial.

2) Negative exponents. Eg. 7x^–2 + 5x – 6 is not a polynomial.

3) Fractional exponents. Eg. 3x³ + 4x^1/2 + 5 is not a polynomial.

Monomial

An expression which contains only one term is called a monomial. Examples:

4x, 3x² y, −2 y² .

Binomial

An expression which contains only two terms is called a binomial.

Examples: 2x + 3, 5y² + 9 y, a²b² + 2b

Trinomial

An expression which contains only three terms is called a trinomial.

Examples : 2a²b −8ab + b² , m² −n ² + 3