Identities

Identities

We have studied in the previous class about standard algebraic identities. An identity is an equation satisfied by any value that replaces its variable(s). Now, we shall recollect four known identities, which are,

(a + b)² ≡ a ² + 2ab + b²  

(a − b)² ≡ a² − 2ab + b²

(a² − b² ) ≡ (a + b)(a − b)

(x + a)(x + b) ≡ x² + (a + b)x + ab

Instead of the symbol ≡, we use = to represent an identity without any confusion.

Try these

Expand the following

(i) ( p + 2)² =  p² + 2(p) (2) + 2² =  p² + 4p + 4

(ii) (3 − a)² =  3² − 2(3) (a) + a² = 9 − 6a + a²

(iii) (6² − x² ) = (6 + x) (6 − x)

(iv) (a + b)² − (a − b)² = a² + 2ab + b² − (a² − 2ab + b²)

= a² + 2ab + b² − a² + 2ab − b²

= (1 − 1) a² + (2 + 2) ab + (+1 −1) b² = 4ab

(v) (a + b)² = (a + b) × (a + b)

(vi) (m + n)(m − n) = m² − n²

(vii) (m + 7)² = m² + 14m + 49

(xiii) (k² - 49) = (k+ 7 )(k - 7 )

(ix) m² − 6m + 9 = (m − 3)²

(x) (m − 10)(m + 5) = m² + (−10 + 5)m + (−10)(5) = m² − 5m − 50

Note

x =1 is the only solution for 7x + 3=10 whereas any value of x satisfies (x+2)² = x² + 4x + 4. So 7 x + 3=10 is an equation (x+2)² = x² + 4x + 4 is an identity. An identity is an equation but vice versa is not true.

Application of Identities

The identities give an alternative method of solving problems on multiplication of algebraic expressions and also of numbers.

Example 3.8

Find the value of (3a + 4c)² by using (a+b)² identity.

Solution:

Comparing (3a + 4c)² with (a + b)² , we have a = 3a,b = 4c

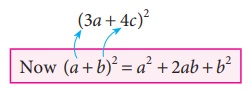
(3a + 4c)² = (3a )² + 2(3a)(4c ) + (4c)² (replacing a and b values)

= 3² a² + (2 × 3 × 4)(a × c) + 4² c²

(3a + 4c)² = 9a² + 24ac + 16c²

Example 3.9

Find the value of 998² by using (a−b)² identity.

Solution:

We know, 998 can be expressed as (1000 − 2)

(998)² = (1000 − 2)²

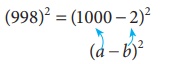
This is in the form of (a − b)² , we get a = 1000, b = 2

Now (a − b)² = a² − 2ab + b²

(1000 − 2)² = (1000)² − 2(1000)(2) + (2)²

(998)² = 1000000 − 4000 + 4 = 996004

Think

Which is corrcet? (3a)² is equal to

(i) 3a² (ii) 3²a (iii) 6a² (iv) 9a²

[Answer: (iv) 9a²]

Solution: (3a)² = 3²a² = 9a²

Example 3.10

Simplify (3x + 5y)(3x − 5 y) by using (a+b) (a−b) identity.

Solution:

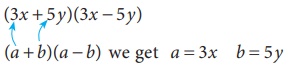
We have (3x + 5 y)(3x − 5 y)

Comparing it with (a + b)(a − b) we get a = 3x b = 5y

Now (a + b)(a − b) = a² − b²

(3x + 5y)(3x − 5y) = (3x)² − (5y)² (replacing a and b values)

= 3² x² − 5² y²

(3x + 5y)(3x − 5y) = 9x² − 25y²

Example 3.11

Expand y² −16 by using a²−b² identity

Solution:

y² −16 can be written as y² − 4²

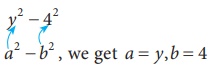
Comparing it with a² − b² , we get a = y,b = 4

Now a² − b² = (a + b)(a − b)

y² − 4² = ( y + 4)( y − 4)

y² − 16 = ( y + 4)( y − 4)

Example 3.12

Simplify (5x + 3)(5x + 4) by using (x+a) (x+b) identity.

Solution:

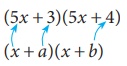
We have (5x + 3)(5x + 4)

Comparing it with (x + a)(x + b) , we get x = 5x and a = 3, b = 4

We know (x + a)(x + b) = x ² + (a + b)x + ab (replacing x, a and b values)

(5x + 3)(5x+4) = (5x)² + (3+4) (5x) + (3) (4)

 = 5² x ² + (7)(5x) + 12

(5x + 3)(5x + 4) = 25x ² + 35x + 12

Try these

Expand using appropriate identities.

(i) (3 p + 2q)²

(ii) (105)²

(iii) (2x − 5d)²

(iv) (98)²

(v) ( y − 5)( y + 5)

(vi) (3x)² − 5²

(vii) (2m + n)(2m + p)

(viii) 203 ×197

(ix) Find the area of the square whose side is (x − 2) units.

(x) Find the area of the rectangle whose length and breadth are ( y + 4) units and ( y − 3) units.

Solution:

1) (3p + 2q)²

Comparing (3p + 2q)² with (a + b)², we get a = 3p and b = 2q.

(a + b)² = a² + 2ab + b²

(3p + 2q)² = (3p)² + 2(3p) (2q) + (2q²) = 9p² + 12pq + 4q²

2) (105)² = (100+ 5)²

Comparing (100 + 5)² with (a + b)², we get a = 100 and b = 5.

(a + b)² = a² + 2ab + b²

(100 + 5)² = (100)² + 2 (100) (5) + 5² = 10000+ 1000 + 25

105² = 11,025

3. (2x − 5d)²

Comparing with (a – b)², we get a = 2x  b = 5d.

(a − b)² = a² − 2ab + b²

(2x − 5d)² = (2x)² − 2 (2x) (5d) + (5d)²

= 2²x² − 20xd + 5²d² = 4x² − 20xd + 25d²

4. (98)² = (100 − 2)²

Comparing (100− 2)² with (a − b)² we get

a = 100, b = 2

(a − b)² = a² − 2ab + b²

(100 − 2)² = 100² − 2 (100) (2) + 2²

= 10000 − 400 + 4 = 9600 + 4 = 9604

5. (y − 5) (y + 5)

Comparing (y − 5) (y + 5) with (a − b) (a + b) we get

a = y ; b = 5

(a − b) (a + b) = a² − b²

(y − 5)(y + 5) = y² − 5² = y² – 25

6. (3x)² − 5²

Comparing (3x)² − 5² with a² − b² we have

a = 3x ; b = 5

(a² − b²) = (a + b) (a − b)

(3x)² − 5² = (3x + 5) (3x − 5) = 3x (3x − 5) + 5 (3x − 5)

= (3x) (3x) − (3x) (5) + 5 (3x) − 5 (5)

= 9x² − 15x + 15x − 25 = 9x² – 25

7. (2m + n) (2m + p)

Comparing (2m + n) (2m + p) with (x + a) (x + b) we have

x = 2n ; a = n ; b = p

(x − a)(x + b) = x² + (a + b) x + ab

(2m + n) (2m + p) = (2m²) + (n + p)(2m) + (n) (p)

= 2²m² + n (2m) + p (2m) + np

= 4m² + 2mn + 2mp + np

8. 203 × 197 = (200 + 3) (200 − 3)

Comparing (a + b) (a − b) we have

a = 200, b = 3

(a + b) (a − b) =  a² − b²

(200 + 3) (200 − 3) = 200² − 3²

203 × 197 = 40000 − 9

203 × 197 = 39991

9. Side of a square = x − 2

∴ Area = Side × Side

= (x − 2) (x − 2) = x (x − 2) −2 (x − 2)

= x(x) + (x) (−2) + (−2)(x) + (−2) (−2)

= x² − 2x − 2x + 4

= x² − 4x + 4 units square

10. Length of the rectangle = y + 4

breadth of the rectangle = y − 3

Area of the rectangle = length × breadth

= (y + 4)(y − 3) = y² + (4 + (−3)) y + (4) (−3)

= y² + y – 12