Linear Graph

Linear Graph

1. Linear pattern

Plot the following points on a coordinateplane:(0,2),(1,3),(2,4),(3,5), (4, 6).What do you find? They all lie on a line! There is some pattern in them.

Look at the y- coordinate in each ordered pair: 2 = 0+2; 3 = 1+2; 4 = 2+2; 5 = 3+2; 6 = 4+2 In each pair, the y- coordinate is 2 more than the x- coordinate. The coordinates of each point have the same relationship between them. All the points plotted lie on a line!

In such a case, when all the points plotted lie on a line, we say ‘a linear pattern’ exists.

In this example, we found that in each ordered pair y value = x value +2.

Therefore the linear pattern above can be denoted by the algebraic equation y = x + 2. Such an equation is called a linear equation and the line graph for linear equation is called a linear graph.

Linear equations use one (or more) variables where one variable is dependent on the other(s).

The longer the distance we travel by a taxi, the more we have to pay. The distance travelled is an example of an independent variable. Being dependent on the distance, the taxi fare is called the dependent variable.

The more one uses electricity, greater will be the amount of electricity bill. The amount of electricity consumed is an example for independent variable and the bill amount is naturally the dependent variable.

2. Graph of a linear function in two variables

We have talked about parallel lines, intersecting lines etc., in geometry but never actually looked at how far apart they were, or where they were .Drawing graphs helps us place lines. A linear equation is an equation with two variables (like x and y) whose graph is a line. To graph a linear equation, we need to have at least two points, but it is usually safe to use more than two points. (Why?) When choosing points, it would be nice to include both positive and negative values as well as zero. There is a unique line passing through any pair of points.

Example 3.44

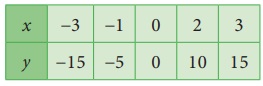
Draw the graph of y = 5 x

Solution:

The given equation y = 5 x means that for any value of x, y takes five times of x value.

Plot the point (−3,−15) (−1,−5) (0,0) (2,10) (3,15)

Example 3.45

Graph the equation y = x + 1.

Begin by choosing a couple of values for x and y. It will firstly help to see

(i) what happens to y when x is zero and

(ii) what happens to x when y is zero.

After this we can go on to find one or two more values.

Let us find at least two more ordered pairs. For easy graphing, let us avoid fractional answers.

We shall make suitable guesses.

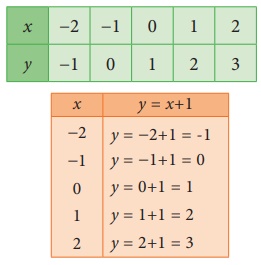
We have now five points of the graph: (−2,−1) (−1, 0) (0, 1) (1, 2) and (2, 3).

Note

The orientation of the graph will be different according to the scale chosen.

Try these

Identify and correct the errors

Solution: