Exercise 3.6 (Linear Equation in One Variable)

Exercise 3.6

1. Fill in the blanks

(i) The value of x in the equation x + 5 = 12 is --------------------

[Answer: 7]

Solution:

Given, x + 5 = 12

x = 12 − 5 = 7 (by transposition method)

Value of x is 7

(ii) The value of y in the equation y − 9 = ( −5) + 7 is --------------------

[Answer: 11]

Solution:

Given, y − 9 = (−5) + 7

y − 9 = 7 − 5 (re−arranging)

y − 9 = 2

∴ y = 2 + 9 = 11 (by transposition method)

(iii) The value of m in the equation 8m = 56 is--------------------

[Answer: 7]

Solution:

Given, 8m = 56

Divided by 8 on both sides

[ 8 × m ] / 8 =  56 / 8

∴  m = 7

(iv) The value of p in the equation 2p/3 = 10 is --------------------

[Answer: 15]

Solution:

Given, 2p / 3 = 10

Multiplying by 3 on both sides,

[2p / 3] × 3 = 10 × 3

Dividing by 2 on both sides

2p / 2  = 30 / 2

∴  p = 15

(v) The linear equation in one variable has -------------------- solution.

[Answer: one]

2. Say True or False.

(i) The shifting of a number from one side of an equation to other is called transposition. [Answer: True]

(ii) Linear equation in one variable has only one variable with power 2. [Answer: False]

[ correct statement : Linear equation in one variable has only one variable with power one ]

3. Match the following :

(a) x/2 = 10 : (i) x = 4

(b) 20= 6x – 4 : (ii) x = 1

(c) 2x – 5 = 3 – x : (iii) x = 20

(d) 7x – 4 – 8x = 20 : (iv) x = 8/3

(e) 4/11 − x = −7/11 : (v) x = –24

(A) (i), (ii), (iv), (iii), (v)

(B) (iii), (iv), (i), (ii), (v)

(C) (iii), (i), (iv), (v), (ii)

(D) (iii), (i), (v), (iv), (ii)

[Answer: (C) (iii), (i), (iv), (v), (ii)]

Solution:

a. x/2 = 10, multiplying by 2 on both sides, we get

[x / 2] × 2 = 10 × 2  ⇒ x = 20

b. 20 = 6x – 4 by transposition  ⇒ 20 + 4 = 6x

6x = 24 dividing by 6 on both sides,

6x / 6 = 24 / 6 ⇒ x = 4

c. 2x − 5 = 3 − x

By transposing the variable ‘x’, we get

2x − 5 + x = 3

by transposing − 5 to other side,

2x + x = 3 + 5

∴ 3x = 8 , 3x / 3 = 8 / 3

∴ x = 8 / 3

d. 7x − 4 − 8x = 20

by transposing − 4 to other side,

7x − 8x = 20 + 4

− x = 24

∴ x = − 24

e. 4/11 – x = −7 / 11

Transposing 4/11 to other side,

−x = [−7/11] [–4/11] =  [−7 – 4] / 11 = −11/11 = −1

∴ − x = − 1 ⇒ x = 1

4. Find x and p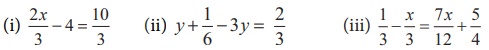 

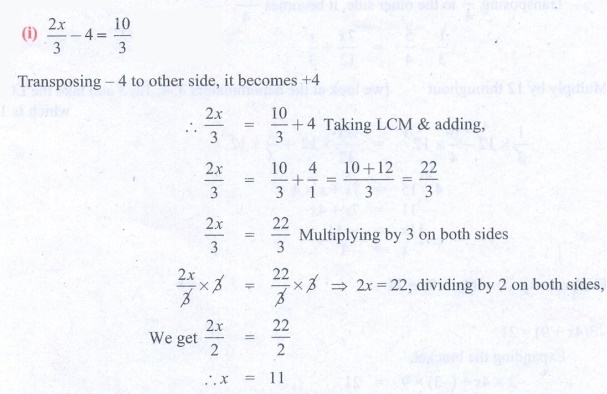
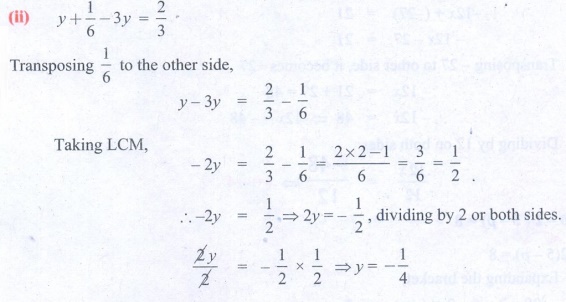
(i) 2x/3 − 4 = 10/3 (ii) y + 1/6 − 3y = 2/3 (iii) 1/3 – x/3 = 7x/12 + 5/4

(i) 2x/3 – 4 = 10/3

Solution:

Transposing − 4 to other side, it becomes + 4

∴ 2x / 3  = 10/3 + 4 Taking LCM & adding,

2x/3 = 10/3 + 4/1 =  [10 + 12] / 3 = 22 / 3

2x/3 = 22/3 Multiplying by 3 on both sides

[2x/3] × 3 = [22/3] × 3 ⇒ 2x = 22, dividing by 2 on both sides,

We get 2x / 2 = 22 / 2

∴ x = 11

(ii) y + 1/6 – 3y = 2/3

Solution:

Transposing 1/6 to other side,

y – 3y = 2/3 – 1/6

Taking LCM,

−2y = 2/3 – 1/6 = [2 × 2 – 1] / 6 = 3/6 = 1/2

∴  −2y  = 1/2  ⇒ 2y = −1/2, dividing by 2 or both sides.

2y / 2 = –1/2 × 1/2   ⇒ y = −1/4

(iii) 1/3 – x/3 = 7x/12 + 5/4

Transposing −x/3 to other side, it becomes + x/3

∴ 1/3 = 7x/12 + 5/4 + x/3

Transposing 5/4 to other side,  it becomes −5/4

1/3 – 5/4 = 7x/12 + x/3

Multiply by 12 throughout [we look at the denominators 3, 4, 12, 3 and take the LCM, which is 12]

[ (1/3) × 12 ] – [ (5/4) × 12 ] = [ 7x/12 × 12 ] + [ x/3 × 12 ]

4 − 15 = 7x + x × 4

−11 = 7x + 4x

11x = − 11

x = − 1

5. Find x (i) –3(4x + 9) = 21 (ii) 20 – 2 ( 5 – p) = 8 (iii) (7x – 5) – 4(2 + 5x) = 10(2 – x)

(i) −3(4x + 9) = 21

Solution:

− 3(4x + 9) = 21

Expanding the bracket,

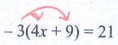
−3 × 4x + (−3) × 9 = 21

∴ −12x + (−27) = 21

−12x − 27 = 21

Transposing − 27 to other side, it becomes +27

− 12x = 21 + 27 = 48

∴ −12x = 48 ⇒  12x = − 48

Dividing by 12 on both sides

12x / 12 = − 48 / 12 ⇒  x = − 4

(ii) 20 − 2 ( 5 − p) = 8

Solution:

20 − 2(5 − p) = 8

Expanding the bracket,

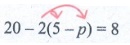
20 − 2 × 5 − 2 × (−p) = 8

20 − 10 + 2p = 8       ( −2 × –p = 2p)

10 + 2p = 8   transposing 10 to other side,

2p = 8 – 10 = − 2

∴  2p =  − 2  ∴  p = − 1

(iii) (7x − 5) − 4(2 + 5x) = 10(2 − x)

Solution:

(7x − 5) − 4(2 + 5x) = 10(2 − x)

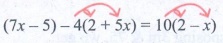
Expanding the brackets,

7x – 5 − 4 × 2 − 4 × 5x = 10 × 2 + 10 × (− x)

7x − 5 − 8 − 20x = 20 − 10x

7x – 13 − 20x = 20 − 10x

Transposing 10x & − 13, we get

7x − 13 − 20x + 10x = 20

7x − 20x + 10x = 20 +13, Simplifying,

−3x = 33

∴  3x = −33

x = −33 / 3 = − 11

x = −11 

6. Find x and m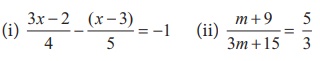 

(i) (3x−2)/4 − (x−3)/5 = −1 (ii) (m + 9) / (3m + 15) = 5/3

(i) [(3x – 2) / 4] – [(x − 3) / 5] = −1

Solution:

Taking LCM on LHS,

[ (3x − 2) × 5 − (x − 3) × 4 ] / 20 = −1

Expanding brackets,

[ 3x × 5 – 2 × 5 – x × 4 − (−3) × 4 ] / 20 = −1

[ 15x − 10 − 4x − (−12) ] / 20 = − 1

[ 15x − 10 − 4x +12 ] / 20 =  −1 ⇒ [ 11x + 2 ] / 20 = −l

Multiplying both sides by 20

[(11x + 2) / 20] × 20 = −l × 20

∴  11x  + 2 = − 20

∴ 11x  = − 20 – 2 = − 22

x  = −22/11 = − 2     

∴  Answer : x  = − 2

(ii) [ m + 9 ] / [ 3m + 15 ] = 5/3

Cross multiplying, we get

[m + 9 ] / [3m + 15]  cross over [5 / 3]

(m + 9) × 3 = 5 × (3m + 15)

m × 3 + 9 × 3 = 5 × 3m + 5 × 15

3m + 27 = 15m + 75    Transporting 3m & 75, we get

27 − 75 = 15m − 3m

−48 = 12m

12m / 12 =  − 48 / 12

⇒ m  = − 4

Answer:

Exercise 3.6

1. (i) x = 7 (ii) y = 11 (iii) m = 7 (iv) p = 15 (v) One

2. (i) True (ii) False

3. (c) (iii),(i), (iv), (v), (ii)

4. (i) x = 11 (ii) y = 1/-4 (iii) x = −1

5. (i) x = −4 (ii) p = −1 (iii) x = −11

6. (i) x = −2 (ii) m = −4