Multiplication of Algebraic Expressions

Multiplication of Algebraic Expressions

While doing the product of algebraic expressions, we should follow the steps given below.

Step 1: Multiply the signs of the terms. That is, the product of two like signs are positive and the product of two unlike signs are negative.

Step 2: Multiply the corresponding co-efficients of the terms.

Step 3: Multiply the variable factors by using laws of exponents.

If ‘x’ is a variable and m, n are positive integers then,

x ^m × xⁿ = x^{m +n}

For example, x³ × x⁴ = x^{3 +4} = x⁷

Think

Every algebraic expression is a polynomial. Is this statement true? Why?

Solution:

No, This statement is not true. Because Polynomials contain only whole numbers as the powers of their variables. But an algebraic expression may contains fractions and negative powers on their variables.

Eg. 2y² + 5y⁻¹ − 3 is a an algebraic expression. But not a polynomial.

A polynomial is a special kind of algebraic expression. The difference between an algebraic expression and a polynomial is,

Algebraic Expression

May contains whole numbers, fractions, negative numbers as the power of their variables.

Example: 4x^3/2 − 3x + 9

2 y² + 5/y − 3 , 3x² − 4x + 1

Polynomial

contains only whole numbers as the power of their variables.

Example: 4x ² − 3x + 9

2 y ⁶ + 5y³ − 3

Note

Product of two terms is represented by the symbols ( ), dot (.) or × .

For example,

multiplying 4x² and xy can be written in any one of the following ways.

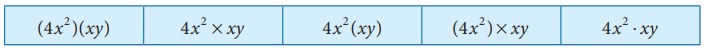
1. Multiplication of two or more monomials

Consider that, Geetha buys 3 pens each @ ₹5, how much she has to pay to the shopkeeper?

Geetha has to pay to the shopkeeper = 3 × ₹5

 = ₹15

If there are ‘x’ pens and the cost of each pen is ₹ ‘y’, then the cost of (3x² ) pens bought by Geetha @ ₹ 5y

@ - at the rate of

= (3x ² ) × 5y

= (3 × 5)(x ² × y)

= ₹ 15x²y

Example 3.1

If the length and breadth of a rectangular painting are 4xy³ and 3x ² y . Find its area.

Solution:

Area of the rectangular painting, A = (l × b) sq.units

= (4xy³ ) × (3x ² y)

= (4 × 3)(x × x² )( y ³ × y)

A = 12x ³ y⁴ sq.units

Example 3.2

Find the product of 2x ² y² , 3 y ²z and – z ² x³

Solution:

We have, (2x ² y² ) × (3 y ² z) × (−z ² x³ )

 = ( +) × ( +) × ( −)(2 × 3 ×1)(x ² × x³ )( y ² × y² )(z × z² )

= −6x ⁵ y⁴z³

Try these

Find the product of

(i) 3ab² , −2a²b³

(ii) 4xy, 5 y² x,(−x² )

(iii) 2m, −5n, −3p

Solution:

(i) (3ab²) × (−2a²b³) = (+) × (−) × (3 × 2) × (a × a²) × (b² × b³) = − 6a³ b⁵

(ii) (4xy) × (5y²x) × (−x²) = (+) × (+) × (−) × (4 × 5 × 1) × (x × x × x²) × (y × y²)

= −20 x⁴y³

(iii) (2m) × (−5n) × (−3p) = (+) × (−) × (−) × (2 × 5 × 3) × m × n × p

 = + 30 mnp = 30 mnp

2. Multiplication of a polynomial by a monomial

If there are ‘a’ shops and each shop has ‘x’ apples in 8 baskets and ‘y’ oranges in 3 baskets and ‘z’ bananas in 5 baskets, then the total number of apples, oranges and bananas are

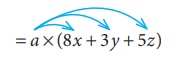
= a × (8x + 3y + 5z)

= a(8x) + a(3y) + a(5z)

(using distributive law).

 = 8ax + 3ay + 5az

monomial × monomial = monomial

binomial × monomial = binomial

binomial × binomial = binomial/polynomial

polynomial × monomial = polynomial

Note

Distributive law

If a is a constant, x and y are variables then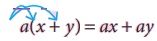 

 a(x + y) = ax + ay

For example, 5(x + y) = 5x + 5 y

Think

Why 3+(4x–7y) ≠ 12x−21y ?

Solution:

Addition and multiplication are different 3 + (4x − 7y) = 3 + 4x − 7y

We can add only like terms.

Example 3.3

Multiply 3x ² y and (2x ³ y³ − 5x ² y + 9xy)

Solution:

Now, (3x ² y) × (2x ³ y³ − 5x ² y + 9xy)

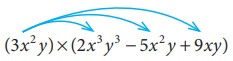
= 3x ² y(2x ³ y³ ) − 3x ² y (5x ² y ) + 3x ² y(9xy)

multiplying each term of the polynomial by the monomial

= (3 × 2)(x ² × x³ )( y × y³ ) − (3 × 5)(x ² × x² )( y × y) + (3 × 9)(x ² × x)( y × y)

= 6x⁵y⁴ − 15x⁴ y² + 27x ³ y²

Example 3.4

Ram deposited ‘x’ number of ₹2000 notes, ‘y’ number of ₹500 notes, ‘z’ number of ₹100 notes in a bank and Velan deposited ‘3xy’ times of amount of what Ram had deposited. How much amount did Velan deposit in the bank?

Solution:

Amount deposited by Ram

= ( x ×₹ 2000 + y ×₹ 500 + z ×₹100)

= ₹( 2000x + 500 y +100z )

Amount deposited by Velan = 3xy times × Amount deposited by Ram

 = ₹ 3xy × (2000x + 500 y + 100z)

 = (3 × 2000)(x × x × y ) + (3 × 500)(x × y × y ) + (3 ×100)(x × y × z)

 = ₹ (6000x ² y + 1500xy ² + 300xyz)

Try these

Multiply

(i) (5 x² + 7x – 3) by –4x²

(ii) (10x – 7y + 5z) by 6xyz

(ii) (ab+3bc –5ca) by 3a²bc

(iv) (4m² – 3m + 7) by –5m³

Solution:

(i) (5x² + 7x − 3) by – 4x²

(5x² + 7x − 3) × (– 4x²) = 5x² (− 4x²) + 7x (− 4x²) − 3(− 4x²)

= − 20 x⁴ − 28x³ + 12x²

(ii) (10x −7y + 5z) by 6xyz

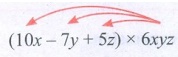
(10x −7y + 5z) × 6xyz = 6xyz (10x − 7y + 5z) [∵ Multiplication is commutative]

= 6xyz(10x) + 6xyz(−7y) + 6xyz(5z)

= (6 × 10) (x × x × y × z) + (6 × −7) + (x × y × y × z ) + (6 × 5)(x × y × z × z)

= 60x²yz + (−42xy²z) + 30xyz²

= 60x²yz − 42xy²z + 30xyz²

(iii) (ab + 3bc − 5ca) by 3a² bc

 (ab + 3bc − 5ca) × (3a²bc) = ab(3a²bc) + 3bc (3a²bc) − 5ca (3a²bc)

= 3a²b²c + 9a²b²c² − 15a³bc²

(iv) (4m² − 3m + 7) by − 5m³

 (4m² − 3m + 7) × (− 5m³) = 4m² (− 5m³) − (3m) (− 5m³) + 7(− 5m³)

= − 20m⁵ + 15m⁴ − 35m³

3. Multiplication of two binomials

Consider that a rectangular flower bed whose length is decreased by 5 units from the original length and whose breadth is increased by 3 units to the original breadth. What is the area of the rectangular flower bed?

Area of the rectangle = l × b

Here, area of the rectangular flower bed A = (l − 5) × (b + 3) sq.units

How do we multiply this?

Now, let us learn how to multiply two binomials

If (x + y) and ( p + q) are two binomials, we can find their product as given below,

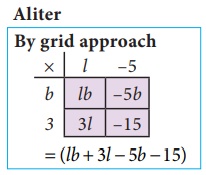
So, the above area of the rectangle = (l − 5) × (b + 3)

(By horizontal distributive approach) = l (b + 3) − 5(b + 3)

A = (lb + 3l − 5b −15) sq.u

Let us consider one more example. Consider the given figure , In the square OABC,

OA= 4 units ; OC =4 units

The area of the square OABC = 4 × 4

A = 16 sq.units

If the sides of the square are increased by ‘x’ units and ‘y’ units respectively,then we get the rectangle ODEF whose sides are OD=(4+x) units and OF=(4+y) units.

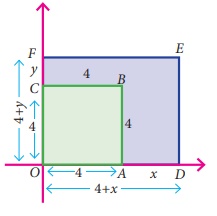
Now, the area of the rectangle ODEF = (4+x) (4+y) (by FOIL approach)

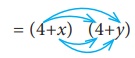
A = 16+ 4y + 4x + xy sq. units.

(all are unlike terms andso, we can’t add)

Example 3.5

Multiply (2x + 5 y) and (3x − 4 y)

Solution:

By horizontal distributive approach,

(2x + 5y) (3x − 4 y) = 2 x (x − 4 y) + 5 y ( x − 4 y)

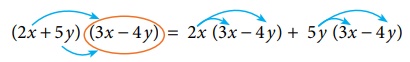
= 6x² − 8xy + 15xy − 20 y²

 = 6x² + 7xy − 20 y² (simplify the like terms)

Try these

Multiply

(i) (a − 5) and (a + 4)

(ii) (a + b) and (a − b)

(iii) (m⁴ + n⁴ ) and (m − n)

(iv) (2x + 3)(x + 4)

(v) (3x + 7)( x −5)

(vi) (x − 2)(6x − 3)

Solution:

(i) (a − 5) and (a + 4)

 (a − 5) (a + 4) = a(a + 4) − 5(a + 4)

= (a × a) + (a × 4) + (−5 × a) + (−5 × 4)

= a² + 4a − 5a − 20 = a² − a − 20

(ii) (a + b) and (a − b)

 (a + b) (a − b) = a(a − b) + b(a − b)

= (a × a) + (a × −b) + (b × a ) + b(− b)

= a² − ab + ab − b² = a² − b²

(iii) (m⁴ + n⁴) and (m − n)

(m⁴ + n⁴) (m − n) = m⁴ (m − n) + n⁴ (m − n)

= (m⁴ × m) + (m⁴ × (− n)) + (n⁴ × m) + (n⁴ × (−n))

= m⁵ − m⁴ n + mn⁴ – n⁵

(iv) (2x + 3) (x + 4)

 (2x + 3) (x + 4)  = 2x(x + 4) + 3(x + 4)

= (2x² × x) + (2x × 4) + (3 × x) + (3 × 4)

= 2x² + 8x + 3x + 12 = 2x² + 11x + 12 

(v) (3x + 7) (x − 5)

 (3x + 7) (x − 5)  = x(3x + 7) − 5(3x + 7)

= (x × 3x) + (x × 7) + (−5 × 3x) + (−5 × 7)

= 3x² + 7x − 15x − 35

= 3x² − 8x – 35

(vi) (x − 2) (6x − 3)

 (x − 2) (6x − 3)  = x(6x − 3) − 2(6x − 3)

= (x × 6x) + (x × (−3) − (2 × 6x) − (2 × 3)

= 6x² − 3x − 12x + 6

= 6x² − 15x + 6

Think

(i) In 3x² (x⁴–7x³+2), what is the highest power in the expression?

Solution:

3x² (x⁴ − 7x³ + 2)  = (3x²) (x⁴) + 3x² (− 7x³) +  (3x²)2

= 3x²  − 21x⁵ + 6x²

Highest power is 6 in x⁶.

(ii) Is –5y² +2y–6 = –(5y² +2y–6)? If not, correct the mistake.

Solution:

No, – 5y² + 2y – 6 = − (5y² − 2y + 6 )