Linear Equation in One Variable

Linear Equation in One Variable

1. Introduction

We shall recall some earlier ideas in algebra.

What is the formula to find the perimeter of a rectangle? If we denote the length by l and breadth by b, the perimeter P is given as P = 2(l + b). In this formula, 2 is a fixed number whereas the literal numbers P, l and b are not fixed because they depend upon the size of the rectangle and hence P, l and b are variables. For rectangles of different sizes, their values go on changing. 2 is a constant (which does not change whatever may be the size of the rectangle).

An algebraic expression is a mathematical phrase having one or more algebraic terms including variables, constants and operating symbols (such as plus and minus signs).

Example: 4x² + 5x + 7xy + 100 is an algebraic expression; note that the first term 4x² consists of constant 4 and variable x². What is the constant in the term 7xy? Is there a variable in the last term of the expression?

The ‘number parts’ of the terms with variables are coefficients. In 4x² + 5x + 7xy + 100, the coefficient of the first term is 4. What is the coefficient of the second term? It is 5. The coefficient of the xy term is 7.

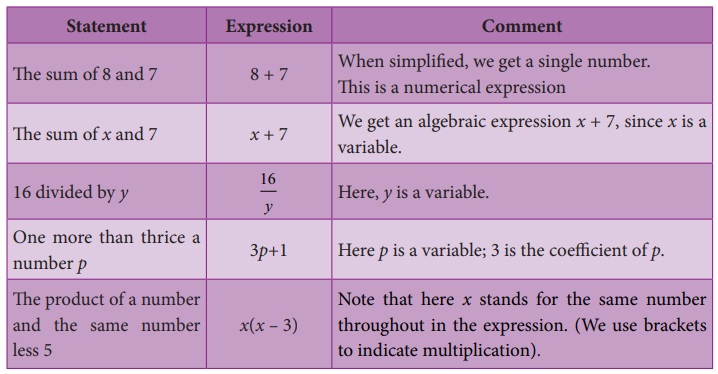
2. Forming algebraic expressions

We now to translate a few statements into an algebraic language and recall how to frame expressions. Here are some examples:

3. Equations

An equation is a statement that asserts the equality of two expressions; the expressions are written one on each side of an “equal to” sign.

For example: 2x + 7 = 17 is an equation (where x is a variable). 2x + 7 forms the Left Hand Side (LHS) of the equation and 17 is its Right Hand Side (RHS).

Linear equations

An equation containing only one variable with its highest power as one is called a linear equation. Examples: 3x – 7 = 10.

Linear equations in one or more variables:

An equation is formed when a statement is put in the form of mathematical terms.

Here are some examples:

(i) A number is added to 5 to get 25

This statement can be written as x + 5 = 25.

This equation x + 5 = 25 is formed by one variable (x) whose highest power is 1. So it is called a linear equation in one variable.

Therefore, an equation containing only one variable with its highest power as one is called a linear equation in one variable.

Examples: 5x − 2 = 8, 3y + 24 = 0

This linear equation in one variable is also known as simple equation.

(ii) Sum of two numbers is 45

This statement can be written as x + y = 45.

This equation x + y = 45 is formed by two variables x and y whose highest power is 1. Hence, we call it as a linear equation in two variables.

Now, in this class we shall learn to solve linear equations in one variable only. You will learn to solve other type of equations in higher classes.

Note

The equations so formed with power more than 1 of its variables, (2,3....etc.) are called as quadratic, cubic equations and so on.

Examples: (i) x² + 4x + 7 = 0 is a quadratic equation.

(ii) 5 x³ − x² + 3x = 10 is a cubic equation.

Try these

Identify which among the following are linear equations.

(i) 2 + x = 19 − Linear as degree of the variable x is 1

(ii) 7x² – 5 = 3 − not linear as highest degree of x is 2

(iii) 4p³ = 12 − not linear as highest degree of p is 3

(iv) 6m+2 − Linear, but not an equation

(v) n=10 −  Linear equation as degree of n is 1

(vi) 7k – 12= 0 − Linear equation as degree of k is 1

(vii) 6x/8 + y = 1 − Linear equation as degree of x & y is 1

(viii) 5 + y = 3x − Linear equation as degree of y & x is 1

(ix) 10p+2q=3 − Linear equation as degree of p & q is 1

(x) x²–2x–4 − not linear equation as highest degree of x is 2

Convert the following statements into linear equations:

Example 3.28

7 is added to a given number to give 19.

Solution:

Let the number be n.

When 7 is added to this number we get n + 7.

This result is to give 19.

Therefore, the equation is n + 7 = 19.

Think

(i) Is t(t – 5)=10 a linear e quation? Why?

Solution:

t(t − 5) = 10

= (t × t) – (5 × t) = 10

= t² − 5t = 10

This is not a linear equation as the highest degree of the variable ‘t’ is 2 

(ii) Is x² =2x , a linear equation? Why?

Solution:

x² = 2x

= x² − 2x = 0

This is not a linear equations as the highest degree of the variable ‘x’ is 2

Example 3.29

The sum of 4 times a number and 18 is 28.

Solution:

Let the number be x.

4 times the number is 4x.

Adding 18 now, we get 18 + 4x.

Now the result should be 28.

Thus, the equation has to be 18 + 4x = 28.

Try these

Convert the following statements into linear equations:

• On subtracting 8 from the product of 5 and a number, I get 32.

Solution:

Convert to linear equations:

Given that on subtracting 8 from product of 5 and a, we get 32

∴  5 × x − 8 = 32

∴  5x − 8 = 32

• The sum of three consecutive integers is 78.

Solution:

Sum of 3 consecutive integers is 78

Let 1^st integer be ‘x’

∴  x + (x + 1) + (x + 2) = 78

∴  x + x + l + x + 2 = 78

3x + 3 = 78 

• Peter had a Two hundred rupee note. After buying 7 copies of a book he was left with ₹60.

Solution:

Let cost of one book be ‘x’

∴ Given that 200 −7 × x = 60

∴ 200 − 7x = 60

• The base angles of an isosceles triangle are equal and the vertex angle measures 80°.

Solution:

Let base angles each be equal to x & vertex bottom angle is 80°. Applying triangle property, sum of all angles is 180°

∴  x + x + 80 = 180°

∴  2x + 80 = 180

• In a triangle ABC, ∠A is 10^o more than ∠B. Also ∠C is three times ∠A. Express the equation in terms of angle B.

Solution:

Let ∠B  = b

Given ∠A = 10° + ∠B = 10 + b

Also given that ∠C = 3 × ∠A = 3 × (10 + b) = 30 + 3b

Sum of the angles = 180°

∠A + ∠B + ∠C = 180°

10 + b + b + 30 + 3b = 180°

∴  5b + 40 = 180°

4. Solution of a linear equation

The value which replaces a variable in an equation so as to make the two sides of the equation equal is called a solution or root of the equation.

Example : 2 x = 10

We find that the equation is “satisfied” with the value x = 5. That is, if we put x = 5, in the equation, the value of the LHS will be equal to the RHS. Thus x = 5 is a solution of the equation. Note that no other value for x satisfies the equation. Thus one can say x = 5 is “the” solution of the equation.

(i) The DO-UNDO Method:

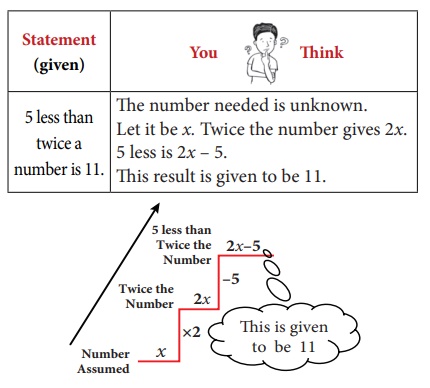
This formation of equation can be visualized as follows:

From the number x, we reached 2x – 5 by performing operations like subtraction, multiplication etc. So when 2x – 5 = 11 is given, to get back to the value of x, we have to 'undo' all that we did! Thus, we ‘do’ to form the equation and ‘undo’ to get the solution.

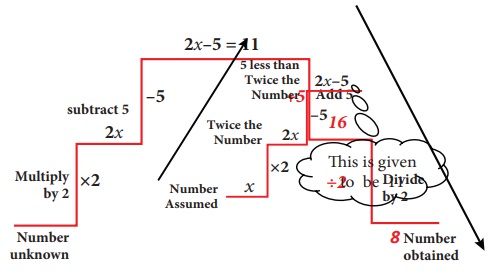
Example 3.30

(a) Solve the equation: x − 7 = 6

Solution:

 x – 7 = 6 (Given)

 x – 7 +7 = 6+7 (add 7 on both sides)

 x = 13

(b) Solve the equation: 3x = 51

Solution:

3x = 51 (Given)

3 × x = 51

3/3 × x/3 = 51/3 (÷ 3 on both sides)

x = 17

(ii) Transposition method

The shift ing of a number from one side of an equation to other is called transposition.

For the above example, (a) doing addition of 7 on both sides is the same as changing the number –7 on the left hand side to its additive inverse +7 and add it on the right hand side.

 x – 7 = 6

 x = 6+7

 x = 13

Think

Can you get more than one solution for a linear equation?

Solution:

Yes, we can get. Consider the below line or equation

x + y = 5

here, when x = 1, y = 4

when x = 2, y = 3

x = 3, y = 2

x = 4, y = 1

Hence, we get multiple solutions for the same linear equation.

likewise, (b) doing division by 3 on both sides is the same as changing the number 3 on the LHS to its reciprocal 1/3 and multiply it on the RHS and vice-versa.

 For Example

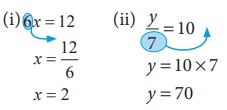
Note

While rearranging the given linear equation, group the like terms on one side of the equality sign, and then do the basic arithmetic operations according to the signs that occur in the expression.

Try these

1. Solve for ‘x’ and ‘y’

 (i) 2x = 10

(ii) 3 + x = 5

(iii) x – 6 = 10

(iv) 3x + 5 = 2

 (v) 2x/7 = 3

(vi) –2 = 4m – 6

(vii) 4(3x – 1) = 80

(viii) 3x – 8 = 7 – 2x

(ix) 7 – y = 3(5 – y)

(x) 4(1 – 2y)–2(3 – y) = 0

Solution:

(i) 2x = 10

 ⇒ x = 10 / 2 = 5

(ii) 3 + x = 5

⇒ 3 + x = 5

x = 5 – 3 = 2

(iii) x − 6 = 10

⇒ x − 6 = 10

x = 10 + 6 = 16

(iv) 3x + 5 = 2

⇒ 3x + 5 = 2

3x = 2 – 5 = − 3

x = −3/3 = −1

(v) 2x/7  = 3

⇒ 2x = 3 × 7 = 21

x = 21/2

(vi) − 2x = 4m − 6

⇒ − 2x = 4m − 6

−2 + 6 = 4m

4 = 4m

m = 4 / 4 = 1

(vii) 4(3x − 1) = 80

⇒ 4(3x − l) = 80

12x − 4 = 80

12x = 80 + 4 = 84

x = 84 / 12 = 7

(viii) 3x − 8 = 7 − 2x

⇒ 3x − 8 =  7 − 2x

3x + 2x = 7 + 8 = 15

5x = 15

x = 15/5 = 3

(ix) 7 − y = 2(5 − y)

⇒ 7 − y = 3(5 − y)

7 − y = 15 − 3y

3y − y = 15 − 7

2y = 8

y = 8 / 2 = 4

(x) 4(l − 2y) − 2(3 −y) = 0

⇒ 4(1− 2y) – 2(3 − y) = 0

4 − 8y − 6 – 2y = 0

−2 − 6y = 0

6y = − 2

y = − 2 / 6 =  −1 / 3

Think

1. “An equation is multiplied or divided by a non zero number on either side.” Will there be any change in the solution?

Solution:

Not be any change in the solution

2. “An equation is multiplied or divided by two different numbers on either side”. What will happen to the equation?

Solution:

When an equation is multiplied or divided by 2 different numbers on either side, there will be a change in the equation & accordingly, solution will also change.