Exercise 3.3 (Cubic Identities)

Exercise 3.3

1. Expand

(i) (3m + 5)²

(ii) (5p −1)²

(iii) (2n − 1)(2n + 3)

(iv) 4 p ² − 25q²

Solution:

(i) (3m + 5)²

Comparing (3m + 5)² with (a + b)² we have a = 3m and b = 5

(a + b)² = a² + 2ab + b²

(3m + 5)² = (3m)² + 2 (3m) (5) + 5²

= 3² m² + 30 m + 25 = 9m² + 30m + 25

(ii) (5p − 1)²

Comparing (5p − l)² with (a − b)² we have a = 5p and b = 1

(a − b)² = a² − 2ab + b²

(5p − l)² = (5p)² − 2 (5p) (l) + l²

= 5²p² − 10p + 1 = 25p² − 10p + 1

(iii) (2n − 1) (2n + 3)

Comparing (2n − 1) (2n + 3) with (x + a) (x + b) we have a = − l; b = 3

(x + a) (x + b)  = x² + (a + b)x + ab

(2n + (− 1)) (2n + 3) = (2n)² + (−1 + 3) 2n + (−1) (3)

= 2²n² + 2 (2n) − 3= 4n² + 4n − 3

(iv) 4p² − 25q² = (2p)² − (5q)²

Comparing (2p)² − (5q)² with a² − b² we have a = 2p and b = 5q

(a² − b²) = (a + b) (a − b) = (2p + 5q) (2p − 5q)

2. Expand

(i) (3 + m)³

(ii) (2a + 5)³

(iii) (3 p + 4q)³

(iv) (52)³

(v) (104)³

Solution:

(i) (3 + m)³

Comparing (3 + m)³ with (a + b)³ we have a = 3 ;  b = m

(a + b)³ = a² + 3a²b + 3ab² + b³

(3 + m)³ = 3³ + 3(3)²(m) + 3(3) m² + m³

= 27 + 27m + 9m² + m³ = m³ + 9m² + 27m +  27

(ii) (2a + 5)³

Comparing (2a + 5)³ with (a + b)³ we have a = 2a, b = 5

(a + b)³ = a³ + 3a²b + 3ab² + b³

= (2a)³ + 3(2a)² 5 + 3 (2a) 5² + 5³

= 2³a³ + 3(2²a²) 5 + 6a (25) + 125

= 8 a³ + 60 a² + 150a + 125

(iii) (3p + 4q)³

Comparing (3p + 4q)³ with (a + b)³ we have a = 3p and b = 4q

(a + b) = a³ + 3a²b + 3ab² + b²

(3p + 4q)³  = (3p)³+ 3(3p)² (4q) + 3(3p) (4q)² + (4q)³

= 3³p³ + 3 (9p²) (4q) + 9p (16q²) + 4³q³

= 27p³ + 108p²q + 144pq² + 64q³

(iv) (52)³ = (50+ 2)³

Comparing (50 + 2)³ with (a + b)³ we have a = 50 and b = 2

(a + b)³ = a³ + 3a²b + 3ab² + b³

(50 + 2)³ = 50³ + 3 (50)² 2 + 3 (50)(2)² + 2³

52³ = 125000 + 6(2,500) + 150(4) + 8

= 1,25,000 + 15,000 + 600 + 8

52³ = 1,40,608

(v) (104)³ = (100+ 4)³

Comparing (100 + 4)³ with (a + b)³ we have a = 100 and b = 4

(a + b)³ = a³ + 3a²b + 3ab² + b³

(100 + 4)³ = (100)³ + 3 (100)² (4) + 3 (100) (4)² + 4³

= 10,00,000 + 3 (10000) 4 + 300 (16) + 64

= 10,00,000 + 1,20,000 + 4,800 + 64 = 11,24,864

3. Expand

(i) (5 − x)³

(ii) (2x − 4 y)³

(iii) (ab − c)³

(iv) (48)³

(v) (97xy)³

Solution:

(i) (5 − x)³

Comparing (5 − x)³ with (a − b)³ we have a = 5 and b = x

(a − b)³ = a³ − 3a²b + 3ab² − b³

(5 − x)³ = 5³ − 3 (5)² (x) + 3(5)(x²) − x³

= 125 − 3(25)(x) + 15x² − x³ = 125 − 75x + 15 x² − x³

(ii) (2x − 4y)³

Comparing (2x − 4y)³ with (a − b)³ we have a = 2x and b = 4y

(a − b)³ = a³ − 3a²b + 3ab² − b³

(2x − 4y)³ = (2x)³ − 3(2x)² (4y) + 3(2x) (4y)² − (4y)³

= 2³ x³ − 3(2² x²) (4y) + 3(2x) (4² y²) − (4³y³)

= 8x³ − 48x²y + 96xy² − 64y³

(iii) (ab − c)³

Comparing (ab − c)³ with (a − b)³ we have a = ab and b = c

(a − b)³ = a³ − 3a²b + 3ab² − b³

(ab − c)³ = (ab)³ − 3(ab)² c + 3ab (c)² − c³

= a³b³ − 3(a²b²) c + 3abc² − c³

= a³b³ − 3a²b² c + 3abc² − c³

(iv) (48)³ = (50 −2)³

Comparing (50 − 2)³ with (a − b)³ we have a = 50 and b = 2

(a − b)³ = a³ − 3a²b + 3ab² − b³

(50 − 2)³ = (50)³ − 3(50)² (2) + 3 (50)(2)² − 2³

= 1,25,000 − 15000 + 600 − 8 = 1,10,000 + 592

= 1,10,592

(v) (97xy)³

(97xy)³ = 97³ x³y³ = (100 − 3)³ x³y³ ... (1)

Comparing (100 − 3)³ with (a − b)³ we have a = 100, b = 3

(a – b)³ = a³ − 3a²b + 3ab² − b³

(100 − 3)³ = (100)³ − 3(100)² (3) + 3 (100)(3)² − 3³

97³ = 10,00,000 − 90000 + 2700 − 27

97³ = 910000 + 2673

97³ = 912673

97x³y³ = 912673x³y³

4. Simplify ( p − 2)( p + 1)( p − 4)

Solution:

(p − 2)(p + 1) (p − 4) = (p + (−2)) (p + l) (p + (−4))

Comparing (p − 2) (p + 1) (p − 4) with (x + a) (x + b) (x + c) we have x = p ; a = −2; b = 1 ; c = −4.

(x + a) (x + b) (x + c) = x² + (a + b + c) x² + (ab + bc + ca) x + abc

= p³ + (−2 + 1 + (−4)) p² + ((−2) (1) + (1) (−4) + (−4) (−2))p + (−2) (1) (−4)

= p³ + (−5) p² + (−2 + (−4) + 8) p + 8

= p³ − 5p² + 2p + 8

5. Find the volume of the cube whose side is (x +1) cm

Solution:

Given side of the cube = (x + 1) cm

Volume of the cube = (side)³ cubic units = (x + 1)³ cm³

We have (a + b)³ = (a³ + 3a²b + 3ab² + b³) cm³

(x + 1)³ = (x³ + 3x² (1) + 3x (1)² + l³) cm³

Volume = (x³ + 3x² + 3x + 1) cm³

6. Find the volume of the cuboid whose dimensions are (x + 2),(x −1) and (x − 3)

Solution:

Given the dimensions of the cuboid as  = (x + 2), (x – 1) and (x – 3)

∴ Volume of the cuboid = (l × b × h) units³

= (x + 2) (x − 1) (x − 3) units³

We have (x + a) (x + b) (x + c) = x³ + (a + b + c) x² + (ab + bc+ ca)x + abc

∴ (x + 2) (x − l) (x − 3) = x³ + (2 − 1 − 3)x² + (2 (−1) + (−1) (−3) + (−3) (2)) x +(2)(−l) (−3)

= x³ – 2x² + (−2 + 3 − 6)x + 6

Volume = x³ – 2x² − 5x + 6 units³

Objective Type Questions

7. If x²–y² = 16 and (x+y) = 8 then (x–y) is ___________

(A) 8

(B) 3

(C) 2

(D) 1

[Answer: (C) 2]

Solution:

x²− y² = 16

(x − y) (x − y) = 16

8 (x − y) = 16

(x − y) = 16 / 8 = 2

8. 

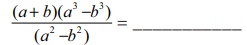
 (A) a²–ab+b²

(B) a²+ab+b²

(C) a²+2ab+b²

(D) a²–2ab+b²

[Answer: (B) a² + ab + b² ]

Solution:

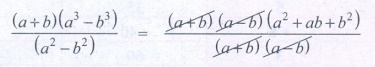
[(a − b)² (a³ – b³) ] / [(a² – b²)] =  [ (a + b) (a – b) a² + ab + b² )] / [ (a + b) (a – b)]

 = a² + ab + b²

9. (p+q)(p²–pq+q²) is equal to _____________

(A) p³+q³

(B) (p+q)³

(C) p³–q³

(D) (p–q)³

[Answer: (A) p³ + q³ ]

Solution:

a³ + b³  = (a + b)(a² − ab + b²)

10. (a–b)=3 and ab=5 then a³–b³ = ____________

(A) 15

(B) 18

(C) 62

(D) 72

[Answer: (D) 72]

Solution:

(a − b) = 3

(a − b)² = 3²

a² + b² − 2ab  = 9

a² + b² – 2(5)  = 9

a² + b² = 9 + 10

a² + b² = 19

a³ + b³ = (a – b) (a² + ab + b²) = 3 (19 + 5)

= 3(24) = 72

11. a³+b³ = (a+b)³ – __________

(A) 3a(a+b)

(B) 3ab(a–b)

(C) –3ab(a+b)

(D) 3ab(a+b)

[Answer: 3ab (a + b)]

Solution:

(a + b)³ = a³ + b³ + 3a²b + 3ab²

(a + b)³ – 3a²b − 3ab² = a³ + b³

(a + b)³ – 3ab (a + b)= a³ + b³

Answer

Exercise 3.3

1. (i) 9m² + 30 m + 25  (ii) 25 p² − 10p +1  (iii ) 4n² + 4n − 3 (iv) ( 2p + 5q )( 2p − 5q)

2. (i) m³ + 9m² + 27 m + 27 (ii) 8a³ + 60 a² +150 a +125 (iii ) 27 p³ + 108 p²q +144 pq² + 64q³ (iv) 14,0608 (v) 1124864

3. (i) 125 − 75 x +15x² − x³ (ii) 8x³ − 48x² y + 96 xy² − 64y³ (iii ) a³b³ − 3a²b²c + 3abc³ − c³

(iv) 110, 592 ( v ) 912673x³y³

4. p³ − 5p² + 2p + 8

5. x³ + 3x² + 3 x +1

6. x³ − 2x² − 5 x + 6

7. (C) 2 

8. (B) a² + ab + b²

9. (A) p³ + q³  

10. (D) 72

11. (D) 3ab(a+b)