Factorisation

Factorisation

Expressing any number as the product of two or more numbers is called as factorisation. The number 12 can be expressed as the product of prime factors like 12 = 2 × 2 × 3. This is called prime factorisation. How will you factorise an algebraic expression? Yes. Expressing an algebraic expression as the product of two or more expressions is called the Factorisation.

Note

A number which is divisible by 1 and itself (or) A number which has only 2 factors are called prime numbers. Example: 2, 3, 5, 7, 11, ...

A number which has more than 2 factors are called composite numbers.Example: 4, 6, 8, 9, 10, 12, ...

For example, (i) a ² − b² = (a + b)(a − b) Here, (a + b) and (a − b) are the two factors of a ² − b²

(ii) 5y + 30 = 5( y + 6) , Here 5 and ( y + 6) are the factors of 5y + 30

Any expression can be Factorised as (1) × (expression)

For example, a² − b² can also be factorised as

 (1) × ( a ² − b² ) or ( −1) × (b² − a² )

because ‘1’ is a factor for all numbers and expressions

So, when we factorise the expressions, follow the suitable type of factorisation given below to get two or more factors other than 1. Stop doing the factorisation process once you have taken out all the common factors from the expression and then list out the factors.

Type 1: Factorisation by taking out the common factor from each term.

Type 2 : Factorisation by taking out the common binomial factor from each term

Type 3 : Factorisation by grouping

Type 4 : Factorisation using identities

Type 5 : Factorisation of the expression (ax2 + bx + c)

Type 1: Factorisation by taking out the common factor from each term.

Example 3.18

Factorise: 4x ² y + 8xy

Solution:

We have, 4x ² y + 8xy This can be written as,

 = (2 × 2 × x × x × y ) + (2 × 2 × 2 × x × y)

Taking out the common factor 2, 2, x , y , we get

 = 2 × 2 × x × y(x + 2)

 = 4xy(x + 2)

Type 2 : Factorisation by taking out the common binomial factor from each term

Example 3.19

(i) Factorise: (2x + 5)(x − y ) + (4 y)(x − y)

Solution:

We have (2x + 5)(x − y ) + (4 y)(x − y)

Taking out the common binomial factor (x − y)

We get, (x − y)( 2x + 5 + 4 y)

(ii) Factorise 3n( p − 2) + 4(2 − p)

Solution:

We have 3n( p − 2) + 4(2 − p) (taking – as common)

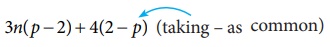
3n( p − 2) − 4( p − 2)

Taking out the common binomial factor ( p − 2)

We get, ( p − 2)(3n − 4)

Type 3 : Factorisation by grouping

Sometimes, the terms of a given expression are grouped suitably in such a way that they have a common factor so that the factorisation is easy to take out common factor from those terms.

Example 3.20

Factorise : x² + yz + xy + xz

Solution:

We have, x² + yz + xy + xz

Group the terms suitably as,

= ( x ² + xy ) + ( yz + xz)

= x (x + y ) + z( y + x)

= x (x + y ) + z(x + y) (addition is commutative)

= (x + y)[ x + z] [taking out the common factor (x + y) ]

Type 4 : Factorisation using identities

(i) (a + b)² = a ² + 2ab + b²

(ii) (a − b)² = a ² − 2ab + b²

(iii) a ² − b² = (a + b)(a − b)

Example 3.21

Factorise : x ² + 8x +16

Solution:

Now, x ² + 8x +16 can be written as x ² + 8x + 4²

Comparing this with a ² + 2ab + b² = (a + b)² we get a = x ; b = 4

(x²) + 2(x)(4) + (4)² = ( x + 4)²

x ² + 8x + 16 = ( x + 4)²

(x+4), (x+4) are the two factors.

Example 3.22

Factorise 49x ² − 84xy + 36 y²

Solution:

Now, 49x ² − 84xy + 36 y²

7² x² − 84xy + 6² y² = (7x)² − 84xy + (6 y)²

Comparing this with a² − 2ab + b² = (a − b)² we get a = 7x , b = 6 y

(7x)² − 2(7x)(6 y) + (6 y)² = (7x − 6 y)²

∴ 49x² − 84xy + 36 y²= (7x − 6 y)²

(7x–6y), (7x–6y) are the two factors.

Try these

Find the factors

Example 3.23

Factorise : 49x² − 64 y²

Solution:

Now, 49x² − 64 y²

7² x² − 8² y² = (7x)² − (8y)²

Comparing this with a² − b² = (a + b)(a − b) we get a = 7x , b = 8y

(7x)² − (8 y)² = (7x + 8 y)(7x − 8 y)

(7x+8y), (7x–8y) are the two factors.

Type 5 : Factorisation of the expression (ax² + bx + c)

Example 3.24

Factorise x²+ 8x+15

Solution:

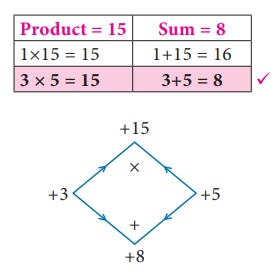
Given x² + 8x +15

This is in the form of ax² + bx + c

We get a = 1,b = 8, c = 15

Now, the product = a × c and sum = b b = 8

=1×15

= 15

= x² + 8x +15

= x² + 3x + 5x + 15 (the middle term 8x can be written as 3x+5x)

= (x² + 3x) + (5x +15)

= x(x + 3) + 5(x + 3) taking out the common factor x+3 )

 x² + 8x + 15 = ( x + 3)(x + 5)

Therefore, (x+3), (x+5) are the two factors.

Think

 x²–4(x–2) = (x²–4)(x–2)

Is this correct? If not correct it.

Solution:

Not correct

(3a)² = 3²a² − 9a²

x² − 4(x − 2) = x² – 4x + 8 

Example 3.25

Factorise 7c² + 2c – 5

Solution:

Given

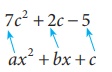
This is in the form of ax² + bx + c

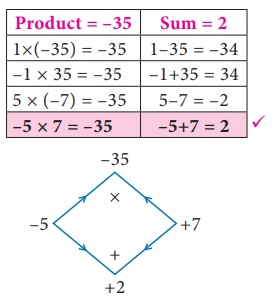
We get a = 7, b = 2, c = −5

Now, the product = a × c = 7 × (−5) = –35 and sum b = 2

= 7c ² + 2c – 5

= 7c ² – 5c + 7c – 5 (the middle term 2c can be written as –5c+7c)

= (7c ² − 5c) + (7c − 5)

= c (7c − 5) + 1(7c − 5) (taking out the common factor 7c–5 )

= (7c − 5)(c + 1)

Therefore, (7c–5), (c+1) are the two factors.

Try these

Factorise the following :

1) 3y + 6 

2) 10x ² +15y² 

3) 7m(m − 5) + 1(5 − m) 

4) 64 − x² 

5) x²–3x+2 

6) y²–4y–32 

7) p²+2p–15 

8) m²+14m+48 

9) x²–x–90 

10) 9x²–6x–8

Solution:

1. 3y + 6

3y + 6 = 3 × y + 2 × 3

Taking out the common factor 3 from each term we get 3 (y + 2)

∴ 3y + 6 = 3(y + 2)

2. 10x² + 15y²

10x² + 15y² = (2 × 5 × x × x) + (3 × 5 × y × y)

Taking out the common factor 5 we have

10x² + 15y²  = 5(2x² + 3y²)

3. 7m (m − 5) + (15 – m)

7m (m − 5) + (15 – m) = 7 m (m − 5) + (−1 )(−5 + m)

= 7m (m − 5) − 1(m − 5)

Taking out the common binomial factor (m − 5) = (m − 5) (7 m − 1)

4. 64 − x²

64 − x² = 8² − x²

This is of the form a² − b²

Comparing with a² − b² we have a = 8, b = x

a²− b² = (a + b) (a − b)

64 − x² = (8 + x) (8 − x)

5. x² – 3x + 2

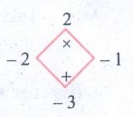
x² – 3x + 2 = x² − 2x − x + 2

= x (x − 2) − (x − 2)

= (x − 2) (x − l)

6. y² – 4y – 32

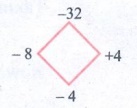
 y² – 4y – 32 = y² – 8y + 4y − 32

= y(y − 8) + 4(y − 8)

= (y − 8) (y + 4)

7. p² + 2p – 15

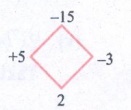
p² + 2p – 15 =  p² + 5p −3p − 15

= p(p + 5) −3 (p + 5)

= (p + 5) (p − 3)

8. m² + 14 m + 48

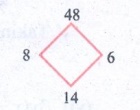
m² + 14 m + 48 = m² + 8 m + 6 m + 48

= m (m + 8) + 6 (m + 8)

= (m + 6) (m + 8)

9. x² − x – 90

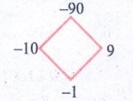
x² − x – 90 = x² − 10x + 9x − 90

= x (x − 10) + 9 (x − 10)

= (x + 9) (x − 10)

10. 9x² − 6x – 8

 9x² − 6x – 8 = 9x² − 12x + 6x − 8

= 3x (3x − 4) + 2(3x − 4)

= (3x + 2) (3x − 4)