Exercise 3.1 (Multiplication of Algebraic Expressions)

Exercise 3.1

1. Complete the table.

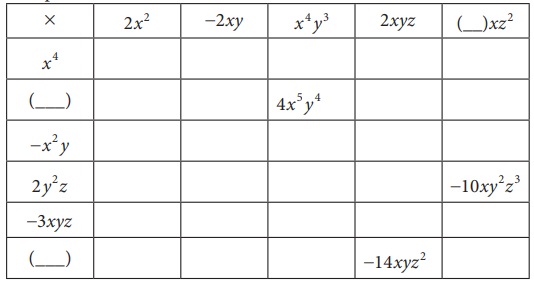
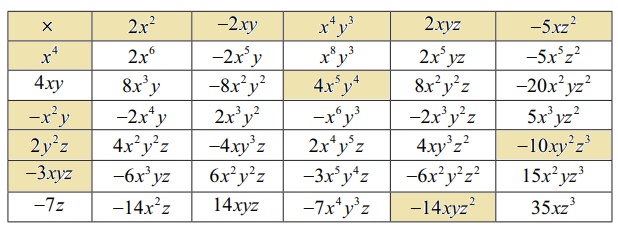
Solution:

2. Find the product of the terms.

(i) −2mn , (2m)² , −3mn (ii) 3x ² y , −3xy³ , x ² y²

Solution:

(i) (−2mn) × (2m)² × (−3mn) = (−2mn) × 2²m² × (−3mn) = (− 2mn) × 4m² × (− 3mn)

= (−) (+) (−) (2 × 4 × 3) (m × m² × m) (n × n)

= + 24 m⁴ n²

(ii) (3x²y) × (−3xy³) × (x²y²) = (+) × (−) × (+) × (3 × 3 × 1) (x² × x × x²) × (y × y³ × y² )

= −9x⁵y⁶

3. If l = 4 pq² , b = −3p²q , h = 2 p³ q³ then, find the value of l × b × h .

Solution:

Given l = 4pq²

b = −3p²q

h = 2p³q³

 l × b × h = (4pq²) × (−3p²q ) × (2p³q³)

= (+) (−) (+) (4 × 3 × 2) (p × p² × p³) (q² × q × q³)

= −24p⁶q⁶

4. Expand

(i) 5x (2 y − 3) 

(ii) −2 p(5p² − 3p + 7) 

(iii) 3mn(m³n³ − 5m²n + 7mn² ) 

(iv) x² (x + y + z) + y² (x + y + z) + z² (x − y − z)

(i) 5x (2y − 3)

5x (2y − 3) = (5x)(2y) − (5x)(3)

= (5 × 2)(x × y) − (5 × 3)x

= 10xy − 15x

(ii) −2p (5p² −3p + 7)

 −2p (5p² −3p + 7) = (−2p) (5p²) + (−2p) (−3p) + (−2p) (7)

= [(−) (+) (2 × 5) (p × p²)] + [(−) (−) (2 × 3) (p × p)] + (−)(+)(2 × 7) p

= −10p³ + 6p² − 14p

(iii) 3mn(m³n³ – 5m²n + 7 mn²)

 3mn(m³n³ – 5m² n + 7 mn²) = (3mn) (m³n³) + (3mn) (−5m²n) + (3mn)(7mn²)

= (3) (m × m³) (n × n³) + (+) (−) (3 × 5) (m × m²) (n × n) + (3 × 7) (m × m)(n × n²)

= 3m⁴ n⁴ − 15m³ n² + 21m²n³

(iv) x²(x + y + z) + y²(x + y + z) + z²(x –y − z)

 x² (x + y + z) + y² (x + y + z) + z²(x –y − z) = (x² × x) + (x² × y) + (x² × z ) + (y² × x) + (y² × y) + (y² × z) + (z^{2 ×} x) + z² (−y) + z² (−z)

= x³ + x²y + x²z + xy² + y³ + y²z + xz² − yz² − z³

= x³ + y³ − z³ + x²y + x²z + xy² + zy² + xz² − yz² 

5. Find the product of

(i) (2x + 3)(2x − 4) 

(ii) ( y² − 4)(2 y² + 3y)

(iii) (m² − n)(5m²n² − n² )

(iv) 3(x − 5) × 2(x −1)

Solution:

(i) (2x + 3) (2x − 4)

 (2x + 3) (2x − 4) = (2x) (2x − 4) + 3(2x − 4)

 = (2x × 2x) − 4(2x) + 3(2x) − 3(4)

 = 4x² − 8x + 6x − 12 = 4x² + (− 8 + 6)x − 12

 = 4x² − 2x – 12

(ii) (y² − 4) (2y² + 3y)

 (y² − 4) (2y² + 3y) = y²(2y² + 3y) – 4 (2y² + 37)

 = y² (2y²) + y²(3y) − 4(2y²) − 4(3y)

 = 2y⁴ + 3y³ − 8y² − 12y

(iii) (m² − n) (5m²n²− n²)

 (m² − n) (5m²n² − n²) = m² (5m²n² − n²) − n (5m²n² − n²)

 = m² (5m²n²) + m²(−n²) − n(5m²n²) + (−)(−)n(n²)

 = 5m²n² − m²n² − 5m²n³ + n³

(iv) 3(x − 5) × 2(x − 1)

3(x − 5) × 2(x − 1) = (3 × 2) (x − 5) (x − 1)

 = 6 × [x (x − 1) − 5 (x − 1)]

 = 6 [x.x − x . 1 − 5x + (−1) (−) 5 1 ]

 = 6 [x² − x − 5x + 5] = 6 [x² + (−1 −5)x + 5]

 = 6 [x² − 6x + 5] = 6x² − 36x + 30

6. Find the missing term

(i) 6xy × _________ = −12x³y 

(ii) _________× ( −15m²n³p) = 45m³n³p²

(iii) 2y (5x² y − ___+ 3 ___) = 10x²y² − 2xy + 6y³

Solution:

(i) 6xy × = (−2x² ) = −12x³y

(ii) −3mp  × (−15m²n³p) = 45m³n³p²

(iii) 2y(5x²y – x + 3y²) = 10x²y² − 2xy + 6y³

7. Match the following.

a) 4y² × −3y (i) 20x² y − 20x

b) −2xy(5x² − 3) (ii) 5x³ − 5xy² + 5x²y

c) 5x (x² − y² + xy) (iii) 4x² − 9

d) (2x + 3)(2x − 3) (iv) −12 y³

e) 5x (4xy − 4) (v) −10x³y + 6xy

A) iv, v, ii, i, iii

B) v, iv, iii, ii, i

C) iv, v, ii, iii, i

D) iv, v, iii, ii, i

[Answer C : (a)−iv, (b)−v, (c)−ii, (d)−iii, (e)−i]

8. A car moves at a uniform speed of ( x + 30) km/hr. Find the distance covered by the car in ( y + 2) hours. (Hint: distance = speed × time).

Solution:

Sppeed of the car = (x + 30) km / hr.

Time = (y + 2) hours

Distance = Speed × time

= (x + 30) (y + 2) = x(y + 2) + 30(y + 2)

= (x) (y) + (x) (2) + (30) (y) + (30) (2)

= xy + 2x + 30y + 60

Distance covered = (xy + 2x + 30y + 60) km

Objective Type Questions

9. The product of 7 p³ and (2 p²)² is

(A) 14 p¹²

(B) 28 p⁷

(C) 9 p⁷

(D) 11p¹²

[Answer: (B) 28 p⁷]

10. The missing terms in the product −3m³n × 9(__) = _________ m⁴n³ are

(A) mn² , 27

(B) m²n, 27

(C) m²n² , −27

(D) mn² , −27

[Answer: (A) mn², 27]

11. If the area of a square is 36x⁴ y² then, its side is ____________

(A) 6x ⁴ y²

(B) 8x ² y²

(C) 6x ² y

(D) −6x ² y

[Answer: (C) 6 x²y]

12. If the area of a rectangle is 48m²n³ and whose length is 8mn² then, its breadth is__.

(A) 6 mn

(B) 8m²n

(C) 7m²n²

(D) 6m²n²

[Answer: (A) 6mn]

13. If the area of a rectangular land is (a ² − b² ) sq.units whose breadth is (a − b) then, its length is__________

(A) a − b

(B) a + b

(C) a ² − b

(D) (a + b)²

[Answer: (B) a + b]

Answer:

Exercise 3.1

1. 

2. (i) 24m⁴ n²  (ii) − 9x⁵ y⁶

3. − 24 p ⁶ q⁶

4. (i) 10 xy −15x (ii) − 10 p ³ + 6 p² −14 p

(iii ) 3m⁴ n ⁴ − 15m³ n ² + 21m² n³

(iv) x³ + y³ − z³ + x²y + x²z + xy² + zy² + xz² − yz²

5. (i ) 4x² − 2 x −12

(ii) 2 y ⁴ + 3y³ − 8 y ² −12 y

(iii) 5m⁴ n² - m² n ² - 5m² n ³ + n³

(iv) 6x² - 36 x + 30

6. (i) − 2x² ii) − 3mp iii) y(5x ² y − x + 3y² )

7. (C) iv, v, ii, iii, i

8. xy + 2x + 30 y + 60

9. (B) 28p⁷

10. (D) mn², –27

11. (C) 6x² y

12. (A) 6 mn

13. (B) (a+b)