Algebra | Chapter 3 | 8th Maths - Factorisation using cubic identities | 8th Maths : Chapter 3 : Algebra
Chapter: 8th Maths : Chapter 3 : Algebra
Factorisation using cubic identities
Factorisation
using cubic identities
The cubic
identities are
(i) (a + b)3
=
a3 +
3a2b + 3ab2 +
b3
(ii) (a − b)3
=
a3 −
3a2b + 3ab2 −
b3
Note
8a 3 = 2 × 2 × 2 × a3
= 23 a3 = (2a)3
I. Factorise
using the identity (a + b)3 = a3 + 3a2b + 3ab2
+ b3
Example 3.26
Factorise:
x3 + 15x2 + 75x + 125
Solution:
x3 + 15x2 + 75x
+ 125
This can
be written as x3 + 15x2 + 75x + 53
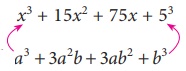
Comparing
with a 3 +
3a2b + 3ab 2 +
b3 = (a + b)3
we get a = x
, b = 5
The given
expression can be expressed as
(x)3 + 3(x)2 (5) + 3(x)
(5)2 + (5)3 = (x
+ 5)3
= (x + 5) (x + 5) (x + 5) are the three
factors.
Note
Perfect cube numbers
A number which can be written in the form of x × x × x is
called perfect cube number
Examples
8=2×2×2=23
27=3×3×3=33
125=5×5×5=53
Here 8, 27, 125 are some of perfect cube numbers
II. Factorise
using the identity (a – b)3 = a3 – 3a2b + 3ab2
– b3
Example 3.27
Factorise:
8p3 – 12p2q + 6pq2 – q3
Solution:
Given 8p3 – 12p2q + 6pq2 – q3
This can
be written as
(2p)3
– 12p2q + 6pq2 – (q)3
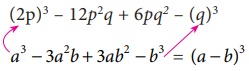
Comparing
this with a 3 −
3a2b + 3ab 2 −
b3 = (a − b)3 we get a = 2p ,
b = q
The given
expression can be expressed as
(2p)3
– 3(2p)2(q) + 3(2p)(q)2 – (q)3
= (2p –q)3
= (2p –q),
(2p –q), (2p –q) are the three factors.