Division of Algebraic Expressions

Division of Algebraic Expressions

In the previous sessions, we have learnt how to add, subtract and multiply algebraic expressions. Now, we are going to learn about another basic operation ‘division’ on algebraic expressions. We know that the division is the reverse operation of multiplication.

Now, the cost of 10 balls at the rate of ₹5 each = 10 × 5

= ₹50

whereas if we have ₹50 and we want to buy 10 balls then, the cost of each ball is

 = 50/10 = ₹5

What we have seen above is division on numbers. But how will you divide an algebraic expression by another algebraic expression?

Of course, the same procedure has to be followed for the algebraic expressions with the help of laws of exponents.

If x is a variable and m, n are constants, then x^m ÷ xⁿ = x^{m −n} where m > n .

1. Division of a monomial by another monomial

Dividing a monomial 10 p⁴ by another monomial 2p³, we get

 10p⁴ ÷ 2p³

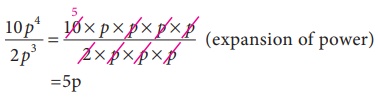
However, to divide we can also follow laws of exponents as,

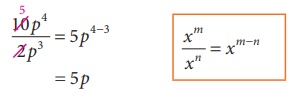
Think

Are the following correct?

(i) x³/x⁸ = x^8-3 = x⁵

(ii) 10m⁴ / 10m⁴ = 0

(iii) When a monomial is divided by itself, we will get 1?

Solution:

(i) x³ / x⁸ = x^{8 – 3} = x⁵

 x³ / x⁸ = x^{3 – 8} = x⁻⁵ (or) x³ / x⁸ = 1 / x^{8 – 3} = 1 / x⁵

∴  The given answer is wrong.

(ii) 10m⁴ / 10m⁴ = 0

10m⁴ / 10m⁴ = [10/10] m⁴⁻⁴ = 1 m⁰ = 1     [ ∵ m⁰ = 1]

∴  The given answer is not correct

(iii) When a monomial is divided by itself, we will get 1?

When a monomial is divided by itself, we will get 1.

Eg. x/x = x^{1 – 1} = x⁰ = 1

∴ The given statement is correct

Example 3.6

Velu pastes ‘4xy ’ pictures in one page of his scrap book. How many pages will he need to paste 100x² y³ pictures? (x, y are positive integers)

Solution:

Total number of pictures = 100x² y³

Pictures in one page = 4xy

Total number of pages needed = Total number of pictures / pictures in one page

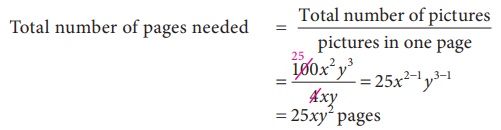
= 25xy² pages

Try these

Divide

(i) 12x ³y² by x²y (ii) −20a⁵b² by 2a³b⁷ (iii) 28a⁴ c² by 21ca²

(iv) (3 x ² y)³ √6x²y³ (v) 64m⁴ (n²)³ ÷ 4m²n² (vi) (8 x ² y ² )³ ÷ (8x ² y² )²

(vii) 81 p²q⁴ ÷ √[81p²q⁴ ]

(vii) ( 4x² y³ )⁰ ÷ [( x³)²]/x⁶

Solution:

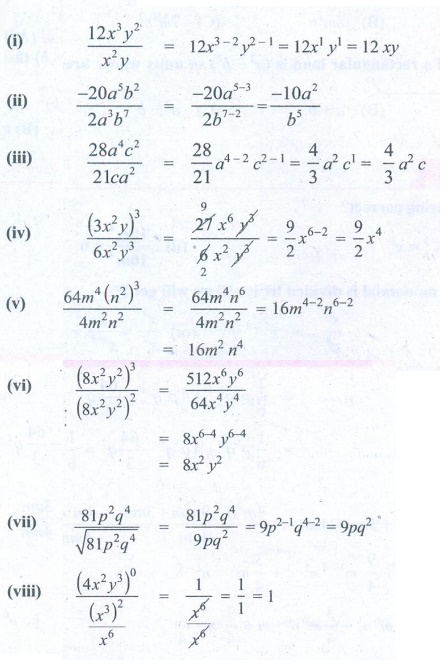
Solution:

(i) 12x³y² / x²y = 12x³⁻² y²⁻¹  = 12x¹y¹ = 12 xy

(ii) −20a⁵b² / 2a³b⁷ = −20a^{5 − 3} / 2b^{7 − 2}  = −10a² / b⁵

(iii) 28 a⁴c² / 21ca² = [28 / 21] a^{4 – 2} c^{2 – 1} = 4/3 a²c¹ = 4/3 a²c

(iv) (3x²y)³ / 6x²y³ = 27 x⁶y³ / 6 x²y³  = [9/2] x^6–2 = 9/2 x⁴

(v) 64m⁴(n²)³ / 4m²n² = 64m⁴n⁶ / 4m²n² = 16 m⁴⁻² n⁶⁻² = 16 m²n⁴

(vi) (8x²y²)³ / (8x²y²)² = 512 x⁶y⁶ / 64 x⁴y⁴

= 8x⁶⁻⁴ y⁶⁻⁴

= 8x²y²

(vii) 81p²q⁴ / √81p²q⁴ = 81p²q⁴ / 9pq² = 9 p²⁻¹q^4–2 = 9 pq²

(viii) (4x²y³)⁰ /  [ (x³)² / x⁶ ] = 1 / [ x⁶ / x⁶ ] = 1 / 1 = 1

2. Division of an algebraic expression (polynomial) by a monomial

To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.

Example 3.7

Divide : (5y³ − 25y² + 8 y) by 5y

Solution:

We have, (5y ³ − 25y² + 8 y ) ÷ 5y ₌ 5y ³ − 25y² + 8 y / 5y

= y ^{3 −1} − 5y^{2 −1} + 8/5 = y ² − 5y + 8/5

Think

Are the following divisions correct?

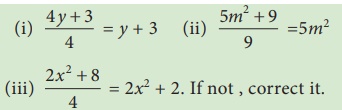
Solution:

(i) [4y + 3] / 4 = y + 3

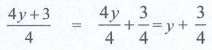
 [4y + 3] / 4 = [4y / 4] + [3 / 4] = y + [3/4] is the correct answer.

∴  The given answer is not correct.

(ii) [5m² + 9] / 9 = 5m²

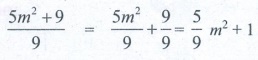
[5m² + 9] / 9 = [5m² / 9] + [9 / 9] = [ 5/9 m² ] + 1 is the correct answer

∴  The given answer is not correct.

(iii) [2x² + 8] / 4 = 2x² + 2 If not, correct it.

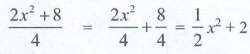
[2x² + 8] / 4 = [(2x²) / 4 ] + [ 8 / 4 ] = (1/2) x² + 2 is the correct answer

∴  The given answer is not correct.

Try these

(i) (16 y⁵ − 8y² ) ÷ 4 y

(ii) ( p⁵ q² + 24 p³ q −128q³ ) ÷ 6q

(iii) (4m²n + 9n²m + 3mn) ÷ 4mn

Solution:

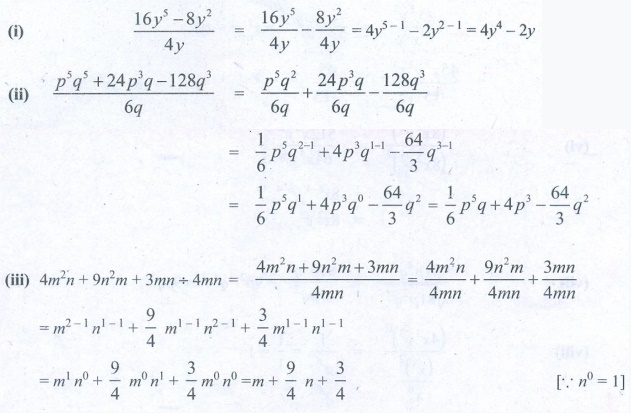
(i) (16y⁵ − 8y²) ÷ 4y

(16y⁵ − 8y²) / 4y = [16y⁵ / 4y ]− [ 8y² / 4y ] = 4y^{5 – 1} − 2y^{2 – 1} = 4y⁴ – 2y

(ii) ( p⁵q² + 24p³q − 128 q³ ) ÷ 6q

( p⁵q² + 24p³q − 128 q³ ) / 6q  = [ p⁵q² / 6q ] + [ 24p³q / 6q ] – [ 128q³ / 6q ]

= (1/6) p⁵q^{2 – 1} + 4p³q^{1 – 1} – (64/3)q^{3 – 1}

= (1/6)p⁵q¹ + 4p³q⁰ – (64/3)q² = (1/6)p⁵q + 4p³ – (64/3)q²

(iii) ( 4m²n + 9n²m + 3mn ) ÷ 4mn  

[ 4m²n + 9n² m + 3mn ] / 4mn = [ 4m²n / 4mn ] + [ 9n²m / 4mn ] + [ 3mn / 4mn ]

= m²⁻¹n¹⁻¹ + (9/4) m¹⁻¹n²⁻¹ + (3/4)m¹⁻¹n¹⁻¹

= m¹n⁰ + (9/4)m⁰ n¹ + (3/4)m⁰n⁰ = m + (9/4)n + 3/4.    [ ∵ n⁰ =1]