Word problems that involve linear equations

Word problems that involve linear equations

The challenging part of solving word problems is translating the statements into equations.

Collect as many such problems and attempt to solve them.

Example 3.33

The sum of two numbers is 36 and one number exceeds another by 8. Find the numbers.

Solution:

Let the smaller number be x and the greater number be x+8

Given: the sum of two numbers = 36

x + (x+8) = 36

2 x +8 = 36

2 x = 36 – 8

2 x = 28

x = 28/2 = 14

Hence,

(i) The smaller number, x =14

(ii) The greater number, x +8=14+8 = 22

Example 3.34

A bus is carrying 56 passengers with some people having ₹8 tickets and the remaining having ₹10 tickets. If the total money received from these passengers is ₹500, find the number of passengers with each type of tickets.

Solution:

Let the number of passengers having ₹8 tickets be y. Then, the number of passengers with ₹10 tickets is (56−y).

Total money received from the passengers = ₹500

That is, y × 8 + (56 - y) × 10 = 500

8y +560 −10y = 500

8y−10y = 500 – 560

− 2y = −60

y = 60/2

y = 30

Hence, the number of passengers having,

(i) ₹8 tickets =30

(ii) ₹10 tickets =56−30 =26

Example 3.35

The length of a rectangular field exceeds its breadth by 9 metres. If the perimeter of the field is 154m, find the length and breadth of the field.

Solution:

Let the breadth of the field be ‘x’ metres; then its length (x+9) metres.

Perimeter of the P = 2(length + breadth) = 2(x + 9 + x)= 2(2x + 9)

Given that, 2(2x + 9) = 154.

4x + 18 = 154

4x =154−18

4x = 136

x = 34

Hence,

(i) Thus, breadth of the rectangular field = 34m

(ii) length of the rectangular field = x+9 = 34+9 = 43m

Example 3.36

There is a wooden piece of length 2m. A carpenter wants to cut it into two pieces such that the first piece is 40 cm smaller than twice the other piece. What is the length of the smaller piece ?

Solution:

Let us assume that the length of the first piece is x cm.

Then the length of the second piece is (200cm – x cm) i.e., (200 − x) cm.

According to the given statement (change m to cm),

First piece = 40 less than twice the second piece.

x = 2× (200 − x) – 40

x = 400 − 2x – 40

x + 2x = 360

3x = 360

x = 360/3

x = 120

Hence,

(i) Thus the length of the first piece is 120 cm

(ii) The length of second piece is 200cm − 120cm = 80cm, which happens to be the smaller.

Think

Suppose we take the second piece to be x and the first piece to be (200 − x), how will the steps vary? Will the answer be different?

Solution:

Let 2^nd piece be ‘x’ & 1^st piece is 200 − x

Given that 1st piece is 40 cm smaller than hence the other piece

∴ 200 − x = 2 × x − 40

200 − x = 2x – 40 

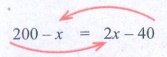
 ∴ 200 + 40 = 2x + x

240 = 3x

∴  x = 240 / 3 = 80

∴  1^st piece = 200 – x = 200 – 80 = 120 cm

2^nd piece = x = 80 cm

The answer will not change

Example 3.37

Mother is five times as old as her daughter. After 2 years, the mother will be four times as old as her daughter. What are their present ages?

Solution:

Given condition: After two years, Mother’s age = 4 times of Daughter's age

5 x + 2 = 4 ( x + 2)

5 x + 2 = 4 x + 8

5 x − 4x = 8 - 2

x = 6

Hence daughter’s present age = 6 years;

and mother’s present age = 5 x = 5 × 6 = 30 years

Example 3.38

The denominator of a fraction is 3 more than its numerator. If 2 is added to the numerator and 9 is added to the denominator, the fraction becomes 5/6. Find the original fraction.

Solution:

Let the original fraction be x/y.

Given that y = x + 3. (Denominator = Numerator + 3).

Therefore, the fraction can be written as x/(x + 3).

As per the given condition,

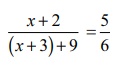
[(x + 2) ] / [(x + 3) + 9] = 5/ 6

By cross multiplication, 6( x +2) = 5 ( x +3+9)

6 x +12 = 5( x +12)

6 x +12 = 5 x +60

6x - 5x =60−12

x =60−12

x = 48.

x / x + 3 = 48 / 48+3 = 48/51

Therefore, the original fraction is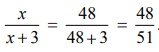 

Example 3.39

The sum of the digits of a two-digit number is 8. If 18 is added to the value of the number, its digits get reversed. Find the number.

Solution:

Let the two digit number be xy (i.e., ten’s digit is x, ones digit is y)

Its value can be expressed as 10x+y.

Given, x+y = 8 which gives y = 8 – x

Therefore its value is 10x+y

= 10x + 8 – x

= 9x + 8.

The new number is yx with value is 10y + x

= 10(8 − x) + x

= 80 – 9x

Given, when 18 is added to the given number (xy) gives new number (yx)

(9x + 8) + 18 = 80 – 9x

This simplifies to 9x + 9x = 80 –8–18

18x = 54

x = 3 ⇒ y = 8 – 3 = 5

The two digit number is xy = 10x+y ⇒ 10(3)+5 = 30+5 = 35

Example 3.40

From home, Rajan rides on his motorbike at 35 km/hr and reaches his office 5 minutes late. If he had ridden at 50 km/hr, he would have reached his office 4 minutes earlier. How far is his office from his home?

Solution:

Let the distance be ‘x’ km. (Recall that, time = Distance / Speed)

Time taken to cover ‘x’ km at 35 km/hr: T₁ = x/35 hr

Time taken to cover ‘x’ km at 50 km/hr: T₂ = x/50 hr

 Speed 1 = 35 km/hr

 Speed 2 = 50 km/hr

According to the problem, the difference between two timings

= 4–(–5)

= 4+5 =9 minutes

= 9/60 hour (changing minutes to hour)

Given, T₁ – T₂ = 9/60

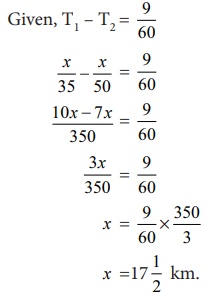
The distance to his office x = 17(1/2) km.