Exercise 3.9 (Graph)

Exercise 3.9

1. Fill in the blanks:

(i) y = p x where p ∈z always passes through the__________. [Answer: Origin (0, 0)]

Solution:

[When we substitute x = 0 in equation, y also becomes zero. ∴  (0, 0) is a solution]

(ii) The intersecting point of the line x = 4 and y = − 4 is__________. [Answer: 4, − 4]

Solution:

x = 4 is a line parallel to the y − axis and

y = − 4 is a line parallel to the x − axis. The point of intersection is a point that lies on both lines & which should satisfy both the equations. Therefore, that point is (4, −4)

(iii) Scale for the given graph ,

On the x-axis 1 cm = ------- units

y-axis 1 cm = ------- units

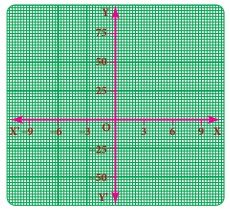
[Answer: 3 units, 25 units]

Solution:

 With reference to given graph,

On the x − axis, 1 cm = 3 units

y axis, 1cm =25 units

2. Say True or False.

(i) The points (1,1) (2,2) (3,3) lie on a same straight line. [Answer: True]

Solution:

The points (1, 1), (2, 2), (3, 3) all satisfy the equation y = x which is straight line. Hence, it is true

(ii) y =−9 x not passes through the origin. [Answer: False]

Solution:

y = −9x substituting for x as zero, we get y = − 9 × 0 = 0

∴  for x = 0, y = 0. Which means line passes through (0, 0), hence statement is false.

3. Will a line pass through (2, 2) if it intersects the axes at (2, 0) and (0, 2).

Solution:

Given a line intersects the axis at (2, 0) & (0, 2)

Let line intercept form be expressed as

ax + by = 1 Where a & b are the x & y intercept respectively.

Since the intercept points are (2, 0) & (0, 2)

a = 2, b = 2

∴ 2x + 2y = 1

When the point (2, 2) is considered & substituted in the equation

2x + 2y = 1 , we get

2 × 2 + 2 × 2 = 4 ≠ 1

∴ the point (2, 2) does not satisfy the equation. Therefore the line does not pass through (2, 2)

Alternatively graphical method

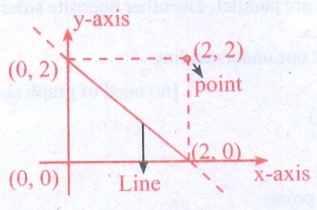
as we can see the line doesn’t pass through (2, 2)

4. A line passing through (4, −2) and intersects the Y-axis at (0, 2). Find a point on the line in the second quadrant.

Solution:

Line passes through (4, −2)

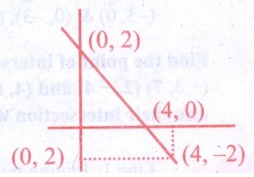
y – axis intercept point – (0, 2)

using 2 point formula,

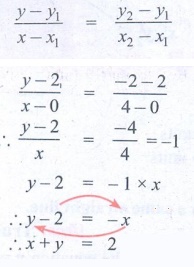
∴ x + y  = 2 is the equation of the line.

Any point in II quadrant will have x as negative & y as positive.

So let us take x value as − 2

∴  −2 + y = 2

∴  y = 2 + 2 = 4

∴  Point in II Quadrant is (−2, 4)

5. If the points P(5, 3) Q(−3, 3) R(−3, −4) and S form a rectangle, then find the coordinate of S.

Solution:

Plotting the points on a graph (approximately)

Steps :

1. Plot P, Q, R approximately on a graph.

2. As it is a rectangle, RS should be parallel to PQ & QR should be parallel to PS

3. S should lie on the straight line from R parallel to x−axis & straight line from P parallel to y−axis

4. Therefore, we get S to be (5, −4)

[Note: We don’t need graph sheet for approximate plotting. This is just for graphical understanding]

6. A line passes through (6, 0) and (0, 6) and an another line passes through (−3,0) and (0, −3). What are the points to be joined to get a trapezium?

Solution:

In a trapezium, there are 2 opposite sides that are parallel. The other opposite sides are non−parallel.

Now, let us approximately plot the points for our understanding

[no need of graph sheet]

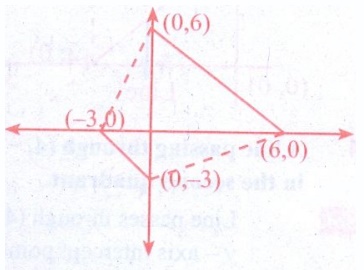
1. Plot the points (0, 6), (6, 0), (−3, 0) & (0, − 3)

2. Join (0, 6) & (6, 0)

3. Join (−3, 0) & (0, −3)

4. We find that the lines formed by joining the points are parallel lines.

5. So, for forming a trapezium, we should join (0, 6), (−3, 0) & (0, −3), (6, 0)

7. Find the point of intersection of the line joining points (−3, 7) (2, −4) and (4,6) (−5,−7). Also find the point of intersection of these lines and also their intersection with the axis.

Solution:

Line 1: Joining points (x_1, y₁) : (−3, 7) & ( x_2, y₂) : (2, −4) 

Equation of line joining 2 points by 2 point formula is given by

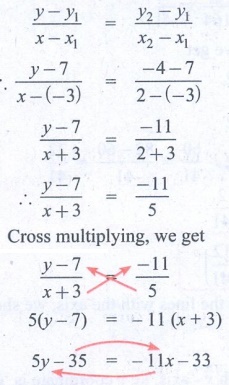
[y – y₁ ] / [ x – x₁ ] = [ y₂ – y₁ ] / [x₂ – x₁] ∴  [y – 7 ] / [x – (−3) ] = [−4 −7] / [2 – (−3)] ∴ [y – 7] / [x + 3] = −11 / [2 + 3] ∴[y – 7] / [x + 3] = −11 / [2 + 3]  ∴[ y – 7] / [x + 3] = −11 / 5

Cross multiplying, we get [y – 7] / [x + 3] = −11 / 5 ∴ 5(y − 7) = −11 (x + 3) ∴5y − 35 = − 11x – 33 

Transposing the variables, we get

11x + 5y = 35 − 33 = 2

11x + 5y = 2  Line 1

Similarly, we should find out equation of second line

Joining the points x₁ y₂ : (4, 6) & x₂ y₂ : (−5, −7)

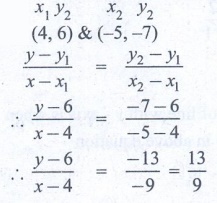
[y – y₁] /  [x – x₁] =  [y₂ – y₁] / [x₂ – x₁] ; ∴ [y − 6] / [x – 4] = [−7 – 6] / [− 5 − 4]

∴ [y − 6]  / [x – 4] = −13 / −9 = 13/9

∴ 9y − 54 = 13x − 52

∴ 9y −13x = 2  Line 2

For finding point of intersection, we need to solve the 2 line, equation to find a point that will satisfy both the line equations.

∴ Solving for x & y from line 1 & line 2 as below

11x + 5y = 2 ⇒ multiply both sides by 13,

11 × l3x + 5 × l3y = 26 ....(3)

Line 2: 9y − 13x = 2  ⇒  multiply both sides by 11

9 × 11y – 13 × 11x = 22 ....(4)

i.e  65y + 143x = 26 ....(3)

+ 99y − 143x = 22 ....(4)

Adding (3) & (4)

65y + 99y + 0 = 26 + 22   

∴ 164y = 48

∴ y = 48 / 164 = 12 / 41

Substituting this value of y in line 1 we get

11x + 5y = 2

11x + 5y × [12/41] = 2

11x = 2 – 60/41 = [82 – 60] / 41 = 22/41

∴  x = 22/41

∴  Point of intersection is (2/41, 12/41) 

To find point of intersection of the lines with the axis, we should substitute values & check

Line 1:      11x + 5y = 2

   Point of intersection of line with x− axis, i.e y coordinate is ‘0’

∴ Put y = 0 in above equation

∴ 11x – 5 × 0 = 2

∴ 11x + 0 = 2

∴ x = 2 / 11

∴  Point is (2/11, 0) 

Similarly, point of intersection of line with y − axis is when x −coordinate becomes ‘0’

∴ put x = 0 in above equation

∴ 11 × 0 + 5y = 2

∴ 0 + 5y = 2

y = 2/5

∴  Point is (0, 2/5) 

Similarly for line 2,

9y −13x = 2

For finding x intercept, i.e point where line meets x axis, we know thaty coordinate becomes ‘0’

∴ Substituting y = 0 in above eqn. we get

9 × 0 −13x = 2

∴ 0 − 13x = 2

∴ x = −2 / 13 

∴  Point : (− 2/13, 0) 

Similarly for y – intercept, x − coordinate becomes ‘0’

∴ Substituting for x = 0 in above equation. we get

9y – 13 × 0 = 2

9y − 0 = 2

9y = 2

y = 2 / 9

Point (0, 2/9) 

8. Draw the graph of the following equations, (i) x = −7 (ii) y = 6

Solution:

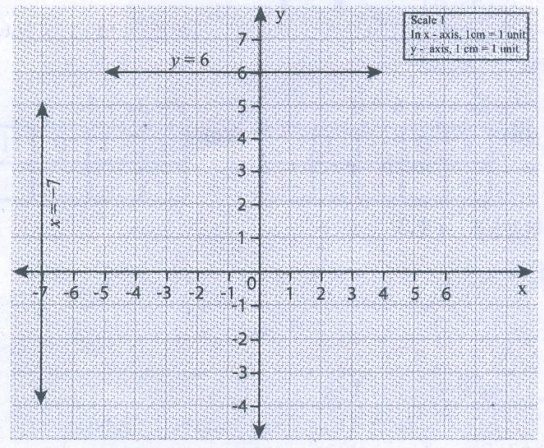
9. Draw the graph of (i) y = −3 x ii) y = x−4 iii) y = 2x+5

Solution:

To draw graph, we need to find out some points.

(i) y = − 3x

for y = − 3x, let us first substituting values & check

put x = 0

y = −3 × 0 = 0       ∴  (0, 0) is a point

put x = 1

y = −3 × l = −3    ∴  (1, −3) is a point

If join these 2 points, we will get the line

ii) y = x − 4

for y = x − 4

put x = 0

 y = 0 – 4 = − 4    ∴ (0, − 4) is a point

x = 4

y = 4 – 4 = 0    ∴  (4, 0) is a point

iii) y = 2x + 5

for y = 2x + 5

 put x = − 1

y = 2 (−1) + 5 = −2 + 5 = 3   ∴   (− 1, 3) is a point

put x = −2

y = 2 (−2) + 5 = − 4 + 5 = 1   ∴  (− 2, 1) is a point

Now let us plot the points & join them on graph

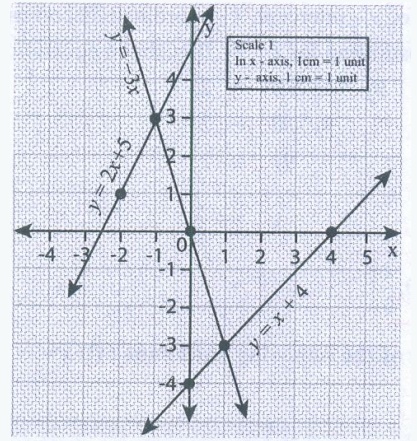
10. Find the values.

Solution:

(a)  Let y = x + 3

(i) if x = 0, y = 0 + 3 = 3,

  ∴   y = 3

(ii) y = 0, 0 = x + 3,

∴ x = − 3

(iii) x = − 2, y = −2 + 3

∴ y = 1

(iv) y = −3, − 3 = x + 3,

∴ x = − 6

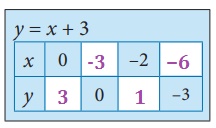
(b) Let 2x + y − 6 = 0

(i) x = 0, 2 × 0 + y − 6 = 0, y = 6

(ii) y = 0, 2x + 0 − 6 = 0,  ∴ 2x = 6

x = 3

(iii) x = − 1, 2 × (− l) + y − 6 = 0, − 8 + y = 0

y = 8

(iv) y = − 2, 2x − 2 − 6 = 0, 2x = 8

x = 4

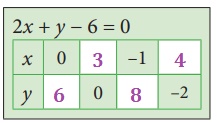
(c) Let y = 3x + 1

(i) x = −l, y = 3 (−1)+1 = 0, ∴ y = −2

(ii) x = 0, y = 3 (0) + 1 = 0, . ∴  y = l

(iii) x = 1, y = 3 (1) + 1 = 0, ∴ y = 4

(iv) x = 2, y = 3 (2) + 1 = 0,   ∴ y = 7

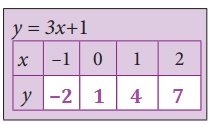
Exercise 3.9

1. (i) Origin (ii) (4,-4) (iii) x-axis 1cm=3 units, y-axis 1cm=25 units

2. (i) True (ii) False