Graph

Graph

1. Introduction

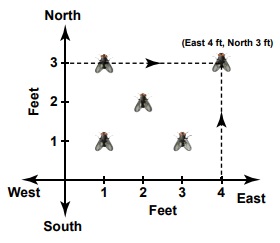
There was an instance in the 17^th century when Rene Descartes, a famous mathematician became ill and from his bed, noticed an insect hovering over a corner and sitting at various places on the ceiling. He wanted to identify all the places where the insect sat on the ceiling. Immediately, he drew the top plane of the room in a paper, creating the horizontal and vertical lines. Based on these perpendicular lines, he used the directions and understood that the places of the insect can be spotted by the movement of the insect in the east, west, north and south directions. He called that place as (x,y) in the plane which indicates two values, one (x) in the horizontal direction and the other (y) in the vertical direction (say east and north in this case). This is how the concept of graphs came into existence.

2. Graph sheets

Graph is just a visual method for showing relationships between numbers. In the previous class, we studied how to represent integers on a number line horizontally. Now take one more number line – vertically. We take the graph sheet keeping both number lines mutually perpendicular to each other at ‘0’zero as given in the figure. The number lines and the marking integers should be placed along the dark lines of the graph sheet.

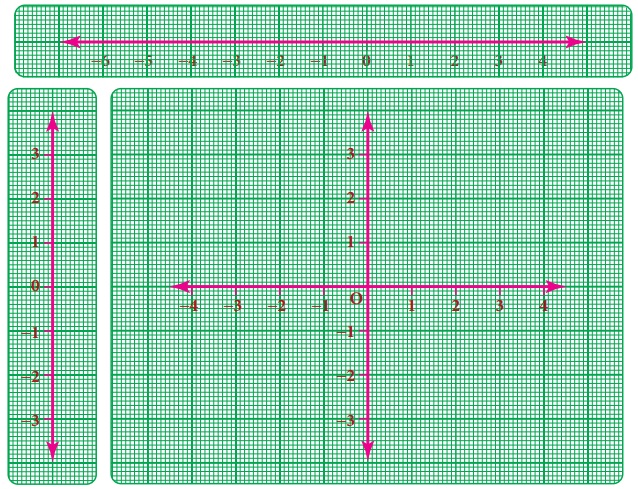
The intersecting point of the perpendicular lines ‘O’ represent the origin (0, 0).

Cartesian system

Rene Descartes system of fixing a point with the help of two measurements, horizontal and vertical, is named as Cartesian system, in his honour. The horizontal line is named as XOX^', called the X-axis. The vertical line is named as YOY', called the Y- axis. Both the axes are called coordinate axes. The plane containing the X axis and the Y axis is known as the coordinate plane or the Cartesian plane.

3. Signs in the graphs

1. X-coordinate of a point is positive along OX and negative along OX'

2. Y-coordinate of a point is positive along OY and negative along OY'

4. Ordered pairs

A point represents a position in a plane. A point is denoted by a pair (a,b) of two numbers ‘a’ and ‘b’ listed in a specific order in which ‘a’ represents the distance along the X-axis and ‘b’ represents the distance along the Y-axis. It is called an ordered pair (a,b). It helps us to locate precisely a point in the plane. Each point can be exactly identified by a pair of numbers. It is also clear that the point (b,a) is not same as (a,b) as they both indicate different orders.

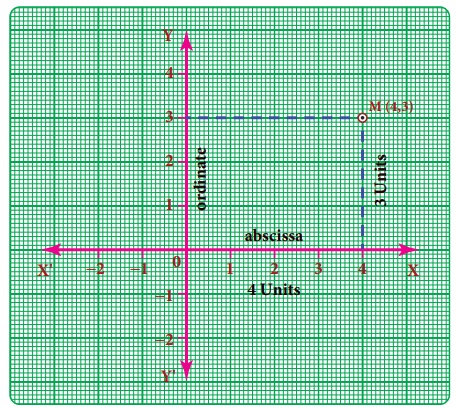
We have, XOX' and YOY' as the co-ordinate axes and let ‘M’ be (4,3) in the plane.To locate ‘M’

(i) you (always) start at O, a fixed point (which we have, agreed to call as origin),

(ii) first, move 4 units along the horizontal direction (that is, the direction of x-axis)

(iii) and then trek along the y- direction by 3 units.

To understand how we have travelled to reach M, we denote by (4,3).

4 is called the x-coordinate of M and 3 is called the y-coordinate of M. It is also habitual to name the x-coordinate as abscissa and the y-coordinate as ordinate. (4,3) is as an ordered pair.

Think

If instead of (4,3), we write (3,4) and try to mark it, will it represent ‘M’ again?

Solution:

Let 3, 4 be M, when we mark, we find that it is a different point and not ‘M’

5. Quadrants

The coordinate axes divide the plane of the graph into four regions called quadrants. It is a convention that the quadrants are named in the anti clock wise sense starting from the positive side of the X axis.

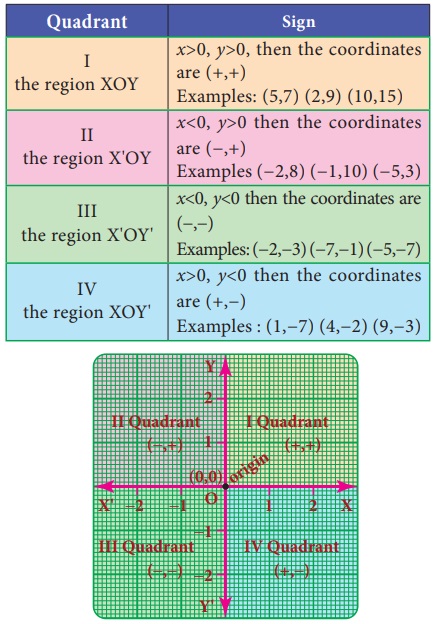
Quadrant : Sign:

Quadrant : I the region XOY : Sign: x>0, y>0, then the coordinates are (+,+) Examples: (5,7) (2,9) (10,15)

Quadrant : II the region X'OY : Sign: x<0, y>0 then the coordinates are (−,+) Examples (−2,8) (−1,10) (−5,3)

Quadrant : III the region X'OY' : Sign: x<0, y<0 then the coordinates are (−,−) Examples: (−2,−3) (−7,−1) (−5,−7)

Quadrant : IV the region XOY' : Sign: x>0, y<0 then the coordinates are (+,−) Examples : (1,−7) (4,−2) (9,−3)

Coordinate of a point on the axes:

•If y=0 then the coordinate (x, 0) lies on the ‘x’-axis.

For example (2, 0) (−5, 0) (7,0) are points on the ‘x’-axis.

•If x=0 then the coordinate (0,y) lies on the ‘y’-axis.

For example (0, 3) (0,−4) (0, 9) are points on the ‘y’-axis.

6. Plotting the given points on a graph

Consider the following points (4,3), (−4,5), (−3,−6), (5,−2), (6,0), (0,−5)

(i) To locate (4,3).

Start from origin O, move 4 units along OX and from 4, move 3 units parallel to OY to reach M(4,3).

(ii) To locate (−4,5)

From the origin, move 4 units along OX' and from −4, move 5 units parallel to OY to reach N(−4,5).

(iii) To locate (-3, -6)

From the origin move 3units along OX' and from −3, move 6 units parallel to OY' to reach P(-3,-6).

(iv) To locate (5,−2)

From the origin move 5 points along OX and from 5, move 2 units parallel to OY' to reach Q(5,−2).

(v) To locate (6,0) and (0, 5)

In the given point (6, 0), X-coordinate is 6 and Y-coordinate is zero. So the point lies on the x-axis. Move 6 units on OX from the origin to reach R(6, 0).

In the given point (0,−5) X-coordinate is zero and Y- coordinate is (−5). So, the point lies on Y-axis. Move 5 units on OY' from the origin to reach S (0,−5).

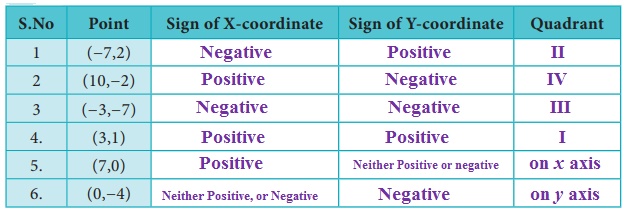
Try these

1. Complete the table given below.

2. Write the coordinates of the points marked in the following figure

Solution:

A- (−3, 2) B - (5, 2) C- (5, −3) D - (−3, 3) E - (−l, 4)

F- (l, 2) G - (7, 4) H - (0, 2) I - (0, 3) J - (−3, 0)

K-(5, 0) L - (−l, 0) M - (−2, 0) N- (−2, −1) O - (0, 0)

P - (−1, −1) Q - (1, −1) R - (2, −l) S - (0, −3) T- (7, 0)

U - (7, −2)